Leetcode：98. 验证二叉搜索树（C++）

news2024/11/24 9:33:51

问题描述：

实现代码与解析：

递归：

原理思路：

迭代（中序）：

思路原理：

问题描述：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

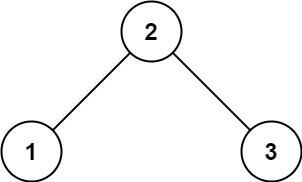
输入：root = [2,1,3]
输出：true

示例 2：

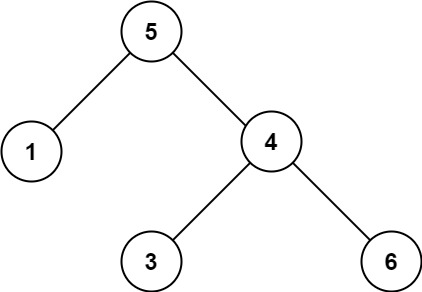
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

实现代码与解析：

递归：

class Solution {
public:
    void traversal(TreeNode* root,vector<int>& vec)
    {
        if(root==NULL) return;
        traversal(root->left,vec);
        vec.push_back(root->val);//中序
        traversal(root->right,vec);

    }
    bool isValidBST(TreeNode* root) 
    {
        vector<int> vec;
        traversal(root,vec);
        for(int i=1;i<vec.size();i++)
        {
            //搜索树种也不能有相同元素，所以有等于号
            if(vec[i-1]>=vec[i]) return false; 
        }
        return true;
    }
};

原理思路：

根据二叉搜索树的性质，我们中序遍历转化出来的数组一定是单调递增的且没有重复元素，代码是很好写出的。

当然也可以不用数组，直接在递归时判断出来是否有序。下面给出代码：

class Solution {
public:
    long max=LONG_MIN;
    bool isValidBST(TreeNode* root) 
    {
       if(root==NULL) return true;
       bool left=isValidBST(root->left);
       if(root->val>max) max=root->val;//更新最大值
       else return false;//若不递增，不用再向右遍历了直接返回false
       bool right=isValidBST(root->right);
       return left&&right;
    }
};

这题测试数据中有INT_MIN，所以这里我们用LONG_MIN，当然如果这里测试数据有最小的LLONG_MIN，无法找出比它还小的值，那我们就换一种方式来比较，记录前一个结点值来判断即可：

class Solution {
public:
    TreeNode* pre = NULL; // 用来记录前一个节点
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        bool left = isValidBST(root->left);
        //当pre不为空
        if (pre != NULL && pre->val >= root->val) return false;
        pre = root; //记录前一个结点
        bool right = isValidBST(root->right);
        return left && right;
    }
};

其实第一次看这个题，我想的是比较左右子树与根结点的值大小来判断返回，就像这样：

if(root->val<=root->left->val||root->val>=root->right->val) return false;

后来发现，其实这样是错误的，这样只判断左右子树的根节点，而二叉搜索树是左子树所有结点都小于根结点，右子树的所有结点都大于根节点，所以不能这样写。

迭代（中序）：

class Solution {
public:
    bool isValidBST(TreeNode* root) 
    {
        stack<TreeNode*> st;
        TreeNode* pre=NULL;
        while(root!=NULL||!st.empty())
        {
            if(root!=NULL)
            {
                st.push(root);
                root=root->left;
            }
            else
            {
                root=st.top();
                st.pop();
                if(pre!=NULL&&root->val<=pre->val) return false;
                pre=root;//保存结点
                root=root->right;
            }
        }
        return true;
    }
};