LeetCode-322. 零钱兑换【广度优先搜索数组动态规划】

news2024/10/7 6:46:55

LeetCode-322. 零钱兑换【广度优先搜索数组动态规划】

题目描述：
解题思路一：Python动态规划五部曲：定推初遍举【先遍历物品后遍历背包】
解题思路二：Python动态规划五部曲：定推初遍举【先遍历背包后遍历物品】
解题思路三：0

题目描述：

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1
示例 2：

输入：coins = [2], amount = 3
输出：-1
示例 3：

输入：coins = [1], amount = 0
输出：0

提示：

1 <= coins.length <= 12
1 <= coins[i] <= 2³¹ - 1
0 <= amount <= 10⁴

解题思路一：Python动态规划五部曲：定推初遍举【先遍历物品后遍历背包】

确定dp数组以及下标的含义
dp[j]：凑足总额为j所需钱币的最少个数为dp[j]
确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）

所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。

递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;

其他下标对应的数值呢？

考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。

所以下标非0的元素都是应该是最大值。

确定遍历顺序
本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。

所以本题并不强调集合是组合还是排列。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

在动态规划专题我们讲过了求组合数是动态规划：518.零钱兑换II (opens new window)，求排列数是动态规划：377. 组合总和 Ⅳ (opens new window)。

所以本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的！

那么我采用coins放在外循环，target在内循环的方式。

本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序

综上所述，遍历顺序为：coins（物品）放在外循环，target（背包）在内循环。且内循环正序。

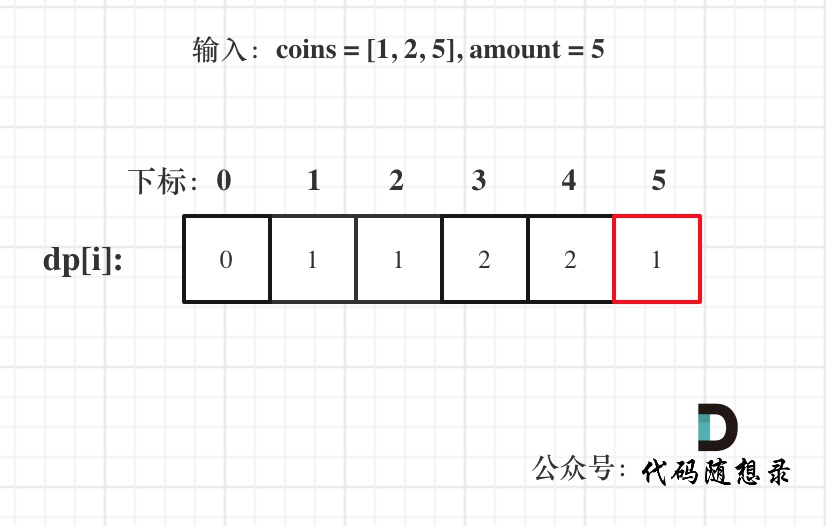
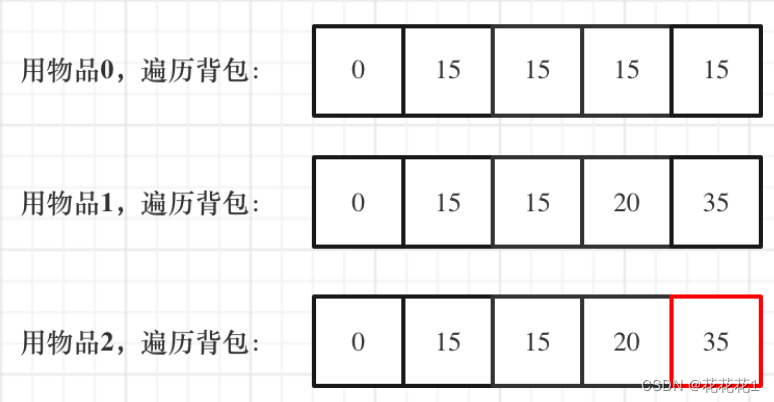
举例推导dp数组
以输入：coins = [1, 2, 5], amount = 5为例

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1) # 最终需要dp[amount]
        dp[0] = 0
        for coin in coins:
            for j in range(coin, amount + 1):
                dp[j] = min(dp[j], dp[j-coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1

时间复杂度：O(n)
空间复杂度：O(n)

解题思路二：Python动态规划五部曲：定推初遍举【先遍历背包后遍历物品】

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0

        for i in range(1, amount + 1):  # 遍历背包容量
            for coin in coins:  # 遍历物品
                if i - coin >= 0:
                    # 更新凑成金额 i 所需的最少硬币数量
                    dp[i] = min(dp[i], dp[i - coin] + 1)

        return dp[amount] if dp[amount] != float('inf') else -1