目录
- 题目描述
- 思路及实现
- 方式一:动态规划法
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- 复杂度分析
- 方式二:中心扩展法
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- 复杂度分析
- 总结
- 相似题目
- 标签(题目类型):回文串、动态规划
题目描述
给定一个字符串 `s`,找到其中最长的回文子串。可以假设 `s` 的最大长度为 1000。
示例1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例2:
输入: "cbbd"
输出: "bb"
原题:LeetCode 5
思路及实现
方式一:动态规划法
思路
Dynamic Programming(DP) 动态规划是一种将问题分解成子问题并分别计算的优化技术。对于回文子串,我们可以使用动态规划来解决。
对于一个子串而言,如果它是回文串,并且长度大于 2,那么将它首尾的两个字母去除之后,它仍然是个回文串。例如对于字符串 “ababa”,如果我们已经知道 “bab” 是回文串,那么 “ababa” 一定是回文串,这是因为它的首尾两个字母都是 “a”。
通过定义一个二维数组 dp[i][j],表示 s 的第 i 个字符到第 j 个字符组成的子串是否为回文字符串。当 i == j 时,表示一个字符,是回文字符串,当 i + 1 == j ,则优先考虑两个字符是否相等来将问题规模缩小,同时考虑前一个子串是否为回文字符串。对于 i + 1 < j 的情况,可以通过判断 s[i] 和 s[j] 是否相等,并判断定义的 dp[i+1][j-1] 是否为回文字符串。如果是回文字符串,则 dp[i][j] 也是回文字符串。
代码实现
Java版本
class Solution {
public String longestPalindrome(String s) {
int n = s.length(); // 计算字符串的长度
boolean[][] dp = new boolean[n][n]; // 创建一个二维数组用于记录子串是否为回文串
String ans = ""; // 初始化最长回文子串为空字符串
// 遍历所有长度的子串
for (int len = 1; len <= n; len++) {
// 遍历子串的起始位置
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1; // 子串的结束位置
if (len == 1) {
dp[i][j] = true; // 单个字符必定是回文串
} else if (len == 2) {
dp[i][j] = (s.charAt(i) == s.charAt(j)); // 只有两个字符时判断是否相等
} else {
dp[i][j] = (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]); // 多于两个字符时判断首尾字符是否相等
}
if (dp[i][j] && len > ans.length()) { // 如果当前子串是回文串并且长度更长
ans = s.substring(i, j + 1); // 更新结果为当前子串
}
}
}
return ans;
}
}
说明:
longestPalindrome 方法用于寻找给定字符串中的最长回文子串。使用动态规划的思想,创建一个二维数组 dp,其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否为回文串。
通过遍历所有长度的子串,以及遍历子串的起始位置,判断子串是否为回文串,并根据回文串的长度更新最长回文子串 ans。
当子串的长度为 1 时,即一个字符,必定是回文串。
当子串的长度为 2 时,判断首尾两个字符是否相等。
当子串的长度大于 2 时,判断首尾两个字符是否相等,并根据 dp[i+1][j-1] 的结果判断子串是否为回文串。
如果当前子串是回文串,并且长度比之前记录的最长回文子串长度更长,则更新最长回文子串 ans。
最后,返回最长回文子串。
C语言版本
char* longestPalindrome(char* s) {
int n = strlen(s); // 计算字符串的长度
bool dp[n][n]; // 创建一个二维数组用于记录子串是否为回文串
memset(dp, false, sizeof(dp)); // 初始化dp数组为false
char* ans = ""; // 初始化最长回文子串为空字符串
// 遍历所有长度的子串
for (int len = 1; len <= n; len++) {
// 遍历子串的起始位置
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1; // 子串的结束位置
if (len == 1) {
dp[i][j] = true; // 单个字符必定是回文串
} else if (len == 2) {
dp[i][j] = (s[i] == s[j]); // 只有两个字符时判断是否相等
} else {
dp[i][j] = (s[i] == s[j] && dp[i + 1][j - 1]); // 多于两个字符时判断首尾字符是否相等
}
if (dp[i][j] && len > strlen(ans)) { // 如果当前子串是回文串并且长度更长
char* sub = (char*)malloc((len + 1) * sizeof(char)); // 分配内存保存当前子串
strncpy(sub, s + i, len); // 复制当前子串到内存中
sub[len] = '\0'; // 添加字符串结束标志
ans = sub; // 更新结果为当前子串
}
}
}
return ans;
}
说明: (同上)
longestPalindrome 函数用于寻找给定字符串中的最长回文子串。使用动态规划的思想,创建一个二维数组 dp,用于记录子串是否为回文串。
通过遍历所有长度的子串,以及遍历子串的起始位置,判断子串是否为回文串,并根据回文串的长度更新最长回文子串 ans。
子串的判断分三种情况:
当子串的长度为 1 时,即一个字符,必定是回文串。
当子串的长度为 2 时,判断首尾两个字符是否相等。
当子串的长度大于 2 时,判断首尾两个字符是否相等,并根据 dp[i+1][j-1] 的结果判断子串是否为回文串。
如果当前子串是回文串,并且长度比之前记录的最长回文子串长度更长,则更新最长回文子串 ans。
最后,返回最长回文子串。
Python3版本
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
dp = [[False] * n for _ in range(n)]
ans = ""
# 遍历所有长度的子串
for length in range(1, n + 1):
# 遍历子串的起始位置
for i in range(n - length + 1):
j = i + length - 1 # 子串的结束位置
if length == 1:
dp[i][j] = True # 单个字符必定是回文串
elif length == 2:
dp[i][j] = (s[i] == s[j]) # 只有两个字符时判断是否相等
else:
dp[i][j] = (s[i] == s[j] and dp[i + 1][j - 1]) # 多于两个字符时判断首尾字符是否相等
if dp[i][j] and length > len(ans): # 如果当前子串是回文串并且长度更长
ans = s[i:j + 1] # 更新结果为当前子串
return ans
说明: (同上)
longestPalindrome 方法用于寻找给定字符串中的最长回文子串。使用动态规划的思想,创建一个二维数组dp,其中dp[i][j]表示从索引i到索引j的子串是否为回文串。通过遍历所有长度的子串,从最短的子串起,依次判断是否为回文串,并根据判断结果更新最长回文子串。最后,返回最长回文子串。
dp[i][j]的判断依据如下:
当子串长度为1时,dp[i][j]为True,因为单个字符必定是回文串;
当子串长度为2时,子串为回文串的条件是s[i]和s[j]相等;
当子串长度大于2时,子串为回文串的条件是首尾字符相等且去除首尾字符的子串也为回文串。
当发现一个更长的回文子串时,将其更新为结果。
复杂度分析
- 时间复杂度:该算法的时间复杂度为 O(n^2),其中 n 是字符串的长度。双重循环遍历了所有长度为 1 到 n 的子串。
- 空间复杂度:该算法的空间复杂度为 O(n^2),存储了一个二维数组 dp。
方式二:中心扩展法
思路
中心扩展法的基本思路是从左至右遍历字符串,以当前字符和其相邻字符为中心,向两边扩展,判断是否为回文串。在判断时,可以将回文串的起始和结束位置保存下来。
从每一个位置出发,向两边扩散即可。遇到不是回文的时候结束。举个例子,str=acdbbdaa 我们需要寻找从第一个 b(位置为 3)出发最长回文串为多少。怎么寻找?
首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
最后左右双向扩散,直到左和右不相等。如下图所示:
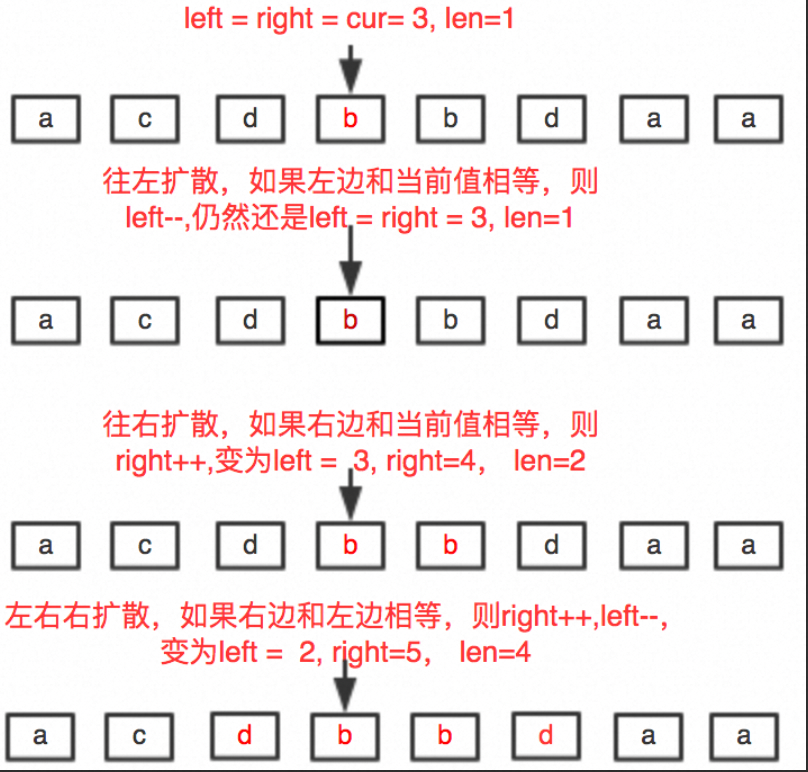
每个位置向两边扩散都会出现一个窗口大小(len)。如果 len>maxLen(用来表示最长回文串的长度)。则更新 maxLen 的值。
因为我们最后要返回的是具体子串,而不是长度,因此,还需要记录一下 maxLen 时的起始位置(maxStart),即此时还要 maxStart=len。
代码实现
Java版本
class Solution {
public String longestPalindrome(String s) {
int start = 0; // 回文串的起始位置
int end = 0; // 回文串的结束位置
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i); // 以当前字符为中心的回文串长度
int len2 = expandAroundCenter(s, i, i + 1); // 以当前字符和下一个字符为中心的回文串长度
int len = Math.max(len1, len2); // 取较长的回文串长度
if (len > end - start) {
start = i - (len - 1) / 2; // 更新回文串的起始位置
end = i + len / 2; // 更新回文串的结束位置
}
}
return s.substring(start, end + 1); // 根据起始位置和结束位置返回最长回文子串
}
private int expandAroundCenter(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--; // 向左扩展
right++; // 向右扩展
}
return right - left - 1; // 返回回文串的长度
}
}
说明:
longestPalindrome 方法用于寻找给定字符串中的最长回文子串。根据中心扩展法的思想,遍历字符串中的每个字符,以当前字符为中心向两边扩展,同时以当前字符和下一个字符为中心向两边扩展,获取回文串的长度。通过比较回文串的长度,不断更新最长回文串的起始位置和结束位置。最后,根据起始位置和结束位置从原字符串中截取出最长回文子串并返回。
expandAroundCenter 方法用于以指定的左右位置为中心向两边扩展,判断是否为回文串。通过比较左右位置的字符是否相等,并同时向左和向右移动位置来不断扩展回文串的长度。最后,返回回文串的长度。
C语言版本
char* longestPalindrome(char* s) {
int len = strlen(s);
int start = 0;
int end = 0;
for (int i = 0; i < len; i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = len1 > len2 ? len1 : len2;
if (len > end - start) {
start = i - (len - 1) / 2; // 更新回文串起始位置
end = i + len / 2; // 更新回文串结束位置
}
}
char *longest_palindrome = malloc((end - start + 2) * sizeof(char));
strncpy(longest_palindrome, s + start, end - start + 1); // 复制回文串至新分配的内存
longest_palindrome[end - start + 1] = '\0';
return longest_palindrome;
}
int expandAroundCenter(char *s, int left, int right) {
while (left >= 0 && right < strlen(s) && s[left] == s[right]) {
left--; // 向左扩展
right++; // 向右扩展
}
return right - left - 1; // 返回回文串的长度
}
说明:
longestPalindrome 函数用于寻找给定字符串中的最长回文子串。通过遍历字符串并以每个字符为中心依次判断以该字符或相邻两个字符为中心的回文串长度。通过比较回文串的长度,不断更新最长回文串的起始位置和结束位置。最后,将最长回文串从原字符串复制到新分配的内存中并返回。
expandAroundCenter 函数用于在给定字符串中以指定的左右位置为中心向两边扩展,判断是否为回文串。通过比较左右位置的字符是否相等,并同时向左和向右移动位置来不断扩展回文串的长度。最后,返回回文串的长度。
Python3版本
class Solution:
def longestPalindrome(self, s: str) -> str:
start = 0
end = 0
for i in range(len(s)):
len1 = self.expandAroundCenter(s, i, i)
len2 = self.expandAroundCenter(s, i, i + 1)
length = max(len1, len2)
if length > end - start:
start = i - (length - 1) // 2 # 更新回文串起始位置
end = i + length // 2 # 更新回文串结束位置
return s[start: end + 1] # 根据起始位置和结束位置返回最长回文子串
def expandAroundCenter(self, s: str, left: int, right: int) -> int:
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1 # 向左扩展
right += 1 # 向右扩展
return right - left - 1 # 返回回文串的长度
}
说明:
longestPalindrome 函数用于寻找给定字符串中的最长回文子串。通过遍历字符串并以每个字符为中心或相邻两个字符为中心依次判断以该中心为起点的回文串长度。通过比较回文串的长度,不断更新最长回文串的起始位置和结束位置。最后,根据起始位置和结束位置从原字符串中截取出最长回文子串并返回。
expandAroundCenter 函数用于在给定字符串中以指定的左右位置为中心向两边扩展,判断是否为回文串。通过比较左右位置的字符是否相等,并同时向左和向右移动位置来不断扩展回文串的长度。最后,返回回文串的长度。
复杂度分析
- 时间复杂度:该算法的时间复杂度为 O(n^2),其中 n 是字符串的长度。在中心扩展法中,每个字符仅遍历一次。
- 空间复杂度:该算法的空间复杂度为 O(1),只使用了常量级的额外空间。
总结
| 方式 | 备注 | 优点 | 缺点 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|---|---|
| 动态规划法 | 通过动态规划计算回文子串 | 算法稳定可靠 | 需要额外的二维数组存储状态 | O(n^2) | O(n^2) |
| 中心扩展法 | 通过扩展中心位置计算回文子串 | 具有较高效率 | 对空间的使用较低 | O(n^2) | O(1) |
相似题目
(表格形式,列举出)
| 相似题目 | 难度 | 链接 |
|---|---|---|
| 两个数组的交集 | 简单 | leetcode-349 |