一、 实验目的
1.加深学生对算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;
2.提高学生利用课堂所学知识解决实际问题的能力;
3.提高学生综合应用所学知识解决实际问题的能力。
二、实验任务
用动态规划算法实现:
1、矩阵链连乘问题  2、 投资问题
2、 投资问题 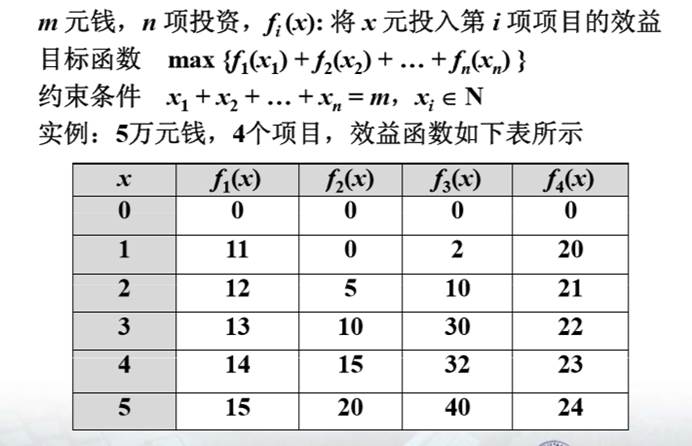 3、求解完全背包问题
3、求解完全背包问题
问题描述:有n种重量和价值分别为wi、vi(1≤i≤n)的物品,从这些物品中挑选总重量不超过W的物品,求出挑选物品价值总和最大的挑选方案,这里每种物品可以挑选任意多件。
4、旅行商问题
旅行商问题(TSP)又称旅行推销员问题、货郎担问题,它是数学领域中的著名问题之一。假设有一个旅行商人要访问n个城市,这n个城市是一个完全图。他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径选择目标是使求得的路径长度为所有路径之和中的最小值。
5、数字三角形 
问题描述:在上面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。
三、实验设备及编程开发工具
实验设备:Win10 电脑
开发工具:Visual Studio 2019
编程语言:C/JAVA
四、实验过程设计(算法设计过程)
(一)、矩阵连乘问题
1、算法分析:
(1寻找一个最优子结构。
对于原问题,我们使用表示乘积的结果矩阵,如果我们将在处进行一次括号划分,假设将其划分为和两部分,则=++(两个划分矩阵合并的代价)。假设这样划分是最优的,则只需继续在和上继续取到最佳划分即可。
(2递归定义最优解的值
在原问题中,我们定义数组m[i][j]表示计算矩阵所需乘法的最小值,则原问题计算所需最小代价为m[1][n]。
如果k表示矩阵i到j之间的划分点,那么m数组的公式为:
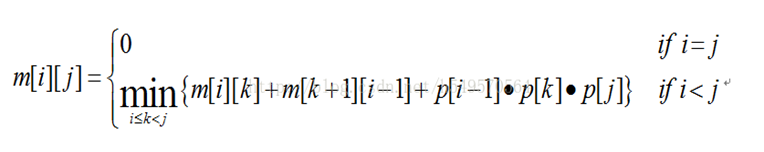
(3)计算最优代价
如果直接递归计算的话,我们会发现计算量仍然会很大,并没有明显改善。因此在这里,我们使用自底向上的方法进行计算,并且在计算中保存已经计算过的值,这样当上一层划分计算时,直接调用下层之前计算保存过的值即可。
在这整个过程中,我们使用m[i][j]从矩阵i到j的最小代价,用s[i][j]保存最小代价时的划分位置。根据2步骤的公式,我们只需按链条长度递增的顺序进行求解即可。在这里,它的长度是从2到n的(长度为1时直接为0)。由于只知道链的长度,因此有多个乘法问题,因此我们需要求解出所有乘法问题的最小代价。
2、代码实现:
#include<stdio.h>
#include<string.h>
#define N 1000
int m[N][N]; //m[i][j]表示从第i个矩阵乘到第j个矩阵所需的最小代价
int s[N][N]; //s[i][j]表示最优值m[i][j]对应的分割点
int p[N]; //p[]代表矩阵链,其中p0、p1为第一个矩阵的行和列
//对矩阵链p求解最佳组合方法,传入矩阵链和元素个数
void MATRIX_CHAIN_ORDER(int p[], int n) {
for(int i = 1; i <= n; i++) m[i][i] = 0; //子问题链长为1,代价为0
//对子问题链长2到n从小到大求出代价
for(int length = 2; length <= n; length++) {
for(int i = 1; i <= n-length+1; i++) {
int j = i+length-1;
m[i][j] = 999999; //初试值为一个很大的数
//此时求出从i到j的最小代价m[i][j]=min{m[i][k]+m[k+1][j]+Pi-1*Pk*Pj}
for(int k = i; k <= j-1; k++) {
if(m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j] < m[i][j]){
m[i][j] = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
s[i][j] = k;
}
}
}
}
}
//利用表s输出从start乘到ends的最优方案
void PRINT_OPTIMAL_PARENS(int s[][N], int start, int ends) {
if(start == ends) printf("A[%d]", start);
else {
printf("(");
PRINT_OPTIMAL_PARENS(s, start, s[start][ends]);
PRINT_OPTIMAL_PARENS(s, s[start][ends]+1, ends);
printf(")");
}
}
int main() {
int number;
printf("请输入待乘矩阵的个数:\n");
scanf("%d",&number);
memset(m, 0, sizeof(m));
memset(p, 0, sizeof(p));
printf("请输入矩阵链:\n");
for(int i = 0; i <= number; i++) scanf("%d", &p[i]);
MATRIX_CHAIN_ORDER(p, number);
PRINT_OPTIMAL_PARENS(s, 1, number);
printf("\n");
return 0;
}
矩阵连乘问题
1、实验结果
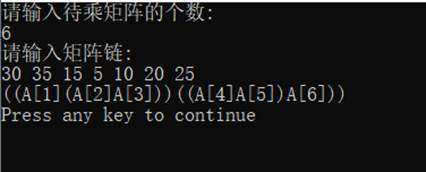
2、算法复杂度分析
时间复杂度:O(nnn)
(二)、投资问题
1、算法分析:
(1)只考虑第一个项目,即将所有的资金都投资给该项目,那么此时可以获取的利益可以计算出来;
(2)将第二个项目加进去,即投资的资金可以同时分配给两个项目,那么此时可以获取的利益可以计算出来;
(3)将第三个项目加进去,即投资的资金可以同时分配给三个项目,同样可以用上述方法得到此时能获取的利益。
后面以此类推。
2、代码实现:
#include<stdio.h>
#include<conio.h>
void main()
{
void jie(int,int,int d[][6]);
void Invest(int m,int n,int f[][6],int g[][6],int d[][6]);
int m=5,n=4,f[5][6],d[5][6];
int g[5][6]={{0},{0,11,12,13,14,15},
{0,0,5,10,15,20},{0,2,10,30,32,40},{0,20,21,22,23,24}};
Invest(m,n,f,g,d);
printf("可获得的最大收益为:%d\n",f[4][5]);
jie(m,n,d);
}
void Invest(int m,int n,int f[][6],int g[][6],int d[][6])
{
int i,j,k,s;
for(j=0;j<=m;j++)
{
f[1][j]=g[1][j];d[1][j]=j;}
for(i=2;i<=n;i++)
for(j=0;j<=m;j++)
{ f[i][j]=0;
for(k=0;k<=j;k++)
{
s=f[i-1][j-k]+g[i][k];
if(s>f[i][j])
{
f[i][j]=s; d[i][j]=k;
}
}
}
}
void jie(int m,int n,int d[][6])
{
int s=m; int k[5];
int i;
k[n]=d[n][m];
for(i=n-1;i>0;i--)
{
s = s-k[i+1];
k[i] = d[i][s];
}
for(i=1;i<=4;i++)
printf("%5d",k[i]);
printf("\n");
getch();
}
投资问题
1、实验结果
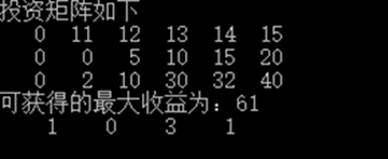
2、算法复杂度分析
时间复杂度: O(mnn)
(三)、完全背包问题
1、算法分析:
a) 把背包问题抽象化(X1,X2,…,Xn,其中Xi取0或1,表示第i个物品选或不选),Vi表示第i个物品的价值,Wi表示第i个物品的体积(重量);
b)建立模型,即求max(V1X1+V2X2+…+VnXn);
c)约束条件,W1X1+W2X2+…+WnXn<capacity;
d)定义V(i,j):当前背包容量j,前i个物品最佳组合对应的价值;
e)最优性原理是动态规划的基础,最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略”。
2、代码实现:
import numpy as np
# range(10)等于[0,1,2,3,4,5,6,7,8,9]
# range(1,10)等于[1,2,3,4,5,6,7,8,9]
# range(1,10,2)等于[1,3,5,7,9]
def main(number, bag_weight, weightList, valueList):
fk = [[0 for j in range(bag_weight + 1)] for i in range(number + 1)]
# 构造一个list(有number+1个元素,从0到number),其中每个元素也是一个list
# 并用0初始化,fk用来存放物品i取出的件数
valueExcel = [[0 for j in range(bag_weight + 1)] for i in range(number + 1)]
# valueExcel用来存放前i个物品中选出重量不超过j的物品总价值
for i in range(1, number + 1):
for j in range(1, bag_weight + 1):
for k in range((j // weightList[i-1])+1):
# 因为是list,第i个物品下标为i-1
if valueExcel[i][j] < (valueExcel[i - 1][j - k * weightList[i-1]] + k * valueList[i-1]):
valueExcel[i][j] = (valueExcel[i - 1][j - k * weightList[i-1]] + k * valueList[i-1])
fk[i][j] = k
# 遍历第i个物品的所有可能取值件数
print(np.array(valueExcel).reshape(number+1,-1))
# 改变输出形式
print(np.array(fk).reshape(number + 1, -1))
if __name__=="__main__":
print("请输入共有多少物品:", end=" ")
number = int(input())
print("请输入每个物品的价值:", end=" ")
valueList = list(map(int, input().split()))
# a = "1 2 3 4"
# print(list(map(int, a.split())))
# [1, 2, 3, 4]
# a.split()
# 表示把a字符串按照逗号切分成多个字符串存在一个列表中
# map(int, a.split())
# 表示把切分出的列表的每个值, 用int函数把它们转成int型, 并返回迭代器
# list(map(int, a.split()))
# 表示用list函数把map函数返回的迭代器遍历展开成一个列表
print("请输入每个物品的重量:", end=" ")
weightList = list(map(int, input().split()))
print("请输入背包重量", end=" ")
bag_weight = int(input())
main(number, bag_weight, weightList, valueList)
完全背包问题
1、实验结果

2、算法复杂度分析
时间复杂度:0(n^3)
(四)、旅行商问题
1、算法分析:
假定从城市1出发,经过了一些地方,并到达了城市j。毋庸置疑,我们需要记录的信息有当前的城市j。同时我们还需要记录已经走过的城市的集合。同理,使用S记录未走过的城市的集合也可以的,且运算方便。
于是可以得出状态转移方程 go(S,init)=min{go(S−i,i)+dp[i][init]} ∀s∈S ,go(s,init)表示从init点开始,要经过s集合中的所有点的距离。因为是NP问题,所以时间复杂度通常比较大。使用dis[s][init]来表示来回,初始化为-1,如果已经计算过init—>S(递归形式),则直接返回即可。
2、代码实现:
package algorithm;
public class TravelingSalesman
public static void main(String[] args) {
int cityCount = 4;
int[][] roadInfo = new int[][]{
{0, 1, 62},{1, 0, 65},{1, 3, 64},
{3, 1, 35},{3, 2, 16},{2, 3, 25},
{0, 2, 42},{2, 0, 45},{1, 2, 29},
{2, 1, 45} };
int roadmap[][] = new int[cityCount][cityCount]; //转成邻接矩阵方便取数
int dp[][] = new int[cityCount][1 << (cityCount - 1)];
//String path[][] = new String[cityCount][1 << (cityCount - 1)];
for (int i = 0; i < cityCount; i++) {
for (int j = 0; j < cityCount; j++) {
roadmap[i][j] = 0x7ffff; //用0x7ffff表示无穷大
}
}
for (int i = 0; i < roadInfo.length; i++) { //邻接矩阵
roadmap[roadInfo[i][0]][roadInfo[i][1]] = roadInfo[i][2];
}
for (int i = 0; i < cityCount; i++) { //先求dp表第一列
dp[i][0] = roadmap[i][0]; //求出了每个城市回到起点的距离了。
//记录初始路径。
}
for (int j = 1; j < 1 << (cityCount - 1); j++) { //再求其他列
for (int i = 0; i < cityCount; i++) { //从i出发,要去包含j = {010101}的 城市
dp[i][j] = 0x7ffff;
if (((j >> (i - 1)) & 1) == 1) { //如果已经到过j了,就continue
continue;
}
for (int k = 1; k < cityCount; k++) { //看能不能先到k城市
if (((j >> (k - 1)) & 1) == 0) {
continue; //不能先到k城市,continue;
}
if (dp[i][j] > roadmap[i][k] + dp[k][j ^ (1 << (k - 1))]) {
dp[i][j] = roadmap[i][k] + dp[k][j ^ (1 << (k - 1))];
//path[i][j] = i + path[k][j ^ (1 << (k - 1))]; //找到更短路径,覆盖之前结果。
}
}
}
}
System.out.println(dp[0][(1 << (cityCount - 1)) - 1]);
//System.out.println(path[0][(1 << (cityCount - 1)) - 1]);
System.out.println(" 动态规划表如下表所示");
System.out.printf("%10d", 0);
for (int j = 0; j < 1 << (cityCount - 1); j++) {
System.out.printf("%10d", j);
}
System.out.println();
for (int i = 0; i < cityCount; i++) {
System.out.printf("%10d", i);
for (int j = 0; j < 1 << (cityCount - 1); j++) {
if (dp[i][j] == 0x7ffff) dp[i][j] = -1;
System.out.printf("%10d", dp[i][j]);
}
System.out.println();
}
}
}
旅行商问题
1、实验结果
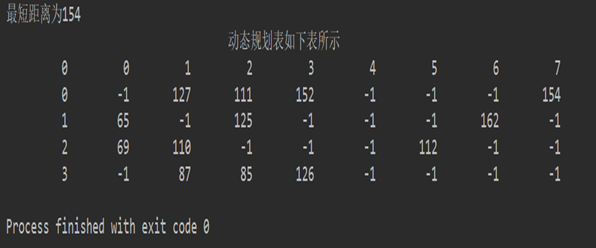 2、算法复杂度分析
2、算法复杂度分析
时间复杂度: n*2^(n-1)。
(五)、数字三角形
1、算法分析:
设 d( i , j )表示数字三角形中的第 i 行第 j 个点。 max[i][j]表示 第 i 行 第 j 个数字到低端的最佳路径之和,则原问题的解即为 max[1][1] 的值。从d( i,j )这个点向下走,显然只能走 d( i+1,j ) 和 d( i+1 ,j+1 ) 这两个点了。而 max[i][j] 的最优值= d( i,j) 的值 + max{ max[i+1][j] ,max[i+1][j+1] }。所以,我们可以至底向上来计算。先计算最后一层的点的,然后倒二层的,一直算到第一层。
2、代码实现:
#include <stdlib.h>
#include<stdio.h>
int main()
{
int n, a[101][101], d[101][101], i, j;
scanf("%d", &n);
for (i = 1; i <= n; i++)
for (j = 1; j <= i; j++)
scanf("%d", &d[i][j]);
for (j = 1; j <= n; j++)
a[n][j] = d[n][j];//从最后一行开始;
for (i = n - 1; i >= 1; i--)
for (j = 1; j <= i; j++)
{
if (a[i + 1][j + 1]>a[i + 1][j]) a[i][j] = d[i][j] + a[i + 1][j + 1];
else
a[i][j] = d[i][j] + a[i + 1][j];
}
printf("%d\n", a[1][1]);
system("pause");
return 0;
}
数字三角形
1、实验结果

2、算法复杂度分析
时间复杂度:0(n^2)
五、实验小结(包括问题和解决方法、心得体会等)
通过实现动态规划的题目,对动态规划有了更深的了解。动态规划算法是由单阶段的决策最优逐步转化为多阶段的决策最优,最后构造一个最优解。此次实验的Python代码部分由小组成员提供,每个人感兴趣的语言不一样,但是我们要做到能理解读懂,互相学习,相互提高。