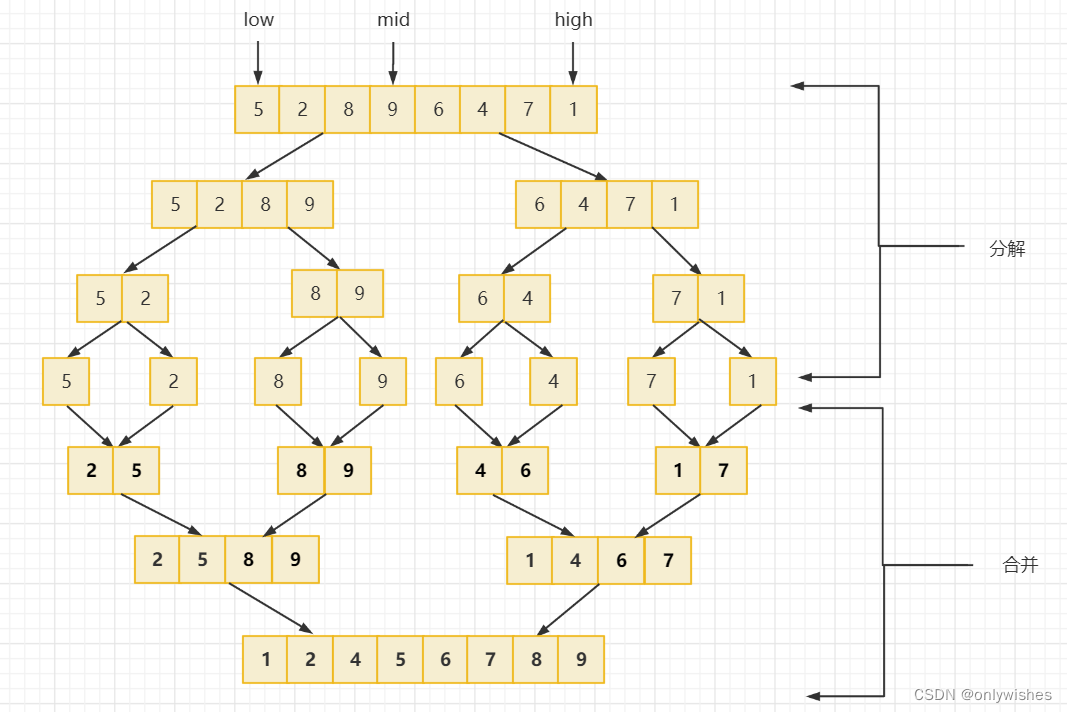
算法思想:
设初始序列含有n个记录,则可看成n个有序的子序列,每个子序列长度为1
两两合并,得到(n//2) 个长度为2(n为奇数时,最后一个序列的长度为1)的有序子序列
再两两合并,……如此重复,直至得到一个长度为n的有序序列为止
如图:以最后一次合并为例,序列2、5、8、9 和 序列1、4、6、7进行比较
- 2 > 1,将 1 加入新列表 ltmp 中第一个位置,两序列都不为空继续比较
- 2 < 4,将 2 顺序加入新列表ltmp 中 , 两序列都不为空继续比较
- 5 > 4,将 4 顺序加入新列表ltmp 中 , 两序列都不为空继续比较
- 5 < 6,将 5 顺序加入新列表ltmp 中 , 两序列都不为空继续比较
- 8 > 6,将 6 顺序加入新列表ltmp 中 , 两序列都不为空继续比较
- 8 > 7,将 7 顺序加入新列表ltmp 中 , 右边序列为空停止比较,将左边剩余序列全部加入列表ltmp中。本次归并结束。
- 将新列表ltmp 赋值给原列表相应位置元素。
当剩下两个序列且分别有序时,只要一次合并就可以使整个序列有序。
可以总结出二路归并基本操作是将待排序列中相邻的两个有序子序列合并成一个有序序列。
归并排序算法分析:
归并排序每一层都是n个数不变,每一层的复杂度为O(n),整个归并排序需进行m(m=log2n)趟2路归并,所以归并排序总的时间复杂度为O(nlog2n)。在实现归并排序时,需要和待排记录等数量的辅助空间,空间复杂度为O(n)。
实现思路:
先将序列分解为单个元素,即相邻元素都为有序序列。将相邻有序序列递归合并到新列表,可以分为下面三个步骤:
(1)首先递归分解序列直到出现单个元素(即相邻序列有序)
(2)对左部分序列和右部分序列进行归并
(3)将归并得到的新序列保存到原序列中对应位置
实现代码:
def merge(ls, low, mid, high):
"""
:param ls: 待排序列表
:param low: 最左下标
:param mid: 中间下标
:param high: 最右下标
:return: 返回一次归并后结果
"""
i = low
j = mid + 1
ltmp = [] # 新开列表,暂存归并结果
while i <= mid and j <= high: # 只要左右两边都有数,就能分
if ls[i] < ls[j]:
ltmp.append(ls[i]) # 左边与右边逐个对比将小的数加入ltmp新列表
i += 1
else:
ltmp.append(ls[j])
j += 1
# while执行完,必定有一部分没数了,序列为空
while i <= mid: # 若左边有数则逐个加入列表
ltmp.append(ls[i])
i += 1
while j <= high: # 若右边有数则逐个加入列表
ltmp.append(ls[j])
j += 1
ls[low:high + 1] = ltmp # 将一次归并后的列表赋值给原列表
def mergeSort(ls, low, high):
if low < high: # 至少两个元素,进行递归
mid = (low + high) // 2
mergeSort(ls, low, mid) # 对左部分递归
mergeSort(ls, mid + 1, high) # 对右部分递归
merge(ls, low, mid, high) # 对每个部分进行归并,整体有序
ls = [5, 2, 8, 9, 6, 4, 7, 1]
mergeSort(ls, 0, len(ls) - 1)
print(ls) # [1, 2, 4, 5, 6, 7, 8, 9]排序过程如图所示: