目录
今日知识点:
把状态压缩成j,dp每行i的布置状态,从i-1和i-2行进行不断转移
把状态压缩成j,dp每行i的布置状态,从i-1行进行状态匹配,然后枚举国王数转移
POJ1185:炮兵阵地
思路:
题目:互不侵犯
思路:
POJ1185:炮兵阵地
在N*M(N<100,M<10)的地图上布置炮兵,H格子为山地不能布置,P格子为平原可以布置。炮兵的攻击范围是沿横向左右各两格,沿纵向上下个两格子
炮兵之间不能误伤。问在整个地图中最多能拜访多少个炮兵?
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
思路:
还是那么句话,每个格子都有2种状态,如果搜索就要把所有结果都跑出来,所以只能使用状压dp 。
而且方程的转移和上一行的状态有关,但是状态又太多了,故要状态压缩。
首先要对行进行状态压缩(对列的话太大了,枚举2^100还不如不压缩呢),我们每次确定行的状态都需要考虑:
1.横向方案 2.横向方案是否和地图匹配 3.是否和i-1行i-2行冲突
设置dp[i][j][k]表示第i行为第j状态,第i-1行为第k状态时 对应的前i行放置的最大炮兵数。
转移方程:dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][t]+num[j]);(num是对应状态的炮兵个数)
(j是第i行的方案,k是第i-1行的方案,t是i-2行的方案)
存每行的可能状态:左右相邻1个间隔和2个间隔都不能炮兵(就是可能的横向方案)
存图:(1,1)开始存。0表示平原,1表示山地,那么在放置的时候不能出现同1(在山地放炮兵),所以x&y=0是合法的(保证合法的是0就行了)
是否冲突:第i行和第i-1行,第i-2行 不能出现有一列同1(两行都放炮兵),所以x&y=0是合法的
【注意】:外面每行i循环一次,其次里面是第i行的每个状态j循环一次(找到合适的j),然后是第i-1行的每个状态k循环一次(供第i行找到合适的k),
接着是第i-2行的每个状态t循环一次(供第i-1行找到合适的t)
#include <bits/stdc++.h>
using namespace std;
int n,m,top;
char mp[110][20];
int num[70];//num存放状态对应的炮兵个数
int ok[70],cur[70];//ok表示横向可能的方案,cur是我们存的地图行
int dp[110][70][70];
bool check(int x){
if(x&(x<<1))return 0;//相邻1间隔是否合法
if(x&(x<<2))return 0;//相邻2间隔是否合法
return 1;
}
void init(){//统计所有的可能合法状态,最多60种
top=0;
for(int i=0;i<(1<<m);i++){//不能取等,不能取等!!!
if(check(i))ok[top++]=i;
}
}
int count(int x){//统计x二进制中1的个数
int cnt=0;
while(x){
if(x&1)cnt++;
x=x>>1;
}
// while(x){//这个更快
// cnt++;
// x&=(x-1);
// }
return cnt;
}
int solve(){
int ans=0;
memset(dp,-1,sizeof(dp));
for(int j=0;j<top;j++){//初始化第一行的状态
num[j]=count(ok[j]);//记录每个正确状态的炮兵个数
if(!(ok[j]&cur[1])){//和地图匹配
dp[1][j][0]=num[j];//第一行状态为j,上一行状态为0(知道为啥从(1,1)开始初始化了把)
ans=max(ans,dp[1][j][0]);
}
}
for(int i=2;i<=n;i++){//处理每一行
for(int j=0;j<top;j++){//遍历第i行的可能方案
if(ok[j]&cur[i])continue;//是否和地图匹配
for(int k=0;k<top;k++){//遍历第i-1行的可能方案
if(ok[j]&ok[k])continue;//此行和上一行是否匹配(不用再判断和地图是否匹配,不匹配dp是-1,不影响的)
for(int t=0;t<top;t++){//遍历上二行可能方案
if(ok[j]&ok[t])continue;//此行和上二行是否匹配
dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][t]+num[j]);
}
if(i==n)ans=max(ans,dp[i][j][k]);//不要放在外面套3个for取max
}
}
}
return ans;
}
int main(){
while(cin>>n>>m){
init();
for(int i=1;i<=n;i++){
scanf("%s",mp[i]+1);//加1是为了从1下标开始存
}
for(int i=1;i<=n;i++){
cur[i]=0;
for(int j=1;j<=m;j++){
if(mp[i][j]=='H')//同样的,不能放的地方存1
cur[i]+=(1<<(m-j));
}
}
cout<<solve();
}
}
题目:互不侵犯
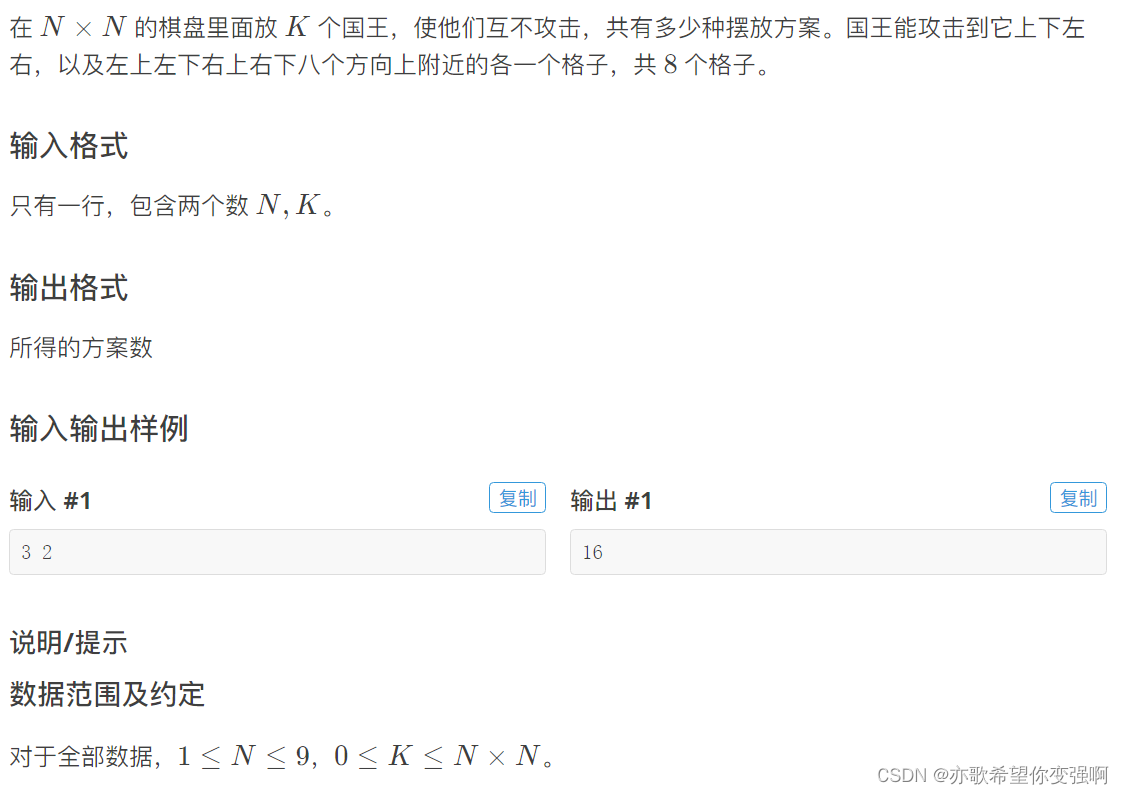
思路:
可以看到和炮兵阵地题非常像,跑不了是状压dp。
还是那句话,每个方格都有两种状态,搜索的话必然是要全部搜索一下,放弃吧(况且,不谈超时,你真的把本道题的dfs其实也够呛的)。
设置dp[i][j][k]表示第i行为j状态时已经放了k个国王对应的方案数。
转移方程:dp[i][j][k]=dp[i-1][i-1行所有的合法状态][k-对应状态的国王数];
然后就是对状态的处理:
行内状态:我们要保证相与出0合法,非0不合法。那么对s行,
有:(((s<<1)&s==0)&&((s>>1)&s)==0)算合法,
等价于这个写法:(((s<<1)|(s>>1))&s)==0。 千万别少写红色括号!!!
行间状态:((s2&s1==0)&&((s2>>1)&s1==0)&&((s2<<1)&s1)==0)才算合法,
等价于:(((s2|(s2>>1)|(s2<<1))&s1)==0。
循环方式:首先是每行,然后选择该行状态,然后是上行状态,判断两行状态是否匹配,如果匹配就枚举国王数,最后转移方程!
#include <bits/stdc++.h>
using namespace std;
int num,n,k;//ok存正确的行状态,cnt存状态对应的国王数
long long dp[10][100][2000],cnt[2000],ok[2000];
int main(){
cin>>n>>k;
for(int s=0;s<(1<<n);s++){//遍历出所有的正确状态i
int tot=0,tmp=s;
while(tmp){
if(tmp&1)tot++;tmp>>=1;
}
cnt[s]=tot;//存每个状态的国王数
if((((s<<1)|(s>>1))&s)==0) ok[++num]=s;
}
dp[0][0][0]=1;
for(int i=1;i<=n;i++){//从第一行开始转移
for(int ss1=1;ss1<=num;ss1++){
int s1=ok[ss1];//选择第一行的状态
for(int ss2=1;ss2<=num;ss2++){
int s2=ok[ss2];//选择上一行的状态
if(((s2|(s2<<1)|(s2>>1))&s1)==0){//如果这两行状态合法
for(int j=0;j<=k;j++){//对国王数进行枚举转移
if(j-cnt[s1]>=0)
dp[i][j][s1]+=dp[i-1][j-cnt[s1]][s2];
}
}
}
}
}
long long ans=0;
for(int i=1;i<=num;i++)
ans+=dp[n][k][ok[i]];
cout<<ans;
}