Leslie模型是一种用于离散时间的生物种群增长模型,经常用于描述年龄结构对种群增长的影响。在1945年,人口生态学家Patrick H. Leslie(莱斯利)为了研究具有离散年龄结构的种群,特别是对于有不同年龄阶段的生物,如昆虫、鱼类、鸟类等,提出了Leslie模型。
Leslie模型的基本思想是,将种群划分为不同年龄阶段(类别),然后根据不同年龄阶段的生存率和繁殖率来预测未来的种群变化。模型中的年龄结构是离散的,通常划分为几个年龄组。这个模型对于研究种群的年龄结构和生命周期变化非常有用。
模型建立
- 在某动物种群中,仅考查雌性动物的年龄和数量;
- 设雌性动物的最大生存年龄为
(单位:年);
- 把
等分为
个年龄组,每一年龄组的长度为
;
个年龄组分别为(从第1组到第
组)
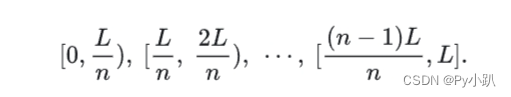
- 设第
个年龄组的生育率为
,存活率为
(
=1,2,⋯,
),
,
均为常数,且
- 设至少有一个
>0 (1≤
≤
);
- 即至少有一个年龄组的雌性动物具有生育能力.
- 由统计资料可获得基年(
=0)该种群在各年龄组的雌性动物数量.
- 记
(
=1,2,⋯,
)为
=0时第
年龄组雌性动物的数量.
- 初始时刻各年龄组种群数量分布向量
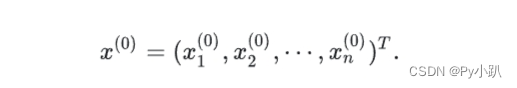
- 若以年龄组的间隔
作为时间单位,记

- 在
时各年龄组种群数量分布向量
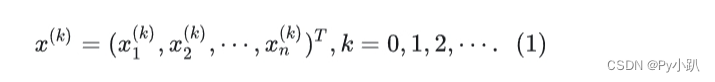
- 随着时间的变化,由于出生、死亡以及年龄的增长,该种群中每一个年龄组的雌性动物数量都将发生变化.
- 在
时刻,种群中第1个年龄组的雌性动物数量应等于在
和
之间出生的所有雌性幼体的总和,即

- 同时,在
时刻,第
个年龄组(
=1,2,⋯,
-1)中雌性动物的数量应等于在
时刻第
个年龄组中雌性动物数量
乘存活率
,即
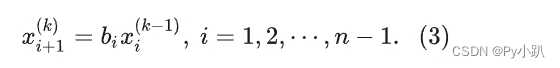
- 由式(2-3)可得在
和
时刻各年龄组中雌性动物数量间的关系:
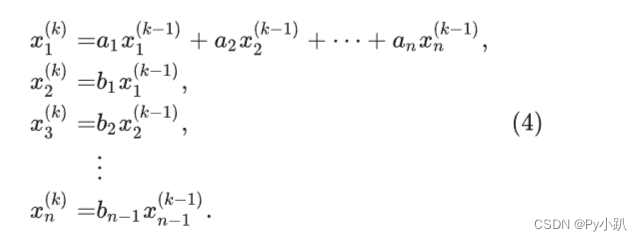
- 记矩阵

- 式(3)可写成
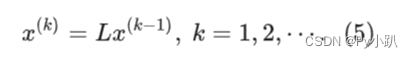
- 称
为莱斯利矩阵(Leslie).
- 由式(5),可得
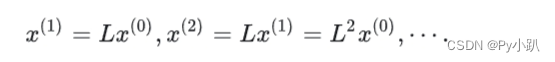
- 一般地
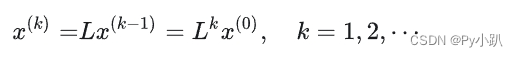
- 若已知初始时各年龄组种群数量分布向量
,则可推算任一时刻
该种群数量分布向量.
以上是相关理论介绍,下面举例说明
示例
- 某种动物雌性的最大生存年龄为15年,
- 以5年为一间隔,把这一动物种群分为3个年龄组[0,5),[5,10),[10,15],
- 利用统计统计资料,已知生育率和存活率分别为:
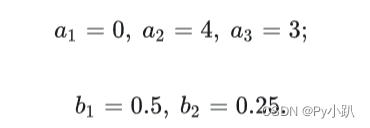
- 在初始时刻
时,3个年龄组的雌性动物个数分别为500,1000,500
- 初始种群数量分布向量和莱斯利矩阵为:

- 于是

- 为了分析当
时,该动物种群数量分布向量的特点,先求出矩阵
的特征值与特征向量.
- 计算
的特征多项式
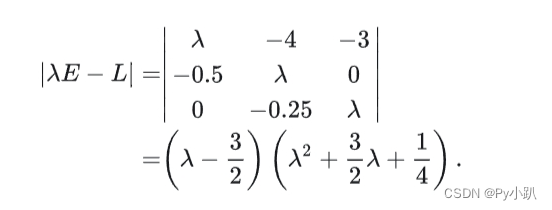
- 由此可得
的特征值
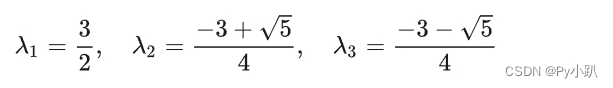
是矩阵
的唯一正特征值,且
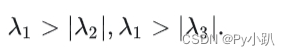
有3个互异特征值,因此矩阵
可相似对角化.
- 设矩阵
属于特征值
(
=1,2,3)的特征向量为
.
- 计算
属于特征值
=
的特征向量为
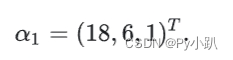
- 记矩阵
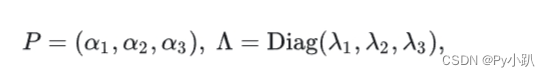
- 则
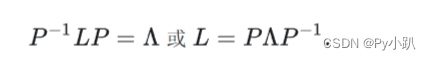
- 因此
=
.
- 矩阵对角化可参考矩阵对角化(Diagonalizing a Matrix)-CSDN博客
- 于是有:

- 即
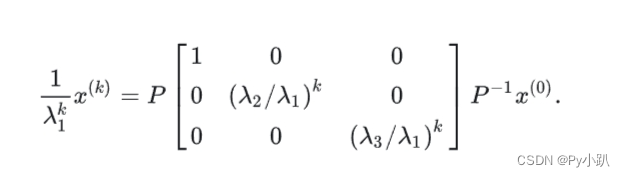
- 因为
,
,所以:
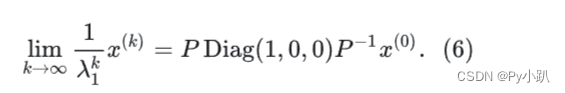
- 记列向量
的第一个元素为
(常数),则式(6)可化为
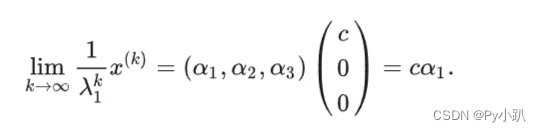
- 当
充分大时,近似地成立
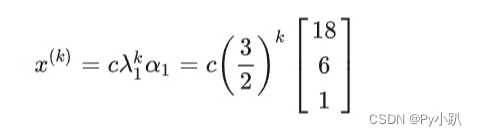
其中=
.
- 当时间充分长,这种动物中雌性的年龄分布将趋于稳定,即3个年龄组的数量比为18:6:1.
- 可近似得到在
时刻种群中雌性动物的总量,从而对整个种群的总量进行估计.
- 莱斯利模型在分析动物种群的年龄分布和总量增长方面有广泛应用,也可应用于人口增长的年龄分布问题.
【提示:以上涉及高数内容对很多伙伴包括我很困难,大家可以结合后面的编程内容,交互学习,能看懂算出结果比推导公式明白原理更重要】
Python编程计算代码如下:
import numpy as np # 导入NumPy库,并简化为np
import sympy as sp # 导入SymPy库,并简化为sp
# 定义初始向量X0
X0 = np.array([500, 1000, 500])
# 定义矩阵L
L = np.array([[0, 4, 3], [0.5, 0, 0], [0, 0.25, 0]])
# 矩阵乘法计算X1和X2
X1 = L @ X0; X2 = L @ X1 # @表示矩阵乘法
X3 = L @ X2
# 定义符号矩阵Ls
Ls = sp.Matrix([[0, 4, 3], [sp.Rational(1,2), 0, 0],
[0, sp.Rational(1,4), 0]]) # 使用Rational来确保精确计算
# 定义符号变量lamda
sp.var('lamda')
# 计算特征多项式
p = Ls.charpoly(lamda)
# 计算特征根
w1 = sp.roots(p)
# 直接计算特征值
w2 = Ls.eigenvals()
# 直接计算特征向量
v = Ls.eigenvects()
# 打印特征值和特征向量
print("特征值为:", w2)
print("特征向量为:\n", v)
# 相似对角化
P, D = Ls.diagonalize()
# 求逆矩阵
Pinv = P.inv()
# 简化逆矩阵
Pinv = sp.simplify(Pinv)
# 将逆矩阵应用于初始向量X0
cc = Pinv @ X0
# 打印变换矩阵P和变换后的系数c
print('P=\n', P)
print('c=', cc[0])结果输出:
特征值为: {3/2: 1, -3/4 - sqrt(5)/4: 1, -3/4 + sqrt(5)/4: 1}
特征向量为:
[(3/2, 1, [Matrix([
[18],
[ 6],
[ 1]])]), (-3/4 - sqrt(5)/4, 1, [Matrix([
[3*sqrt(5) + 7],
[ -3 - sqrt(5)],
[ 1]])]), (-3/4 + sqrt(5)/4, 1, [Matrix([
[7 - 3*sqrt(5)],
[ -3 + sqrt(5)],
[ 1]])])]
P=
Matrix([[18, 3*sqrt(5) + 7, 7 - 3*sqrt(5)], [6, -3 - sqrt(5), -3 + sqrt(5)], [1, 1, 1]])
c= 2250/19
- 如要计算第k=2个时期的种群数量,代码如下:
# 导入numpy库,用于数组操作
import numpy as np
# 导入sympy库,用于符号计算
import sympy as sp
# 定义一个初始种群向量X0,包含三个年龄段的种群数量
X0 = np.array([500, 1000, 500])
# 定义Leslie矩阵L,描述了不同年龄段种群的转化关系
L = np.array([[0, 4, 3], [0.5, 0, 0], [0, 0.25, 0]])
# 计算第一年的种群向量X1,即L乘以初始种群向量X0
X1 = L @ X0
# 计算第二年的种群向量X2,即L乘以第一年的种群向量X1
X2 = L @ X1
# 计算第三年的种群向量X3,即L乘以第二年的种群向量X2
X3 = L @ X2
# 定义符号矩阵Ls,这里使用了Rational来确保计算中的分数是精确的
Ls = sp.Matrix([[0, 4, 3], [sp.Rational(1, 2), 0, 0], [0, sp.Rational(1, 4), 0]])
# 定义符号变量lamda,用于特征多项式的计算
lamda = sp.var('lamda')
# 计算矩阵Ls的特征多项式
p = Ls.charpoly(lamda)
# 注释掉了计算特征值和特征向量的代码,因为在后面有重新计算
# w11 = Ls.eigenvals()
# w22 = Ls.eigenvects()
# 计算特征多项式的根,即特征值
w1 = sp.roots(p)
# 直接计算矩阵Ls的特征值
w2 = Ls.eigenvals()
# 直接计算矩阵Ls的特征向量
v = Ls.eigenvects()
# 注释掉了打印特征值和特征向量的代码
# print("特征值", w2)
# print(w1)
# print('特征向量', v)
# 对矩阵Ls进行相似对角化,得到变换矩阵P和对角矩阵D
P, D = Ls.diagonalize()
# 计算变换矩阵P的逆矩阵
Pinv = P.inv()
# 简化逆矩阵Pinv
Pinv = sp.simplify(Pinv)
# 将逆矩阵Pinv应用于初始种群向量X0,得到变换后的系数cc
cc = Pinv @ X0
# 注释掉了打印变换矩阵P和系数cc的代码
# print(P)
# print(cc[0])
# print(w1)
# print(v)
# 定义符号变量k,表示时期数,且k为正整数
k = sp.var('k', positive=True, integer=True)
# 计算第k个时期的种群数量,通过相似对角化后的形式进行计算
xk = P @ (D ** k) @ Pinv @ sp.Matrix(X0)
# 注释掉了打印第k个时期种群数量和特定元素的代码
# print(xk)
# print(xk[0])
# 简化第k个时期的种群数量表达式
s = sp.simplify(xk[0])
# 将k替换为2,并计算数值结果,即第二个时期的种群数量
print(s.subs(k, 2).n())结果输出【中间部分代码进行了注释,大家可以根据需要打开学习】:
1750.00000000000
参考文献
[1] 司守奎,孙兆亮. Python数学建模算法与应用. 北京:国防工业出版社,2022.
本文内容来源于《Python数学建模算法与应用》教材和网络,仅供参考学习,如内容、图片有任何版权问题,请联系处理,24小时内删除。