Python 八级
2024 年 03 月
1 单选题（每题 2 分，共 30 分）
第 1 题 下列代码中，用到的算法是什么算法，去掉存储的空间，算法本身用到的空间复杂度是多少（ ）

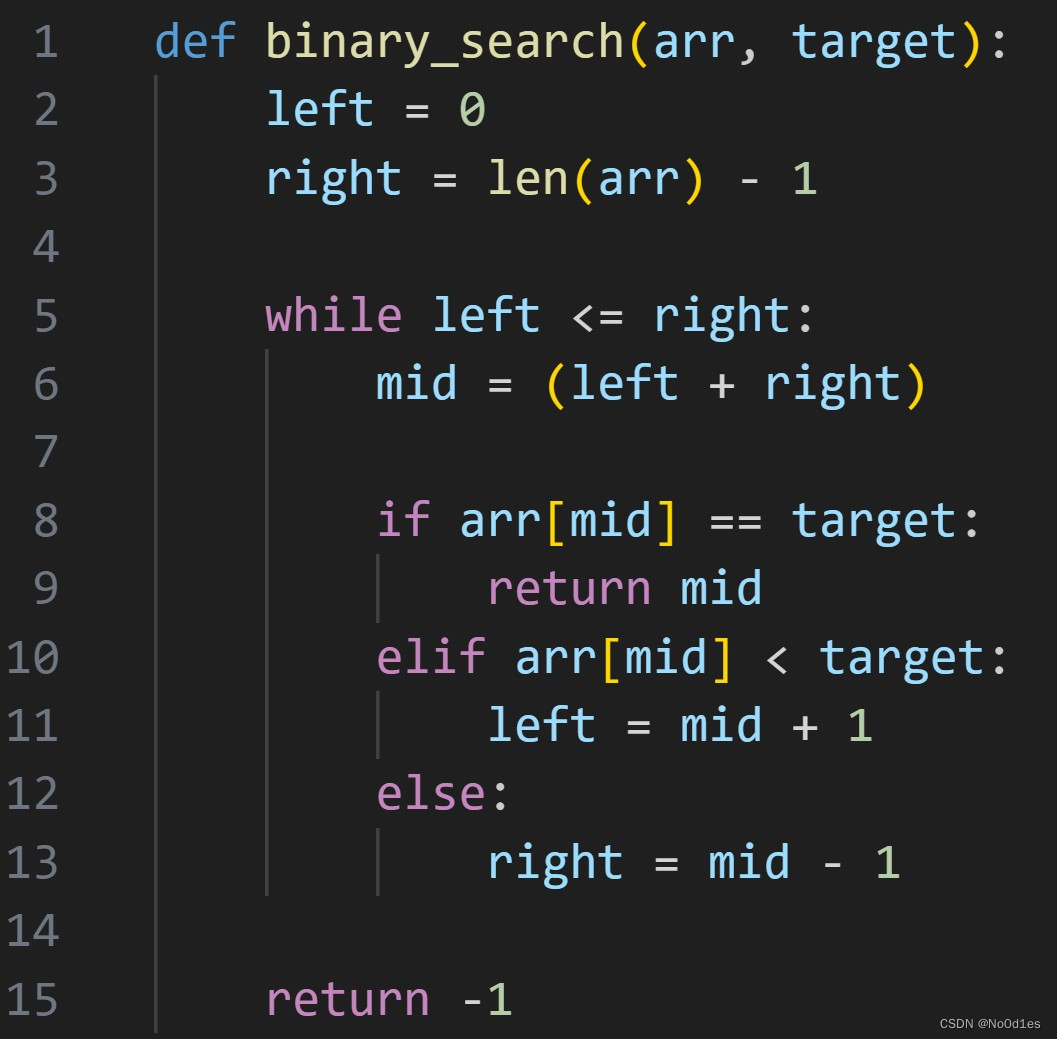
A. 二分法 ， O(log2N)
B. 二分法 ， O(N)
C. 折半查找 ， O(1)
D. 折半查找 ， O(Nlog2N)

第 2 题 无向图的临接矩阵存储方法中，下列描述正确的是（ ）。
A. 对角矩阵
B. 稀疏矩阵
C. 非对称矩阵
D. 对称矩阵

第 3 题 下列代码依次输入10,3,2后，结果是（ ）。

A. 23
B. 120
C. 16
D. 155

第 4 题 一个等边五边形，每个顶点上有一个蚂蚁，蚂蚁沿着五边形的边严格匀速行走，方向随机，请问，开始走以后，蚂蚁两两不相碰的概率是多少（ ）。
A. 1/16
B. 1/4
C. 1/32
D. 1/8

第 5 题 一根长度为1的小木棒，随机的折成三段，请问这三段能够组成一个三角形的概率是多少？（ ）。
A. 1/3
B. 1/4
C. 1/8
D. 1/2

第 6 题 有北京，雄安，天津三个城市，同样两个城市之间来回票价一样。请问火车售票部门需要准备几种车票，几
种票价（ ）。
A. 3,3
B. 6,6
C. 6,3
D. 3,6

第 7 题 对于如下图的无向图，在用Prim算法以节点F作为起点生成最小树的过程中，哪个选项不是产生最小树的中间状态？（ ）。

A.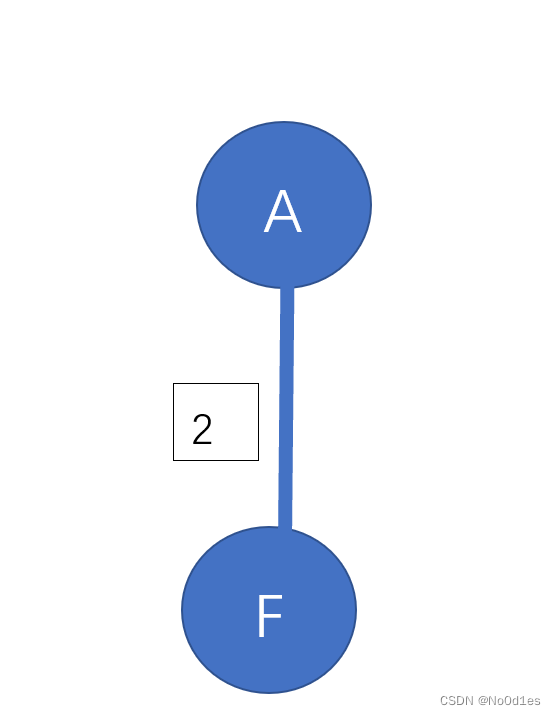
B.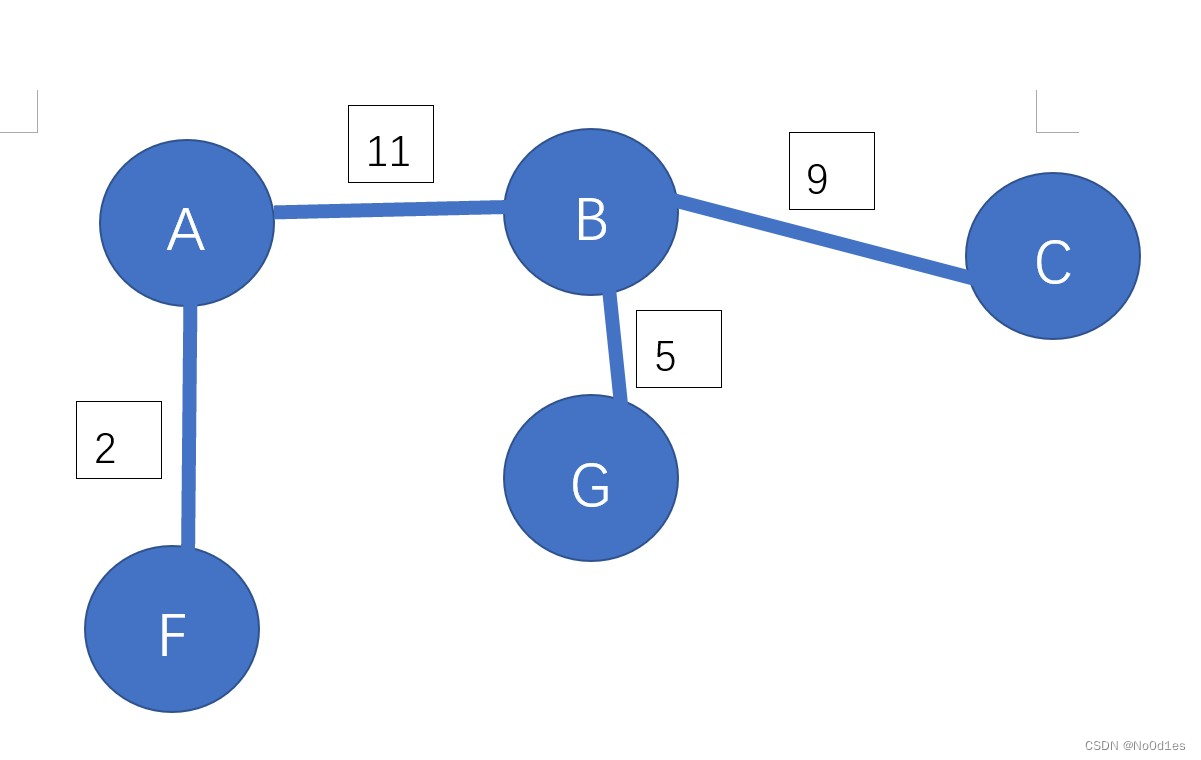
C.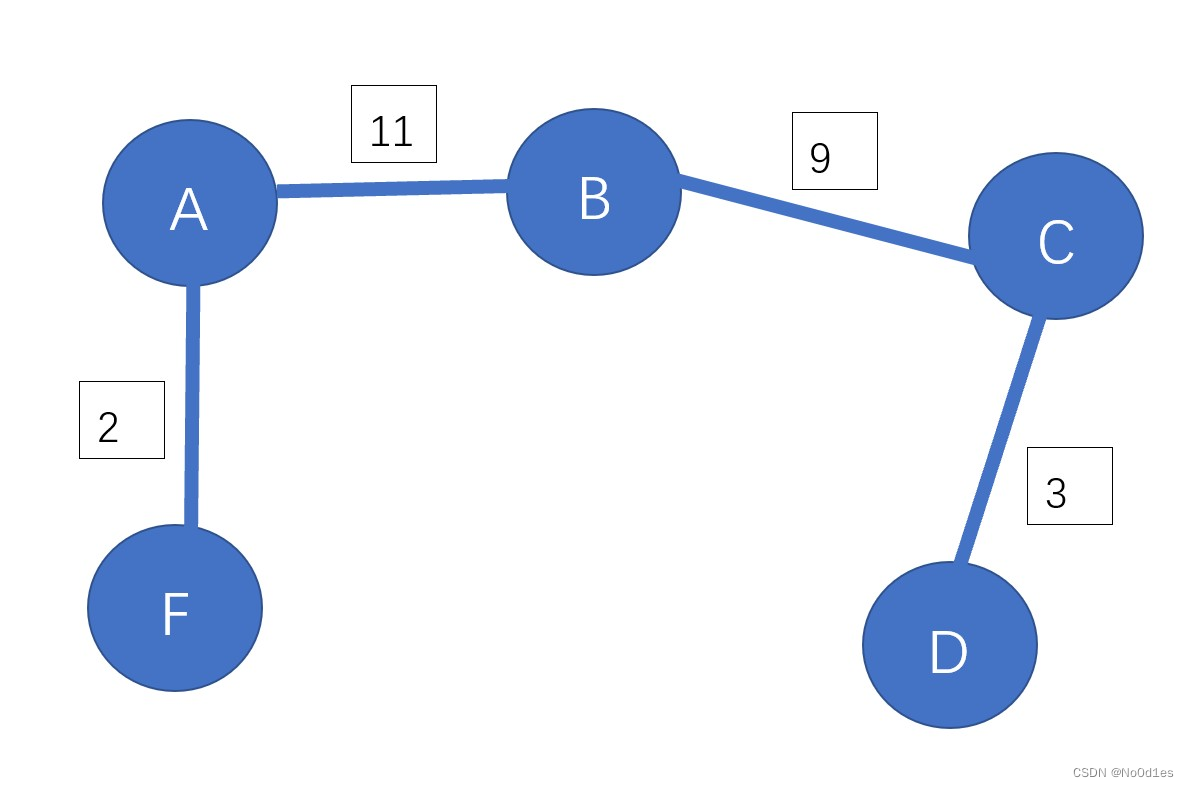
D.

第 8 题 对于一棵是完全二叉树的排序二叉树，其平均搜索的时间复杂度为（ ）。
A.
B.
C.
D.

第 9 题 关于快速幂，下列说法错误的是（ ）。
A. 使用了倍增思想
B. 每一步都把指数分成两半，而相应的底数做平方运算
C. 时间复杂度为
D. 可以用快速幂方法计算斐波那契数列的第 项

第 10 题 下面实现杨辉三角形的程序中，横线处填写正确的是（ ）。

A. z = triangles(x, y-1) + triangles(x, y)
B. z = triangles(x-1, y+1) + triangles(x-1, y-1)
C. z = triangles(x-1, y-1) + triangles(x, y)
D. z = triangles(x-1, y-1) + triangles(x-1, y)

第 11 题 设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的盒子，现将这5个球投入5个盒子要求每个盒子放一个球，并且恰好有两个球的号码与盒子号码相同，问有多少种不同的方法（ ）。
A. 20
B. 10
C. 12
D. 24

答案和更多内容请查看网站：【试卷中心 -- Python  其它】

网站链接 

青少年软件编程历年真题模拟题实时更新

================================================