三、 数据结构:
时间复杂度:
- 背复杂度对应的代码。
- Tips:时间复杂度估算看最内层循环,如若没有循环和递归则为O(1)。

空间复杂度:
- 需要单独空间存储数据时使用。
- 考点:非递归的空间复杂度。
- Tips:声明一个变量和有限个数的变量都是O(1)。

递归式:
时间/空间复杂度:
- 递归算法的时间/空间复杂度 = 递归的次数 × 每次递归的时间/空间复杂度
- 上述适用于每次递归时间复杂度不变的情况。
- 如果每次递归的时间复杂度随着n变化而变化,则要根据代码来观察。

主方法求递归式:(似懂非懂)

指数计算公式:

线性表:
- 考点:如果没有给出最好最坏平均时间复杂度的话,默认是平均时间复杂度。
顺序表:
- 插入、删除操作最好时间复杂度为O(1),平均和最坏时间复杂度都为O(n)。
- 查找最好、最坏、平均情况都为O(1)。
单链表:
- 查找、插入、删除操作最好时间复杂度为O(1),平均和最坏时间复杂度都为O(n)。
顺序存储:
- 通过元素在存储空间中的相对位置来表示数据元素之间的逻辑关系。
队列:
- 优先队列通常采用 堆 数据结构实现,向优先队列中插入一个元素的时间复杂度为O( lgn)。
数组:
一维数组:
- LOC:数组首地址、L:元素大小。
- 下标从0开始:a_i = LOC + i × L
- 下标从1开始:a_i = LOC + ( i - 1) × L
- Tips:理解记忆。
二维数组:a[i][j] -> i表示行,j表示列
- LOC:数组首地址、N:行数、M:列数、L:元素大小
- 按行优先存储并且下标从0开始:a_(i,j) = LOC + (i × M + j) × L
- 按行优先存储并且下标从1开始:a_(i,j) = LOC + [(i - 1) × M + (j-1)] × L
- 按列优先存储并且下标从0开始:a_(i,j) = LOC + (j × N + i) × L
- 按列优先存储并且下标从1开始:a_(i,j) = LOC + [(j - 1) × N + (i - 1)] × L
- Tips:理解记忆。
矩阵:
对称矩阵:
概念:
- 有一个n×n的矩阵,若矩阵中的任意一个元素都有A_(i,j) = A_(j,i),则该矩阵为对称矩阵。
考点:
- 一般考存储下三角和主对角线;按行优先存储;基于一维数组下标从1开始存储的公式。
对称矩阵按行存储下三角区和主对角线并且下标从1(A_1,1)开始的公式:
- 当(i≥j)时:A_(i,j) = i(i - 1) / 2 + j
- 当(i≤j)时:A_(i,j) = j(j - 1) / 2 + i
- ---- ----
- 对称矩阵按行存储下三角区和主对角线并且下标从0(A_0,0)开始:
- 当(i≥j)时:A_(i,j)=i(i+1)/2+j+1
- 当(i≤j)时:A_(i,j)=j(j+1)/2+i+1
三对角矩阵:
概念:
- 有一个n×n矩阵A称为三对角矩阵,其中第(i,j)个元素在j > i + 1和j < i - 1时为零。
考点:
- 按行优先存储。
三对角矩阵按按存储并且下标从1(A_1,1)开始的公式:背
- A_(i,j) = 2i + j - 2
- ---- ----
- 三对角矩阵按按存储并且下标从1(A_1,1)开始:A_(i,j) = 2i + j - 2
稀疏矩阵:
- 三元组顺序表和十字链表是对稀疏矩阵进行压缩存储的方式。背
上述三种矩阵图例:

二叉树:
- 完全二叉树、满二叉树概念。
- 性质3。

二叉树的存储结构:
- 顺序存储需要维护结点和左、右孩子的关系:结点编号为n,则左孩子为2n,右孩子为2n+1。
- 链式存储有二叉链表和三叉链表。
- 对于个结点n的二叉树,二叉链表的空指针为n+1,三叉链表的空指针为n+2。
二叉树的遍历:
- 先序遍历和后序遍历,不能构造中序遍历。
- 通过序列构造二叉树必须有中序序列。
平衡二叉树:
- 左右子树高度差不能大于1。
有序二叉树:
- 有序二叉树,就是左子树上的数值小于树根上的值,树根上的值小于右子树的值。左右子树也是一颗二叉排序树。
- 最坏的查找情况是单枝树(即高度h为n)要查找n次。
二叉排序树关键字排序:
- 第一位为根节点,第二位与根节点比较插入到树中,依次类推。
最优二叉树(哈夫曼树):
- 概念:它是一类带权路径长度最短的树。路径是从书中一个结点到另一个结点之间的通路,路径上的分支数目为路径长度。
- 哈夫曼树中权值越大的结点离根结点越近,权值越小的结点离根结点越远。
- 哈夫曼树只有度为0和度为2的结点,没有度为1的结点。
- n个权值构造的哈夫曼树具有2n-1个结点。
- 哈夫曼编码,基于贪心算法。
- 哈夫曼树中最小的两个结点互为兄弟结点。
构造最优二叉树:
- 方法:

- 规则:***
- 1. 从前往后找两个权重最小。2. 小左大右。3. 加入末尾。4. 权值相同从前往后。5. 用时再调。
压缩比计算:
- 概念:求等长编码到哈夫曼编码压缩了多少。
- 等长编码需要多少位。-> 公式:2^x >= 字符个数,x为需要多少位。
- 哈夫曼编码是变长编码,在哈夫曼树中,从根节点开始,给左右分支标记0,1。即一层节点占一位。
- 压缩比 =(等长编码长度 - 哈夫曼编码车长度) / 等长编码长度
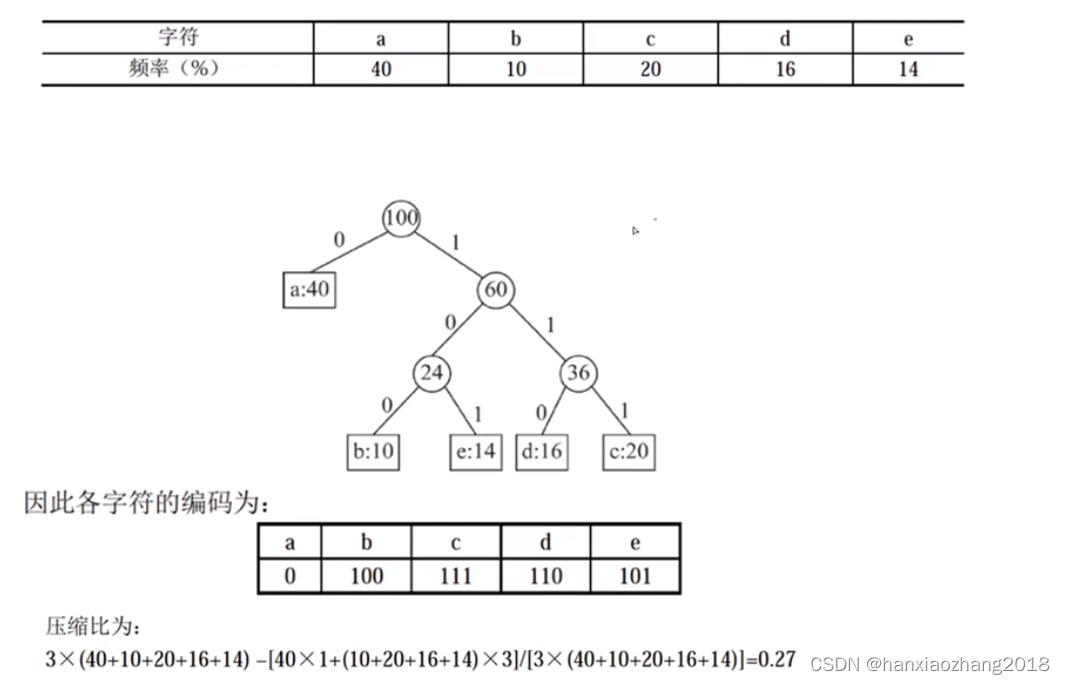
图:
有向图、无向图:
- 无向图:连接顶点的边是无向边
- 有向图:连接顶点的边是有向边(弧)
- ---- ----
- 有向图和无向图的所有顶点度数之和 2e。(e为边数)
- 有向图和无向图的边数 e = 顶点度数之和/2。
完全图:
- 概念:每对顶点之间都恰连有一条边的图。
- 无向完全图:(n*(n-1)) / 2 条边
- 有向完全图:n*(n-1) 条边
连通图:
- 连通图:无向图中任意两个顶点之间都有路径。最少有n-1条边,最多有(n*(n-1))/2条边。
- 强连通图:有向图中任意两个顶点之间都有路径。 最少有n条边,最多有n*(n-1)条边。
最小生成树:
最小生成树-普利姆(Prim)算法:
- 贪心算法。
- 思想:从任意一个顶点开始,沿着权重最小的边进行扩展。
- 时间复杂度:O[n2]

最小生成树-克鲁斯卡尔(Kruskal)算法:
- 贪心算法。
- 思想:每次选择权重最小的边来将两个顶点连接起来。
- 时间复杂度为O[elog e]。
----- ----- -----
- 若网较稠密,则Prim算法更好。
邻接矩阵:
- 概念:表示顶点之间相邻关系的矩阵。
- 查找所有顶点的邻居顶点的时间复杂度为O(n^2)。
邻接链表表示法:
- 邻接表更适合存储稀疏图(边数很少的图)
- 无向图采用邻接表存储有2e个表结点(e为边数)。
- 有向图采用邻接表存储有n+e个表结点(n为结点数,e为边数) 。
哈希表:
- 用线性探测法解决冲突容易产生聚集问题。
查找:
折半(二分)查找:
- 折半查找在查找成功时,关键字的比较次数最多为 log2(n) +1 。
- 折半查找的时间复杂度为O(log2n)。
- 要求元素顺序存储,元素有序排列。
- 考题:
- mid = (low+high)/2 取整, k > mid时, low = mid+1,k。并且注意细节
不能构成查找过程中关键字比较序列考题:
- 解题规律:比较序列可能是:大大大... ...大、小小小... ...小 、小大小大... ...小 大、大小大小... ...大小
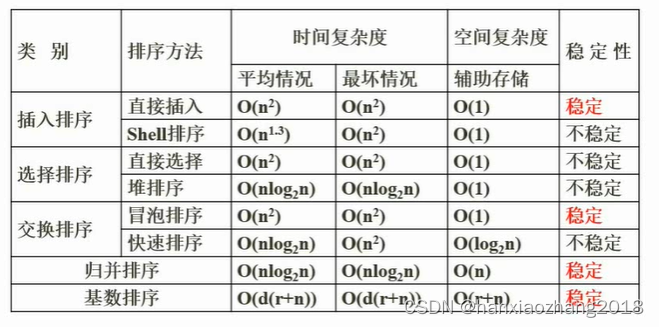
排序:
- 当数列基本有序时,采用插入排序比较合适,使用插入排序中希尔排序。背
- 一定范围内的整数排序时,使用基数排序。例如:需要排序的记录是0-9的整数。
- 快速排序:采用分治思想。最坏O(n^2),平均O(nlog2^n),一趟排序O(n)。基本有序时,快排具有最坏的情况。最佳的基准元素为中位数划分。
- 归并排序:采用分治思想。时间复杂度,最好最坏一致O(nlog2^n)。稳定。
- 堆排序:不稳定。空间复杂度O(1)。
堆:
使用数组构建大顶堆:
- 将数组转换成二叉树。
- 从最后一层的非叶子节点开始与叶子节点调整。一层一层的调整。调整过后导致已经调整的层大小顺序相反,则继续调整。