关系（三）利用python绘制相关矩阵图

相关矩阵图（Correlogram）简介

相关矩阵图既可以分析每对变量之间的相关性，也可以分析单变量的分布情况。相关性以散点图的形式可视化，对角线用直方图/密度图表示每个变量的分布。

快速绘制

1. 基于seaborn

   import seaborn as sns
   import matplotlib.pyplot as plt
   
   # 导入数据
   df = sns.load_dataset('iris')
   
   # 利用pairplot函数绘制相关矩阵图
   sns.pairplot(df)
   
   plt.show()
   

   

2. 基于matplotlib

   import matplotlib.pyplot as plt
   
   # 导入数据
   df = sns.load_dataset('iris')
   
   # 定义基本变量
   COLUMNS = ["sepal_length", "sepal_width", "petal_length", "petal_width"]
   COLORS = ["#386cb0", "#fdb462", "#7fc97f"]
   SPECIES = ["setosa", "versicolor", "virginica"]
   
   # 初始化布局4*4
   fig, axes = plt.subplots(4, 4, figsize = (12, 8), sharex="col", tight_layout=True)
   
   for i in range(len(COLUMNS)):
       for j in range(len(COLUMNS)):
           # 下三角添加散点图
           if i > j:
               for species, color in zip(SPECIES, COLORS):
                   data = df[df["species"] == species]
                   axes[i, j].scatter(COLUMNS[j], COLUMNS[i], color=color, alpha=0.5, data=data)
                   
           # 对角线添加直方图
           if i == j:
               for species, color in zip(SPECIES, COLORS):
                   data = df[df["species"] == species]
                   axes[i, j].hist(COLUMNS[j], bins=15, alpha=0.5, data=data)
           
           # 上三角剔除边框
           if i < j:
               axes[i, j].remove()
               
   plt.show()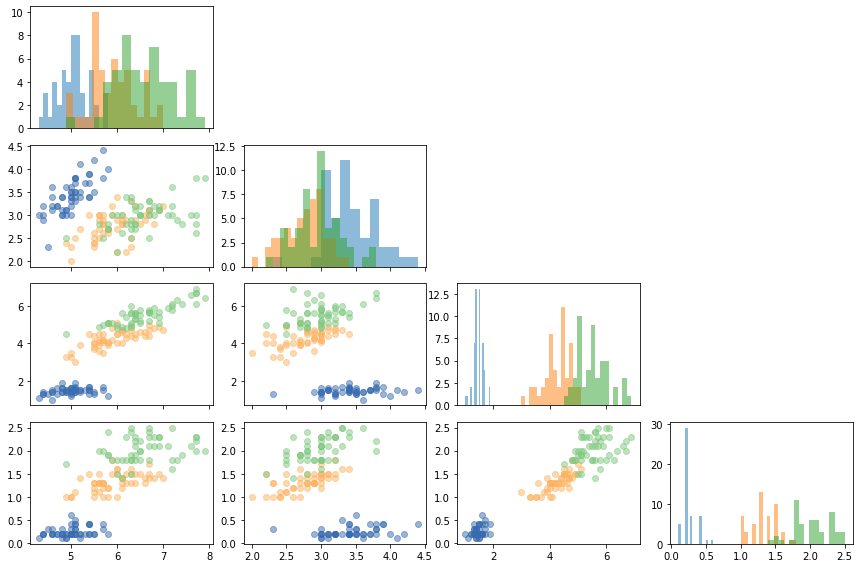
   

   

定制多样化的相关矩阵图

自定义相关矩阵图一般是结合使用场景对相关参数进行修改，并辅以其他的绘图知识。参数信息可以通过官网进行查看，其他的绘图知识则更多来源于实战经验，大家不妨将接下来的绘图作为一种学习经验，以便于日后总结。

seaborn主要利用pairplot绘制相关矩阵图，可以通过seaborn.pairplot了解更多用法

import seaborn as sns
import matplotlib.pyplot as plt

# 导入数据
df = sns.load_dataset('iris')

# 自定义参数
sns.pairplot(df, kind="scatter",  # 散点图，不带拟合线
                 hue="species",   # 对species进行分组（不同颜色）
                 plot_kws=dict(s=80, edgecolor="white", linewidth=2.5) # 自定义绘制参数
        )
plt.show()

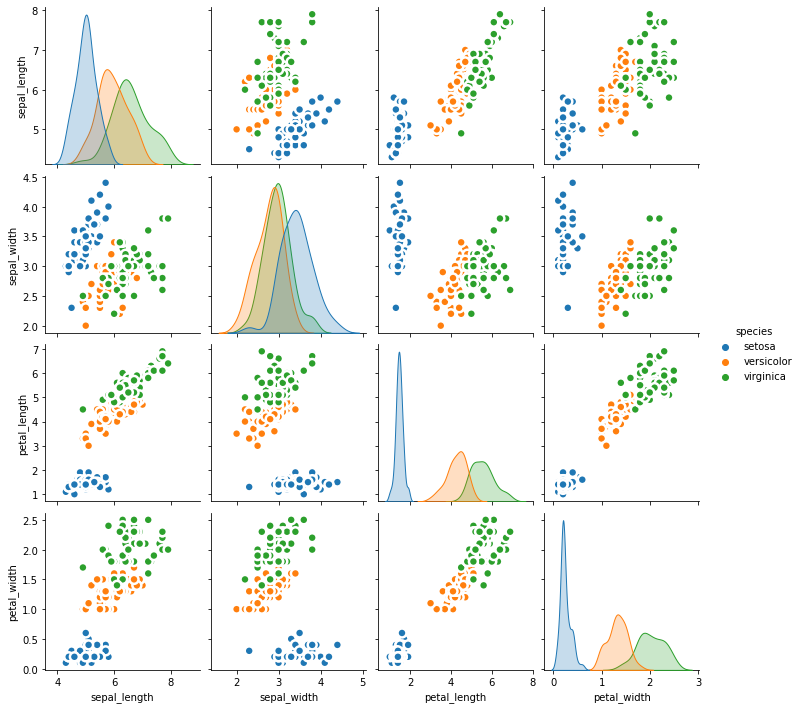
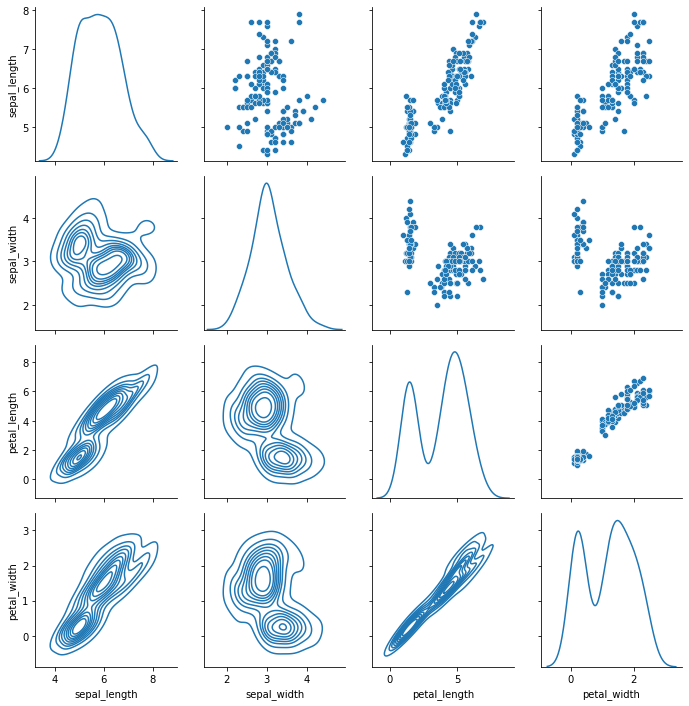
也可以利用PairGrid自定义更为灵活的相关矩阵图，可以通过seaborn.pairplot了解更多用法

import seaborn as sns
import matplotlib.pyplot as plt

# 导入数据
df = sns.load_dataset('iris')

g = sns.PairGrid(df, diag_sharey=False)
# 上三角散点图
g.map_upper(sns.scatterplot)
# 下三角密度图
g.map_lower(sns.kdeplot)
# 对角线密度图
g.map_diag(sns.kdeplot)

plt.show()

总结

以上通过seaborn的pairplot快速绘制相关矩阵图，也可以利用matplotlib自定义绘制相关矩阵图。并通过修改参数或者辅以其他绘图知识自定义各种各样的相关矩阵图来适应相关使用场景。

共勉～