算法专题课

北大硕士LeetCode算法专题课-栈、队列相关问题_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课--链表相关问题_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课-查找相关问题_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课-字符串相关问题_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课-数组相关问题_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课-基础算法查找_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课-基础算法之排序_骨灰级收藏家的博客-CSDN博客

北大硕士LeetCode算法专题课---算法复杂度介绍_骨灰级收藏家的博客-CSDN博客

二叉树简介

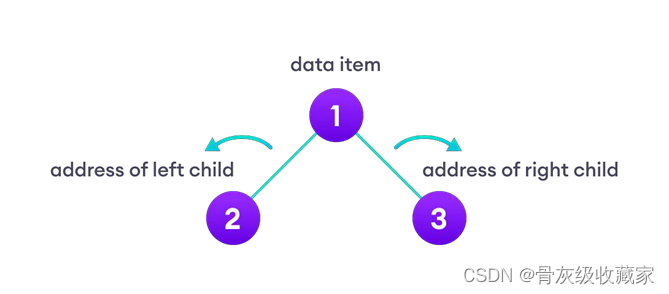
二叉树(Binary Tree) 是一种树形数据结构，其中每个父节点最多可以有两个子节点。 二叉树的每个节点（node）包含三个属性：

l  data 数据

l  left 左子节点的地址

l  right 右子节点的地址

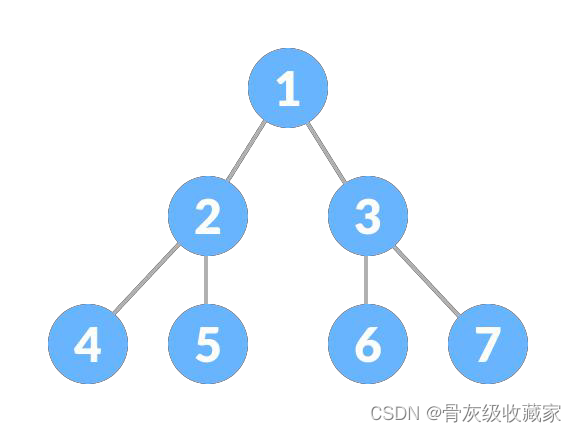
满二叉树(Full Binary Tree)：每个结点要么没有子结点，要么有两个子结点

 

完美二叉树(Pefect Binary Tree)：每个结点都有两个子结点，所有叶子结点都在同一层

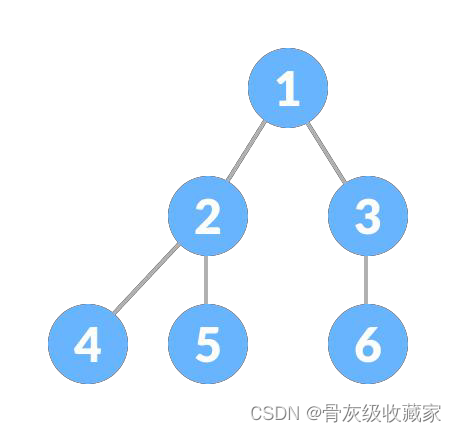
完全二叉树(Complete Binary Tree)：从根结点到倒数第二层为完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐

 

二叉树天然的具有递归结构，二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，  分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树 。

 

 

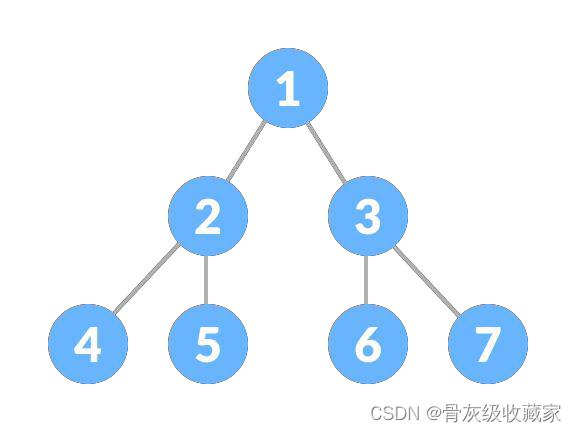
二叉树的遍历方式

LeetCode 题目中，二叉树的遍历方式是最基本，也是最重要的一类题目。先介绍一下二叉树的遍历方式。

先序遍历（前序遍历）：按照根节点 -> 左孩子 -> 右孩子 的方式遍历，即「先序遍历」，每次先遍历根节点，  遍历结果为 1 2 4 5 3 6 7；

 

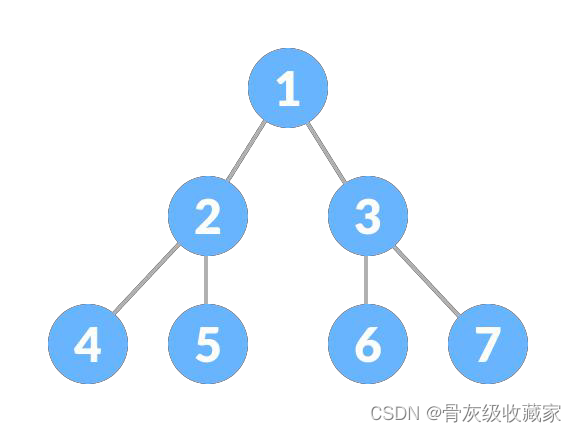
LeetCode 题目中，二叉树的遍历方式是最基本，也是最重要的一类题目。先介绍一下二叉树的遍历方式。 中序遍历：按照左孩子 -> 根节点 -> 右孩子 的方式遍历，即「中序序遍历」

遍历结果为 4 2 5 1 6 3 7；

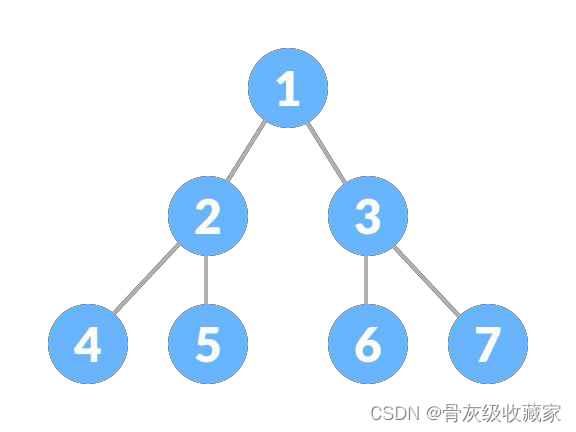
LeetCode 题目中，二叉树的遍历方式是最基本，也是最重要的一类题目。先介绍一下二叉树的遍历方式。 后序遍历：按照左孩子 -> 右孩子 -> 根节点 的方式遍历，即「后序序遍历」

遍历结果为 4 5 2 6 7 3 1；

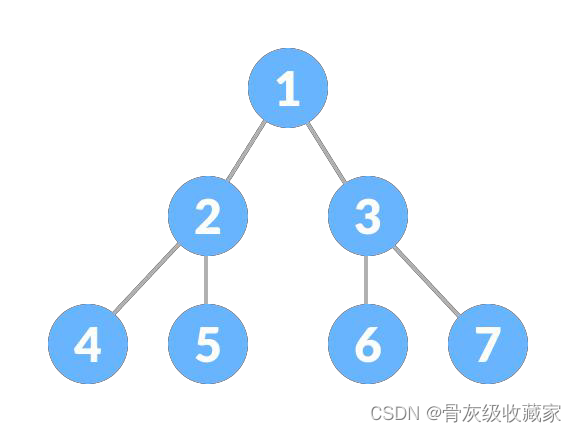
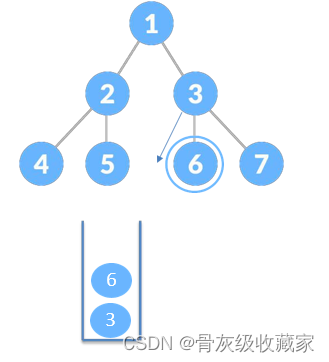
LeetCode 144.二叉树的前序遍历 输出结果 [1,2,4,5,3,6]

 

def preorderTraversal2(root):  res = list()
if not root:
return res

stack = []  node = root
while stack or node:
while node:
res.append(node.val)  stack.append(node)  node = node.left
node = stack.pop()  node = node.right
return res

二叉树的遍历解题方法- 迭代使用栈

LeetCode 144.二叉树的前序遍历 输出结果 [1,2,4,5,3,6,7]

def preorderTraversal2(root):  res = list()
if not root:
return res

stack = []  node = root
while stack or node:
while node:
res.append(node.val)  stack.append(node)  node = node.left
node = stack.pop()  node = node.right
return res

二叉树的遍历解题方法

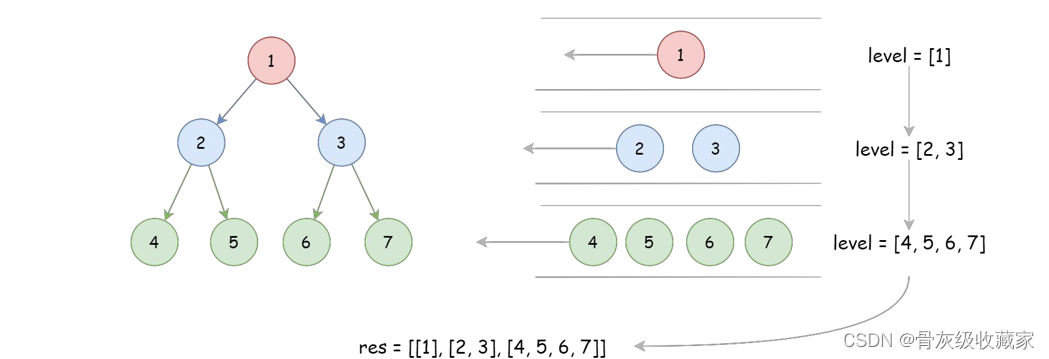
LeetCode 102 中等.二叉树的层序遍历，使用队列

输出结果 [[1], [2, 3], [4, 5, 6, 7]]

 

二叉树的最大深度 (LeetCode 104)

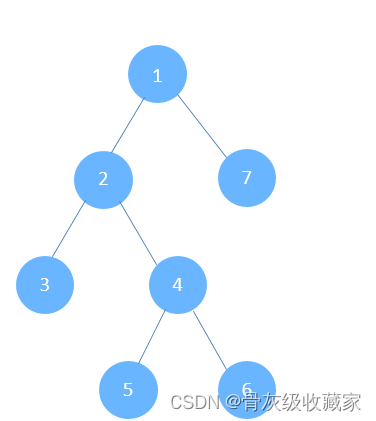
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。

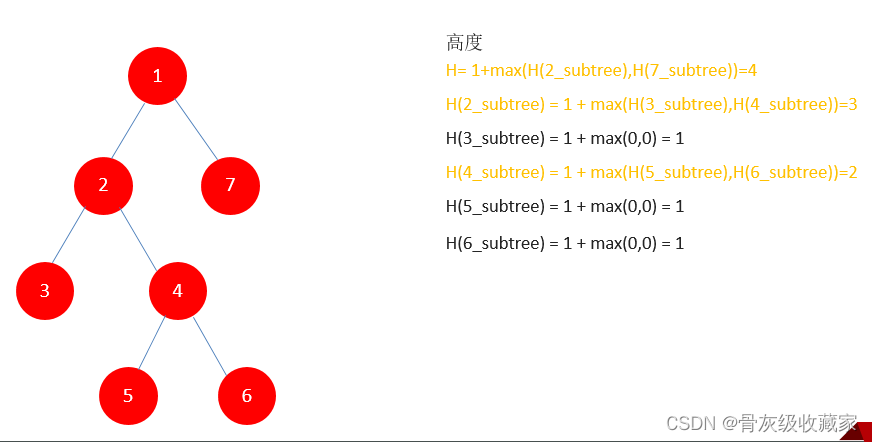
如果我们知道了左子树和右子树的最大深度 l和 r，那么该二叉树的最大深度即为 max(l,r)+1

 

如果我们知道了左子树和右子树的最大深度 l和 r，那么该二叉树的最大深度即为 max(l,r)+1

def maxDepth(root):  if root is None:
return 0
else:
left_height = maxDepth(root.left)  right_height = maxDepth(root.right)  return max(left_height, right_height) + 1

复杂度分析

时间复杂度：O(n) ，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。 空间复杂度：O(height) ，其中 height表示二叉树的高度。递归函数需要栈空间，而栈空 间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

翻转二叉树 (LeetCode 226)

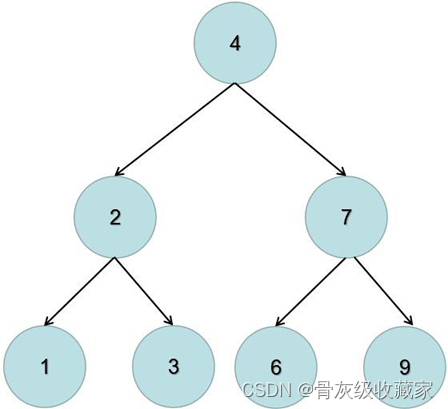
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

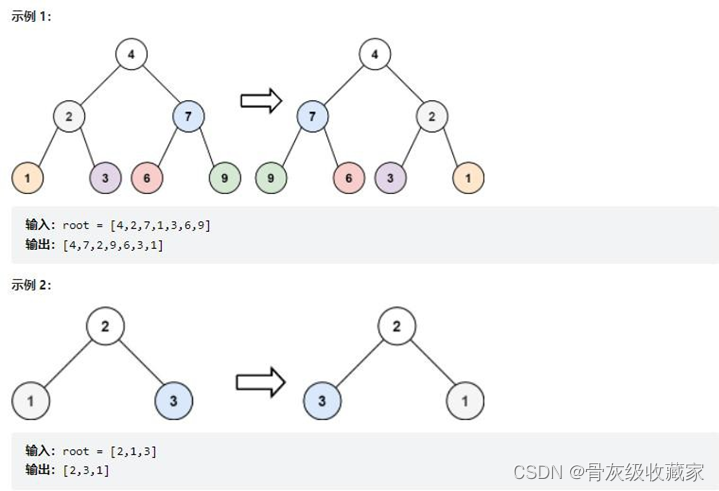
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

 给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。 

def invertTree(root):
# 递归终止条件，节点为空时返回
if not root:
return None
# 递归调用
left = invertTree(root.left)  right = invertTree(root.right)
# 将当前节点的左右子树交换 root.left, root.right = right, left  return root

复杂度分析：时间复杂度：O(n) 空间复杂度：O(n)

路径总和 (LeetCode 112)

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，  这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

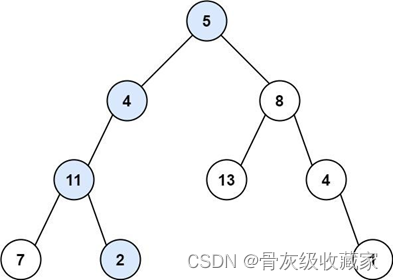
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22

输出：true

解释：等于目标和的根节点到叶节点路径如上图所示。

使用递归的思路解决问题的时候, 需要注意递归的终止条件。

class Solution(object):
def hasPathSum(self, root, targetSum):  """
:type root: TreeNode
:type targetSum: int
:rtype: bool  """
if not root:
return targetSum == 0
if self.hasPathSum(root.left, targetSum - root.val):
return True
if self.hasPathSum(root.right, targetSum - root.val):
return True
return False

 使用递归的思路解决问题的时候, 需要注意递归的终止条件。下面写法中的递归终止条件考虑并不全面，  当输入为[], targetSum = 0 时， 下面的解法会返回True， 但实际上应该是False

class Solution(object):
def hasPathSum(self, root, targetSum):  """
:type root: TreeNode
:type targetSum: int
:rtype: bool  """
if not root:
return targetSum == 0
if self.hasPathSum(root.left, targetSum - root.val):
return True
if self.hasPathSum(root.right, targetSum - root.val):
return True
return False

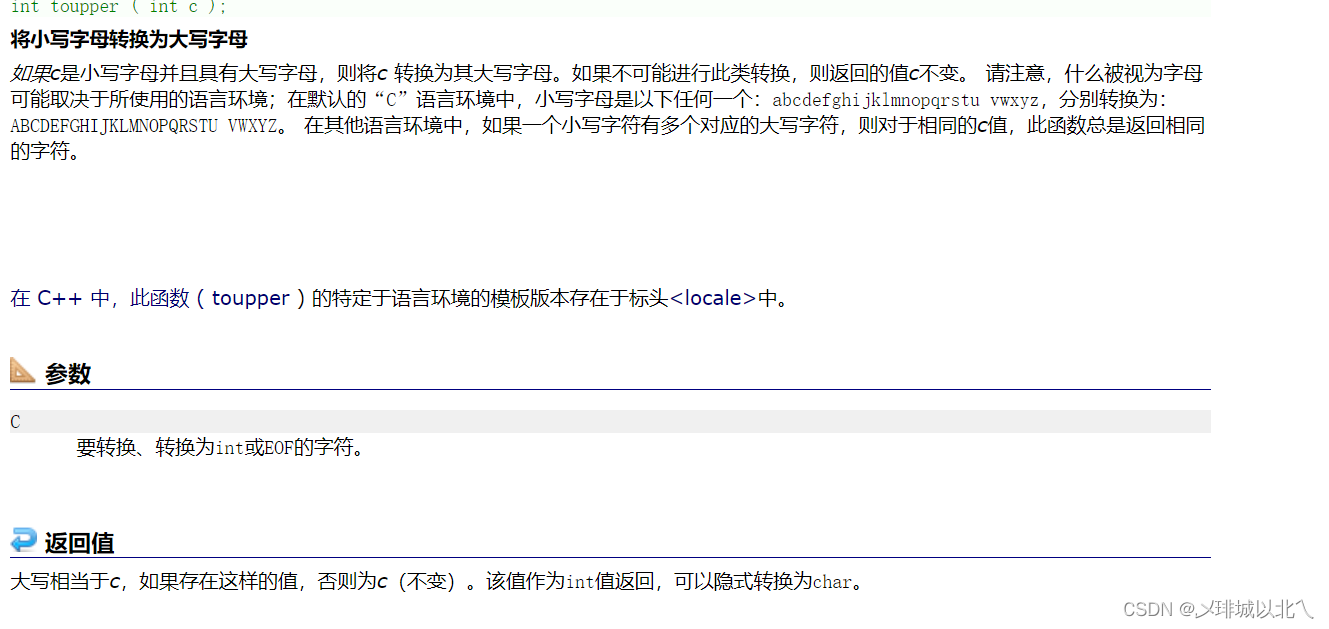
电话号码的字母组合 (LeetCode 17) 中等

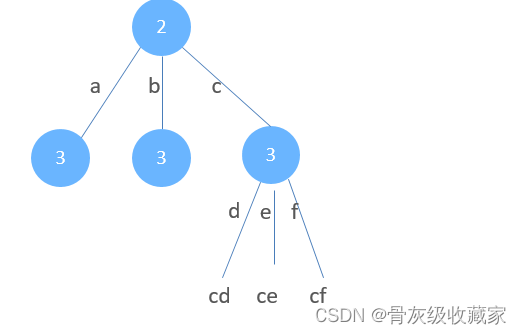
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

给给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

 

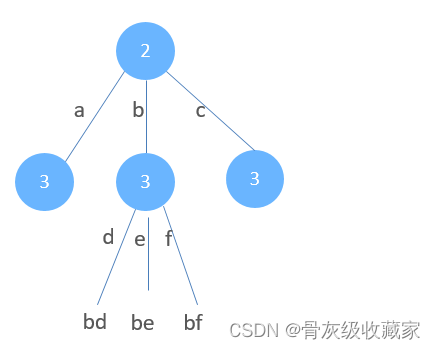
digits 是数字字符串, s(digits) 是 digits 所能代表的字母字符串

s(digits[0…n-1]) = letter(digits[0]) + s(digits[1…n-1]) = letter(digits[0]) + letter(digits[1]) + s(digits[2…n-1])

复杂度分析

时间复杂度：O(3n) (O(2n))

空间复杂度：O(m+n)

回溯法

回溯法也称试探法，它的基本思想是：

l  从问题的某一种状态（初始状态）出发，搜索从这种状态出发所能达到的所有“状态”，

l  当一条路走到“尽头”的时候（不能再前进），再后退一步或若干步，从另一种可能“状态”出发，继续搜索 直到所有的“路径”（状态）都试探过

l  这种不断“前进”、不断“回溯”寻找解的方法，就称作“回溯法”

回溯法是暴力解法的一个主要手段

全排列 (LeetCode 46) 中等

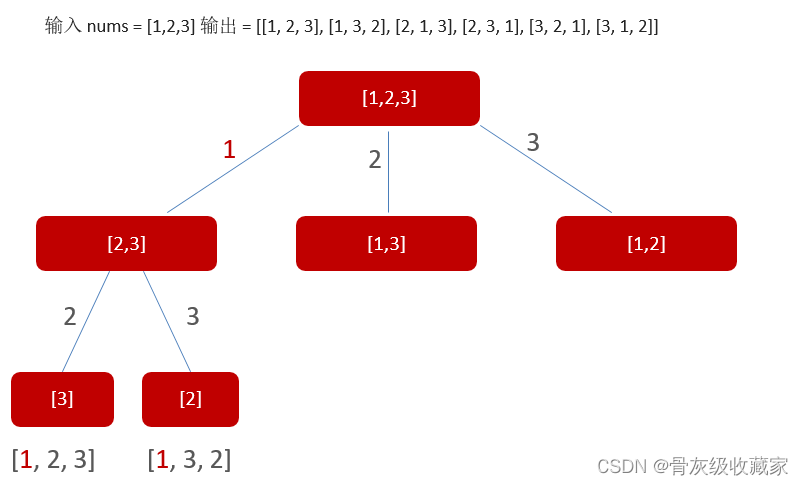
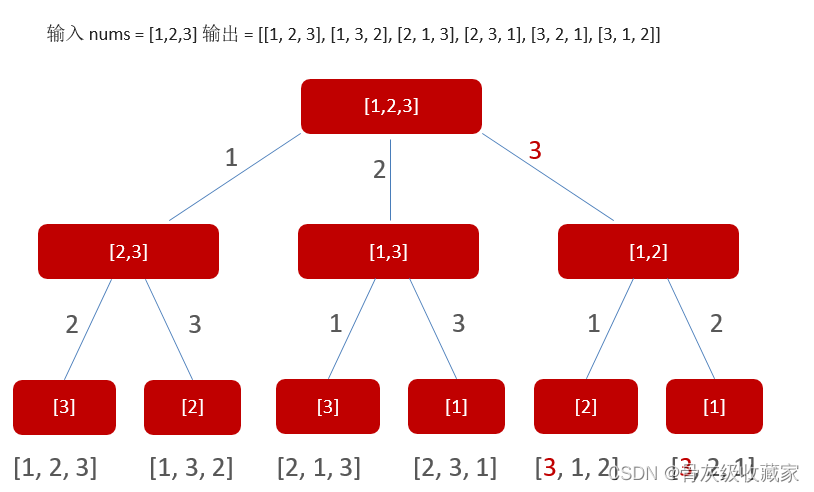
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

 

 

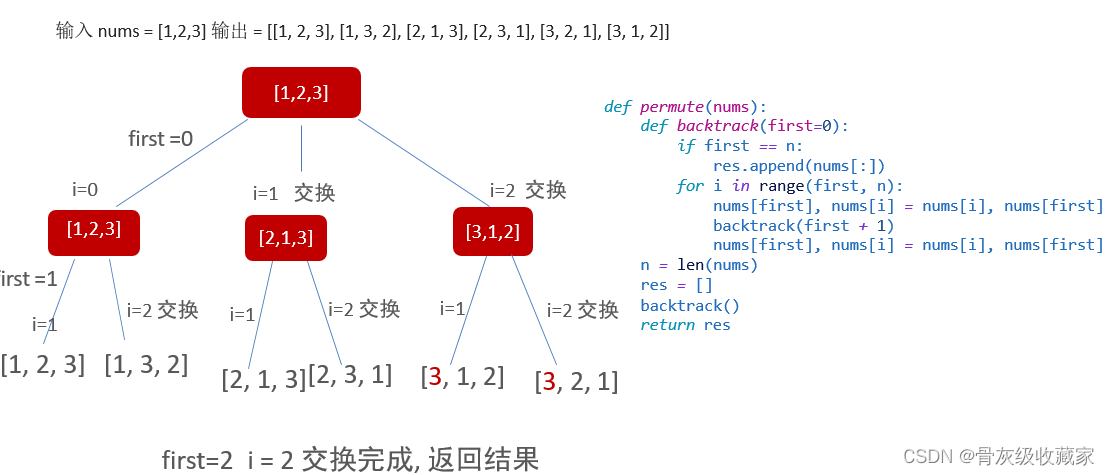
def permute(nums):
def backtrack(first=0):  if first == n:
res.append(nums[:])
for i in range(first, n):
nums[first], nums[i] = nums[i], nums[first]  backtrack(first + 1)
nums[first], nums[i] = nums[i], nums[first]  n = len(nums)
res = []  backtrack()  return res