一、map、set的底层结构
前面对map、set等树形结构的关联式容器进行了简单的介绍,了解到map、set都是由红黑树封装实现的。红黑树是一种由二叉搜索树进行平衡处理后的平衡树,其查找、插入、删除等操作的时间复杂度为O(logn),详情请参考数据结构——红黑树详解-CSDN博客。
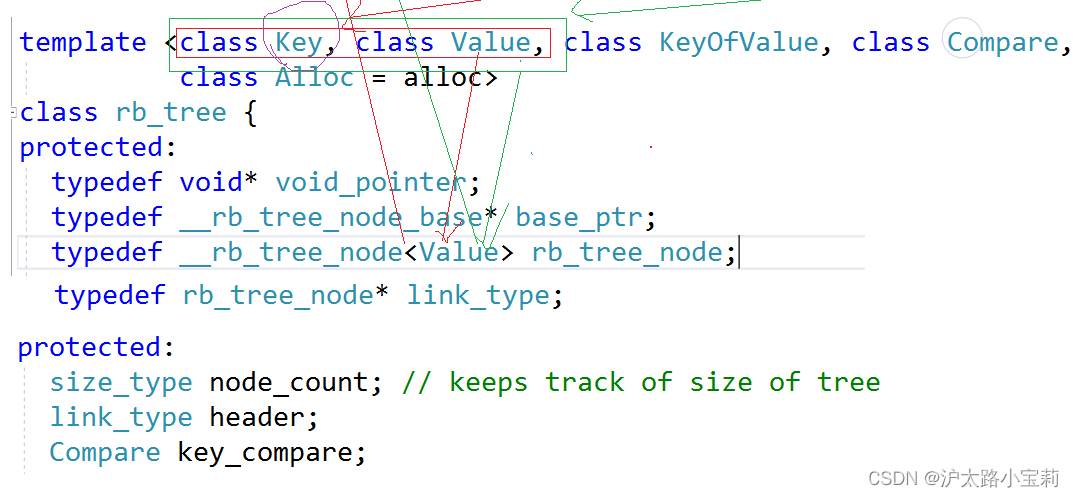
红黑树的类模板参数value
map、set底层都是使用红黑树进行封装,set内数据为key,只要传递K一个类模板参数;而map内数据为pair<key-value>键值对,需要传递K,V两个类模板参数给红黑树。那怎么解决这个问题呢?
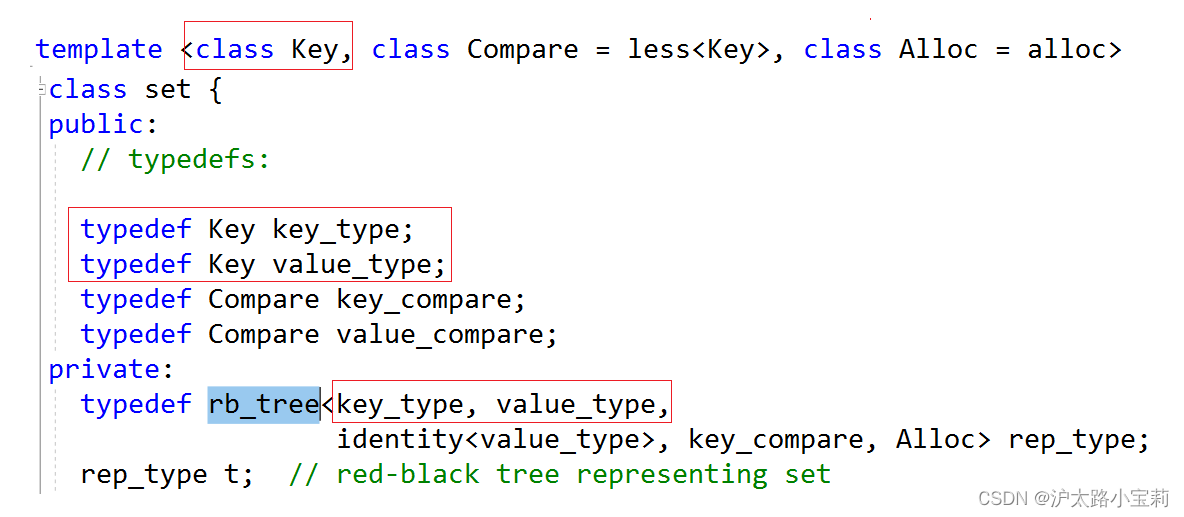

观察上图,set的类模板参数列表中只有一个Key,在内部将Key取别名为value_type。map的类模板参数列表中有Key、T,则是将Key、T构造为键值对后起别名为value_type。都将value_type类型传给红黑树的模板类参数列表,即由传递的value_type决定红黑树节点是set的key还是map的key-value,实现红黑树的泛型编程。
红黑树的类模板参数KeyOfValue
由于红黑数内数据类型的不确定,在查找,插入,删除等操作中,需要先取key值,再进行比较。所以我们需要向红黑树中传递KeyOfValue仿函数来进行取出key值的操作。
struct mapkeyofT {
const k& operator()(const pair<k, v>& kv) {
return kv.first;
}
};struct setkeyofT {
const k& operator()(const k& key) {
return key;
}
};
二、红黑树的迭代器实现
红黑树迭代器的本质就是红黑树的结点指针,要将红黑树中的元素升序遍历,我们采用中序遍历的方式来重载迭代器的++和--操作。
2.1 operator++与operator--
operator++(左子树、根、右子树)就是找到下一个只比当前元素大的元素。
如果当前节点右子树不为空,去找右子树中的最小值,即找到右子树的最左节点。
如果当前节点右子树为空,说明以当前节点为根节点的树中序遍历结束。依次向上查找直到祖先节点(parent)中左子树为cur的节点。
//按照中序遍历的方式,++
self& operator++() {
//如果右子树不为空,那么比这个元素大的下一个节点就是右子树的最小元素
//也就是右子树的最左节点
if (_node->_right)
{
Node* subleft = _node->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
_node = subleft;
}
else {//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中左子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur) {
//cur依旧为parent的右子树,说明更新后的cur中序遍历也结束了
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
operator--(右子树、根、左子树)就是找到下一个只比当前元素小的元素。
如果当前节点左子树不为空,去找左子树中的最大值,即找到左子树的最右节点。
如果当前节点左子树为空,说明以当前节点为根节点的树中序遍历结束。依次向上查找直到祖先节点(parent)中右子树为cur的节点。
//如果左子树不为空,那么比这个元素大的下一个节点就是左子树的最大元素
//也就是左子树的最右节点
self& operator--() {
if (_node->_left) {
Node* subright = _node->_left;
while (subright->_right) {
subright = subright->_right;
}
_node = subright;
}
else
{//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中右子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_left == cur) {
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
}2.2 operator==与operator!=
bool operator !=(const self& s) {
return _node != s._node;
}
bool operator==(const self& s) {
return _node = s._node;
}2.3 operator*与operator->
operator*()返回迭代器指向节点的数据,operator->()返回迭代器指向节点的数据的地址。
T& operator*() {
return _node->_data;
}
T* operator->() {
return &_node->_data;
}完整迭代器实现如下:
template<class T>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> self;
Node* _node;
RBTreeIterator(Node* node)
:_node(node)
{}
//运算符重载:那个对象调用符号,传那个对象的this指针
T& operator*() {
return _node->_data;
}
T* operator->() {
return &_node->_data;
}
//按照中序遍历的方式,++
self& operator++() {
//如果右子树不为空,那么比这个元素大的下一个节点就是右子树的最小元素
//也就是右子树的最左节点
if (_node->_right)
{
Node* subleft = _node->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
_node = subleft;
}
else {//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中左子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur) {
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
//如果左子树不为空,那么比这个元素大的下一个节点就是左子树的最大元素
//也就是左子树的最右节点
self& operator--() {
if (_node->_left) {
Node* subright = _node->_left;
while (subright->_right) {
subright = subright->_right;
}
_node = subright;
}
else
{//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中右子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_left == cur) {
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
}
bool operator !=(const self& s) {
return _node != s._node;
}
bool operator==(const self& s) {
return _node = s._node;
}
};三、红黑树的更改
之前已经对红黑树模拟实现,现在需要对红黑树进行一些更改方便map、set的封装。
3.1 红黑树的迭代器的封装
typedef RBTreeIterator<T> iterator;begin()与end()函数实现
begin()应该是一棵红黑树的最小节点,即最左节点;end()为nullptr。
iterator begin() {
Node* subleft = _root;
while (subleft && subleft->_left) {
subleft = subleft->_left;
}
return iterator(subleft);
}
iterator end()
{
return iterator(nullptr);
}
3.2 红黑树的查找、插入
在红黑树的查找、插入操作中,需要先实例化一个keyofT对象使用仿函数取出key值,再比较大小。另外,为了map的operator[],红黑树的插入函数返回值需要更改为<Iterator,bool>的键对值。
pair<iterator, bool> Insert(const T& data)
{
if (_root == nullptr) {
_root = new Node(data);
_root->_col = BLACK;
Node* newnode = _root;
return make_pair(iterator(newnode), true);
}
keyofT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (kot(cur->_data) < kot(data)) {
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);;
}
}
cur = new Node(data); // 在cur位置插入红色节点
Node* newnode = cur;
if (kot(parent->_data) < kot(data)) {//连接cur节点到红黑树
parent->_right = cur;
}
else {
parent->_left = cur;
}
cur->_parent = parent;
return make_pair(iterator(newnode), true);;
}上述为红黑树插入函数,忽略旋转、变色操作。
3.3 红黑树更改后代码实现
#define _CRT_SECURE_NO_WARNINGS
#pragma once
#include<vector>
#include<iostream>
#include<time.h>
using namespace std;
enum Colour {//枚举类型,红黑树颜色
RED,
BLACK
};
template<class T>//T决定节点是key还是k-v类型
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
template<class T>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> self;
Node* _node;
RBTreeIterator(Node* node)
:_node(node)
{}
//运算符重载:那个对象调用符号,传那个对象的this指针
T& operator*() {
return _node->_data;
}
T* operator->() {
return &_node->_data;
}
//按照中序遍历的方式,++
self& operator++() {
//如果右子树不为空,那么比这个元素大的下一个节点就是右子树的最小元素
//也就是右子树的最左节点
if (_node->_right)
{
Node* subleft = _node->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
_node = subleft;
}
else {//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中左子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur) {
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
//如果左子树不为空,那么比这个元素大的下一个节点就是左子树的最大元素
//也就是左子树的最右节点
self& operator--() {
if (_node->_left) {
Node* subright = _node->_left;
while (subright->_right) {
subright = subright->_right;
}
_node = subright;
}
else
{//右子树为空,(以当前节点为根节点的树中序遍历结束)向上查找
//下一个节点为祖先节点(parent)中右子树为cur的节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_left == cur) {
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
}
bool operator !=(const self& s) {
return _node != s._node;
}
bool operator==(const self& s) {
return _node = s._node;
}
};
template<class k, class T, class keyofT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef RBTreeIterator<T> iterator;
iterator begin() {
Node* subleft = _root;
while (subleft && subleft->_left) {
subleft = subleft->_left;
}
return iterator(subleft);
}
iterator end()
{
return iterator(nullptr);
}
pair<iterator, bool> Insert(const T& data)
{
if (_root == nullptr) {
_root = new Node(data);
_root->_col = BLACK;
Node* newnode = _root;
return make_pair(iterator(newnode), true);
}
keyofT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (kot(cur->_data) < kot(data)) {
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);;
}
}
cur = new Node(data); // 在cur位置插入红色节点
Node* newnode = cur;
if (kot(parent->_data) < kot(data)) {//连接cur节点到红黑树
parent->_right = cur;
}
else {
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
//1:当叔叔存在且为红
if (uncle && uncle->_col == RED)
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
//2:叔叔不存在或者存在且为黑,由第一种情况调整而来
//旋转+变色
if (cur == parent->_left)
{
// g
// p u
// c
//此时路径上黑色节点不相同,且有连续的红色节点,不满足最长路径是最短路径的两倍
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else {
// g
// p u
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_left;
// 情况一:叔叔存在且为红
if (uncle && uncle->_col == RED)
{
// 变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
// 情况二:叔叔不存在或者存在且为黑
// 旋转+变色
// g
// u p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else {
// g
// u p
// c
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);;
}
void RotateL(Node* parent)//左单旋
{
++rotateSize;
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL) {
subRL->_parent = parent;
}
subR->_left = parent;
Node* ppnode = parent->_parent;//记录parent的父节点
parent->_parent = subR;
if (parent == _root)//考虑parent是该树的根节点
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subR;
}
else
{
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
}
void RotateR(Node* parent)//右单旋
{
++rotateSize;
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR) {
subLR->_parent = parent;
}
subL->_right = parent;
Node* ppnode = parent->_parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subL;
}
else
{
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
}
size_t Size()
{
return _Size(_root);
}
size_t _Size(Node* root)
{
if (root == NULL)
return 0;
return _Size(root->_left)
+ _Size(root->_right) + 1;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
}
int GetRotateSize()
{
return rotateSize;
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
int Height()
{
return _Height(_root);
}
Node* Find(const k& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return NULL;
}
bool IsBalance()
{
if (_root && _root->_col == RED)
return false;
int refBlackNum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
refBlackNum++;
cur = cur->_left;
}
return Check(_root, 0, refBlackNum);
}
bool Check(Node* cur, int blackNum, int refBlackNum)
{//传blackNum,每次走到黑色节点++,为nullptr回到上一层调用走右子树,此时blackNum还是上一层的值
if (cur == nullptr) {
if (refBlackNum != blackNum) {
cout << "黑色节点的数量不相等" << endl;
return false;
}
return true;
}
if (cur->_col == RED && cur->_parent->_col == RED) {
cout << "存在连续的红色节点" << endl;
return false;
}
if (cur->_col == BLACK)
++blackNum;
return Check(cur->_left, blackNum, refBlackNum) && Check(cur->_right, blackNum, refBlackNum);
}
private:
Node* _root = nullptr;
int rotateSize = 0;
};四、map、set封装红黑树
4.1 set封装红黑树
set内部成员变量为实例化的红黑树对象,插入、查找等成员函数为调用红黑树对应函数。
template<class k>
class set
{
struct setkeyofT {
const k& operator()(const k& key) {
return key;
}
};
public:
typedef typename RBTree<k, k, setkeyofT>::iterator iterator;
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
pair<iterator, bool> insert(const k& key)
{
return _t.Insert(key);
}
private:
RBTree<k, k, setkeyofT> _t;
};
4.2 map封装红黑树
map内部成员变量为实例化的红黑树对象,插入、查找等成员函数为调用红黑树对应函数。
与set不同的是,map多了operator[]重载,它会在内部调用map的insert函数。
map的operator[]重载
v& operator[](const k& key)
{
pair<iterator, bool> ret = Insert(make_pair(key, v()));
return ret.first->second;//key对应节点迭代器指向的数据value
}insert函数会返回插入元素的迭代器位置和元素是否存在的bool值构成的pair对象,在operator[]函数中,会先让map对象调用insert函数插入键值k和value的默认值(为value类型的默认构造函数生成的临时对象)所构成的pair对象。
其中ret.first就是获取插入后元素的迭代器,ret.first->second获得key所对应的value值。
当key存在时,插入失败。获取key所在pair对象的迭代器,ret.first->second为key所对应的value。
当key不存在时,插入成功。获取新插入pair对象的迭代器,ret.first->second为默认value。
所以,map的operator[]能够实现查找,修改,插入三个功能。
map封装红黑树实现
template<class k, class v>
class map
{
struct mapkeyofT {
const k& operator()(const pair<k, v>& kv) {
return kv.first;
}
};
public:
typedef typename RBTree<k, pair<const k, v>, mapkeyofT>::iterator iterator;
//typedef创建了存在类型的别名,而typename告诉编译器RBTree<k, pair<const k, v>, mapkeyofT>::iterator是一个类型而不是一个成员。
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
pair<iterator, bool> insert(const pair<k, v>& kv)
{
return _t.Insert(kv);
}
v& operator[](const k& key)
{
pair<iterator, bool> ret = Insert(make_pair(key, v()));
return ret.first->second;//key对应节点迭代器指向的数据value
}
private:
RBTree<k, pair<const k, v>, mapkeyofT> _t;
};