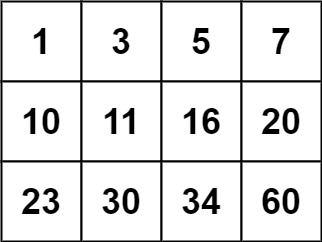
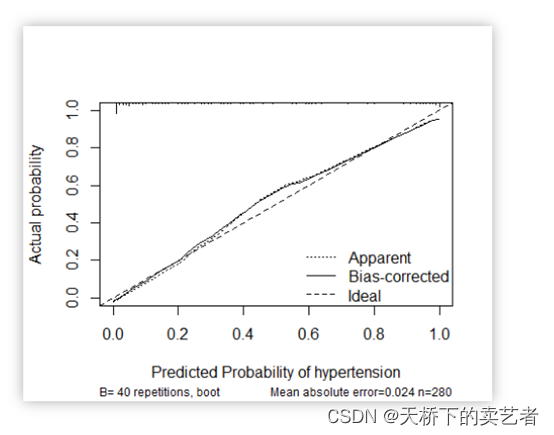
下面的图形是著名的杨辉三角形:
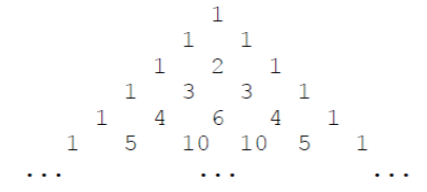
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
给定一个正整数 N,请你输出数列中第一次出现 N是在第几个数?
输入格式
输入一个整数 N。
输出格式
输出一个整数代表答案。
数据范围
对于 20% 的评测用例,1≤N≤10;
对于所有评测用例,1≤N≤10^9。
输入样例:
6
输出样例:
13题解:
杨辉三角是对称形状,所以每次求左边数字的位置及是第一次的位置,
按斜行看杨辉三角第一斜行为1(全为1),第二斜行为23456……第三斜行为6,10,15……
每一斜行的第一个数是C(k,2k)后面的依次为C(k,2k+1……)
由于题目范围最大10^9所以k最多到16.
每次枚举每一斜行,从2k开始到n(最晚会在C(n,1)的时候访问到这个值,这之后就不可能再找得到这个值了)二分枚举判断C(k,mid)与n关系
参考代码:
#include<iostream>
using namespace std;
typedef long long LL;
int n;
LL C (int a,int b)
{
LL res = 1;
for(int i = a,j = 1;j<=b;j++,i--)
{
res = res*i/j;
if(res>n) return res;//证明在这一斜行的数都是>n;
}
return res;
}
bool check(int k)
{//二分:
LL l = 2*k, r = n;//每一斜行第一个数(也是最小数)都是C(k,2k),这里的check函数就是找到合适的“底数”,所以从2k开始寻找。
if(l>r) return false;//特例:否则当n=1时,会出问题!
//注:当n=1时,k从16往下检查时,当k=1时,l=2k,r=n=1,因为l>r,会直接跳出二分的while循环
//C(r,k)=C(1,1)=1。根据C(1,1)得到的顺序值,此时就会输出1的位置是3,但是这个位置不是第一次出现的位置。正确的位置应该是(0,0)
while(l<r)
{
LL mid = (l+r)>>1;
if(C(mid,k)>=n) r = mid;
else l = mid+1;
}
if(C(r,k)!=n) return false;
printf("%lld\n",r*(r+1)/2+k+1);//r前面有r行(横着,第一个单独1算第一行,k前面有k个数+1就是自己的位置)
return true;
}
int main()
{
scanf("%d",&n);
for(int k = 16; ; k--)
if(check(k))
break;
return 0;
}