数字三角形（线性dp）-java

news2025/1/31 8:03:48

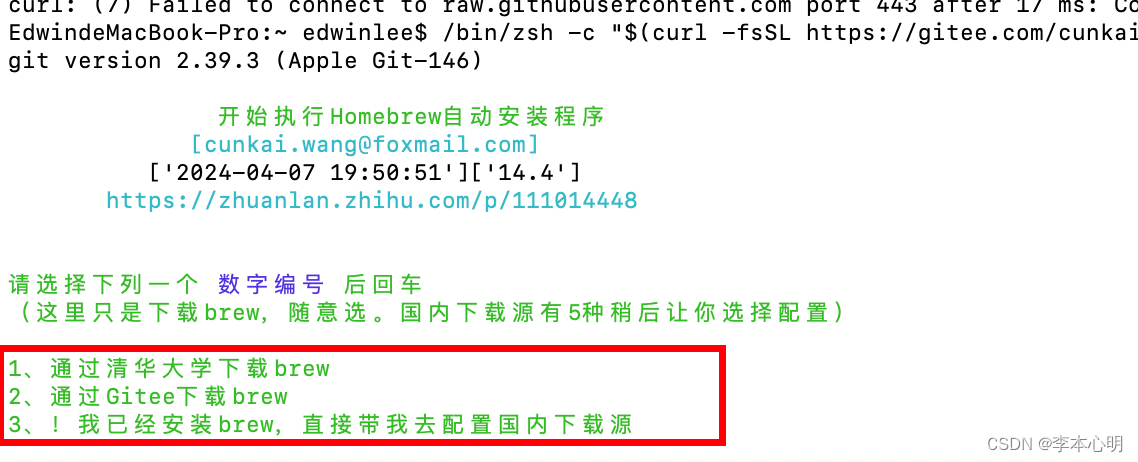
线性DP是动态规划问题中的一类问题，指状态之间有线性关系的动态规划问题。

文章目录

前言

一、数字三角形问题

二、算法思路

三、使用步骤

1.代码如下（示例）：

2.读入数据

3.代码运行结果

总结

前言

线性DP是动态规划问题中的一类问题，指状态之间有线性关系的动态规划问题。

提示：以下是本篇文章正文内容，下面案例可供参考

一、数字三角形问题

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

二、算法思路

图 1.1样例图

我们引入把数据分为5行，然后按照斜方向算一列进行存储数据。例数字6所在的位置为(5,4)。引入一个二维数组a[i][j]来存储每一个点上的数值。

我们引入dp数组，dp[i][j]表示所有从起点走到（i,j）的路径的数字之和的最大值

我们以图中的(2,7)的数字7为例，如果要实现到数字7的路径的数字的最大值，那么就是从左上和右上的两种情况中取最大值即：

图1.2样例模拟图

故dp[i][j]的递推公式为：

$dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j]$

整个dp状态数组的数据如下：

0 0  0  0  0  0 
0 7  0  0  0  0 
0 10 15 0  0  0 
0 18 16 15 0  0 
0 20 25 20 19 0 
0 24 30 27 26 24

三、使用步骤

1.代码如下（示例）：



import java.io.*;
public class 数字三角形 {
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) throws Exception{
        int n = nextInt();
        int[][] a = new int[510][510];
        int[][] dp = new int[510][510];
        //录入数据
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= i;j++){
                a[i][j] = nextInt();
            }
        }
        //dp数组初始化
        for (int i = 0; i <= n;i++){
            for(int j = 0;j <= i+1;j++){
                dp[i][j] = Integer.MIN_VALUE;
            }
        }
        //构建dp数组
        dp[1][1] = a[1][1];
        for (int i = 2; i <= n;i++){
            for(int j = 1;j <= i;j++){
                dp[i][j] = a[i][j]+Math.max(dp[i-1][j-1],dp[i-1][j]);
            }
        }
        int res = Integer.MIN_VALUE;
        //dp数组的最后一行表示我们从起点走到最后一行底部的各各最大值，找出其中最大的即可
        for(int j = 1;j <= n;j++){
            res = Math.max(res,dp[n][j]);
        }
        pw.println(res);
        pw.flush();
    }
    public static int nextInt()throws Exception{
        st.nextToken();
        return (int)st.nval;
    }
}