目录
题目链接
颜色分类
算法原理
代码实现
排序数组
算法原理
代码实现
最小的k个数
算法原理
代码实现
题目链接
LeetCode链接:75. 颜色分类 - 力扣(LeetCode)
LeetCode链接:912. 排序数组 - 力扣(LeetCode)
LeetCode链接:面试题 17.14. 最小K个数 - 力扣(LeetCode)
颜色分类

算法原理
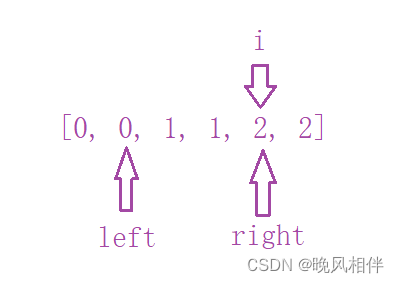
我们可以将这个数组划分为三个区域,左边区域全是0也就是红色,中间区域全是1也就是白色,右边区域全是2也就是蓝色。因此我们可以用个变量i来遍历数组,变量left标记0(红色)区域的最右侧,变量right标记2(蓝色)区域的最左侧。
那么就会形成下图所示区域
- [0, left]:全都是0
- [left + 1, i - 1]:全都是1
- [i, right - 1]:全都是待遍历的元素
- [right, n - 1]:全都是2

在遍历数组的时候分情况讨论
- 当nums[i] == 0时:我们需要将 i 位置的元素和 left + 1位置的元素进行交换,这样就能保证在left的左边都是0(包括left),,交换完后i向后移动,swap(nums[++left], nums[i++]。
- 当nums[i] == 1时:直接i++,这样就能保证left + 1到i这个区域内都是1。
- 当nums[i] == 2时:我们需要将 i 位置的元素和 right - 1位置的元素进行交换,这样就能保证在right的右边都是2(包括right),此时的 i 不需要移动,因为 i 到 right - 1 的这块区域都是待遍历的元素,交换后还是待遍历的元素。swap(nums[--right], nums[i])。
当i >= right时停止遍历
代码实现
class Solution {
public:
void sortColors(vector<int>& nums) {
int i = 0, n = nums.size();
int left = -1, right = n;
while(i < right)
{
if(nums[i] == 0)
{
swap(nums[++left], nums[i++]);
}
else if(nums[i] == 1)
{
i++;
}
else
{
swap(nums[--right], nums[i]);
}
}
}
};排序数组

算法原理
和上面颜色分类的思想是一样的,将数组划分为三块区域,左边区域为小于key的,中间区域为等于key的,右边区域为大于key的。
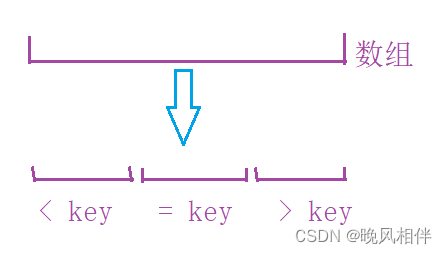
分类讨论:
- 当nums[i] < key时:我们需要将 i 位置的元素和 left + 1 位置的元素进行交换,这样就能保证在left的左边全都是比key小的数(包括left),交换完后i向后移动,swap(nums[++left], nums[i++]。
- 当nums[i] == key时:直接i++,这样就能保证left + 1到i这个区域内都是等于key的。
- 当nums[i] > key时:我们需要将 i 位置的元素和 right - 1位置的元素进行交换,这样就能保证在right的右边都是大于key的(包括right),此时的 i 不需要移动,因为 i 到 right - 1 的这块区域都是待遍历的元素,交换后还是待遍历的元素。swap(nums[--right], nums[i])。
小优化:可以选择随机的方式来选择key值,至于为什么可以去看看算法导论这本书,里面给出了详细证明。
代码实现
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
srand(time(nullptr));
qsort(nums, 0, nums.size() - 1);
return nums;
}
void qsort(vector<int>& nums, int l, int r)
{
if(l >= r) return;
int key = getRandom(nums, l, r);//随机取key值
//分三块区域
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(nums[i] < key) swap(nums[++left], nums[i++]);
else if(nums[i] == key) i++;
else swap(nums[--right], nums[i]);
}
//递归
qsort(nums, l, left);
qsort(nums, right, r);
}
int getRandom(vector<int>& nums, int left, int right)
{
int r = rand();
return nums[r % (right - left + 1) + left];
}
};最小的k个数
算法原理
原理和上面的排序数组一样,只是在最后要进行讨论一下k的大小

分类讨论:
- 如果c >= k:k是落在大于key的这个区域内,只需递归这个区域找出key即可。
- 如果b + c >= k:直接返回key就行了,因为k就落在了等于key的这个区域内。
- 如果上面两种情况都不满足,那说明k落在了小于key这个区域内,只需找k - b - c(要把前面两个的区域去掉)大的并且递归这个区域即可。
代码实现
class Solution {
public:
int getRandom(vector<int>& arr, int left, int right)
{
return arr[rand() % (right - left + 1) + left];
}
void qsort(vector<int>& arr, int l, int r, int k)
{
if(l >= r) return;
int key = getRandom(arr, l, r);
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(arr[i] < key) swap(arr[++left], arr[i++]);
else if(arr[i] == key) i++;
else swap(arr[--right], arr[i]);
}
int a = left - l + 1, b = right - left - 1;
if(a >= k) qsort(arr, l, left, k);
else if(a + b >= k) return;
else qsort(arr, right, r, k - a - b);
}
vector<int> smallestK(vector<int>& arr, int k) {
srand(time(nullptr));
qsort(arr, 0, arr.size() - 1, k);
return {arr.begin(), arr.begin() + k};
}
};今天的内容就分享到这里了,如果内容有错,有写的不好的地方,还望告知,谢谢!!!