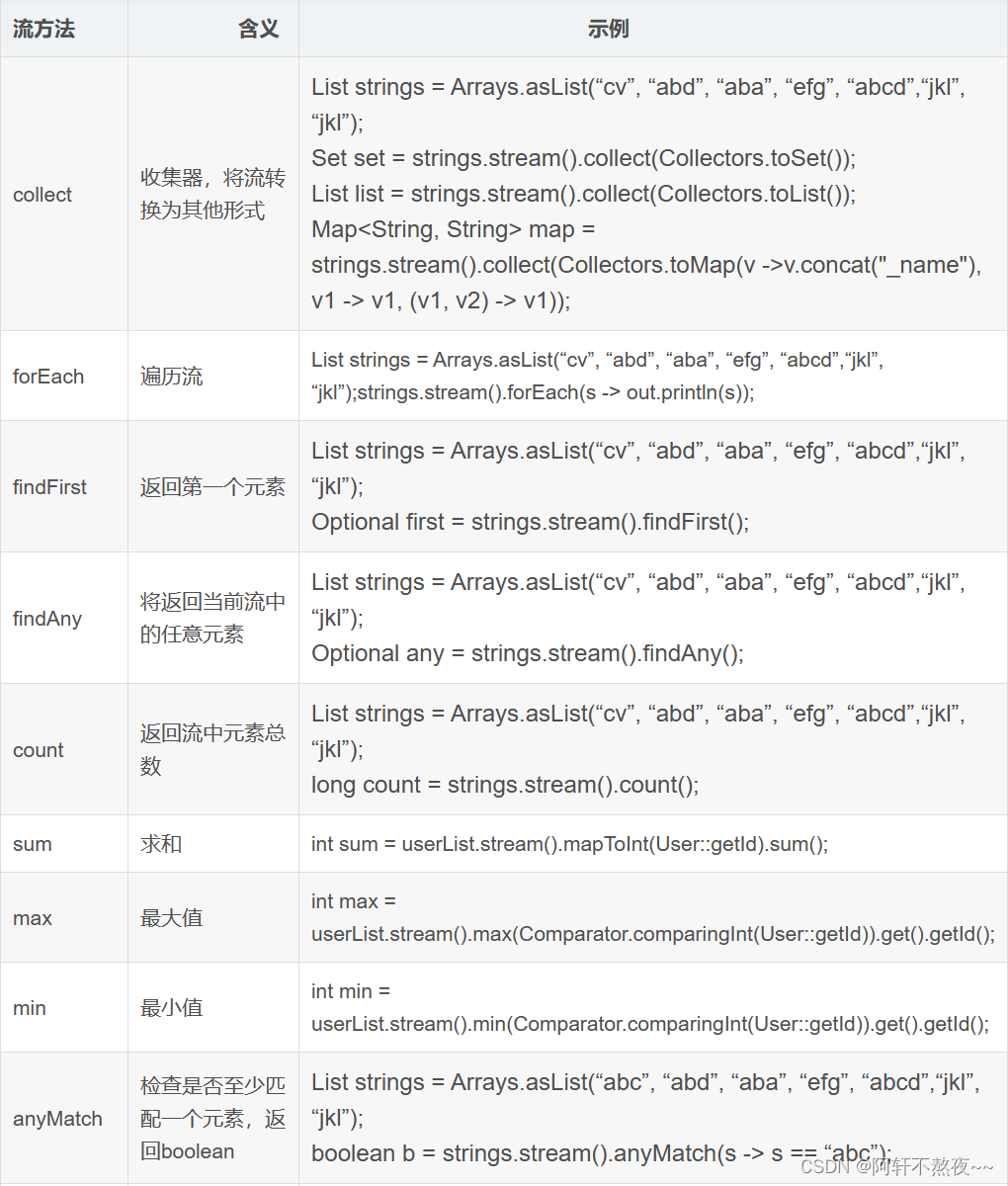
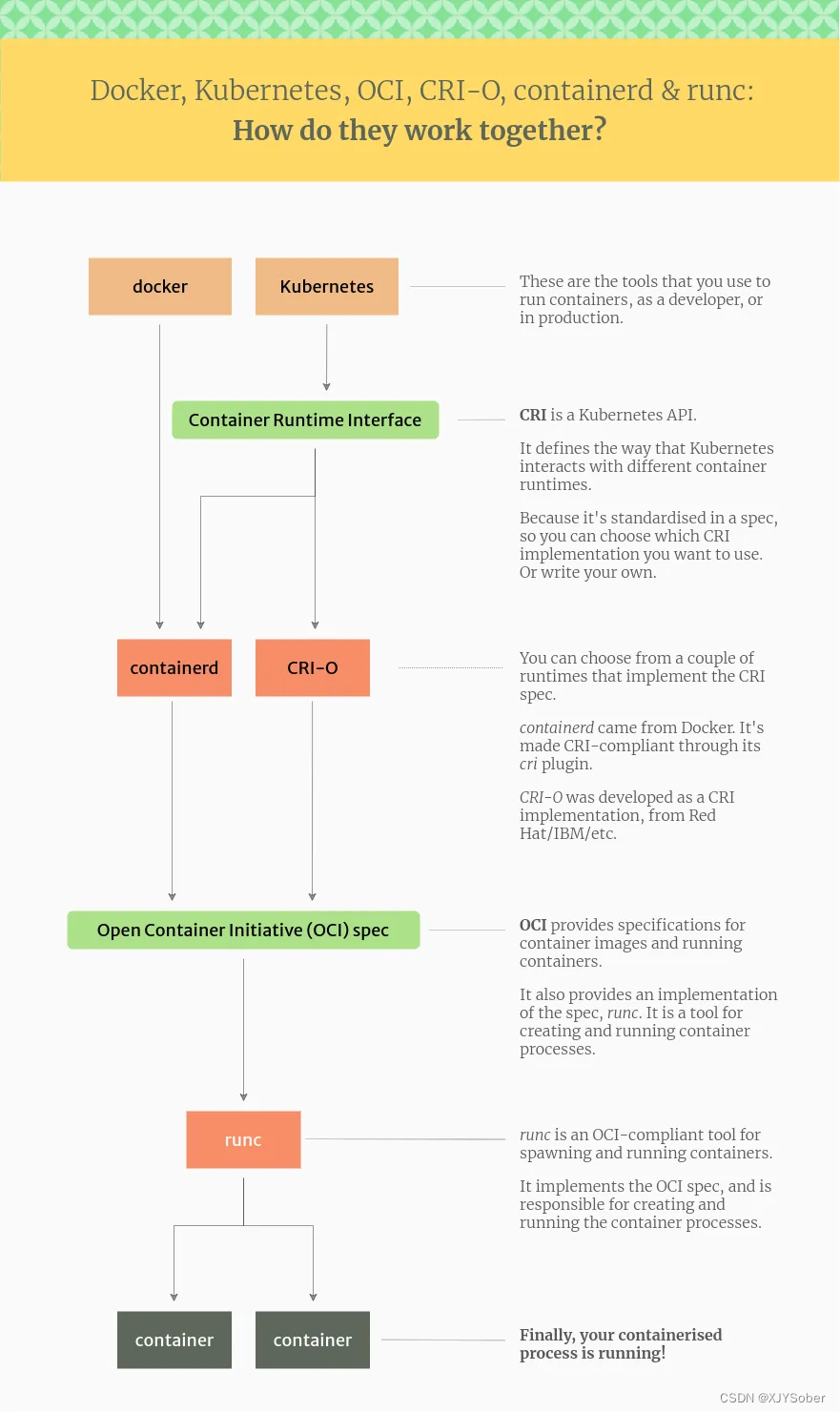
目录
1 70. 爬楼梯
1.1 基本思路
1.2 官方题解
2 118. 杨辉三角
3 198. 打家劫舍
菜鸟做题,语言是 C++
1 70. 爬楼梯
核心思想:把总问题拆解为若干子问题。
- 总问题:上到 5 楼的方式有多少种
- 子问题:上到 4 楼的方式有多少种、上到 3 楼的方式有多少种
- 总问题 = 子问题 1 + 子问题 2
因为题目要求每次只能爬 1 或 2 个台阶,所以子问题只有两个。
1.1 基本思路
假设按照英国算法要爬 6 层楼,如下图所示:
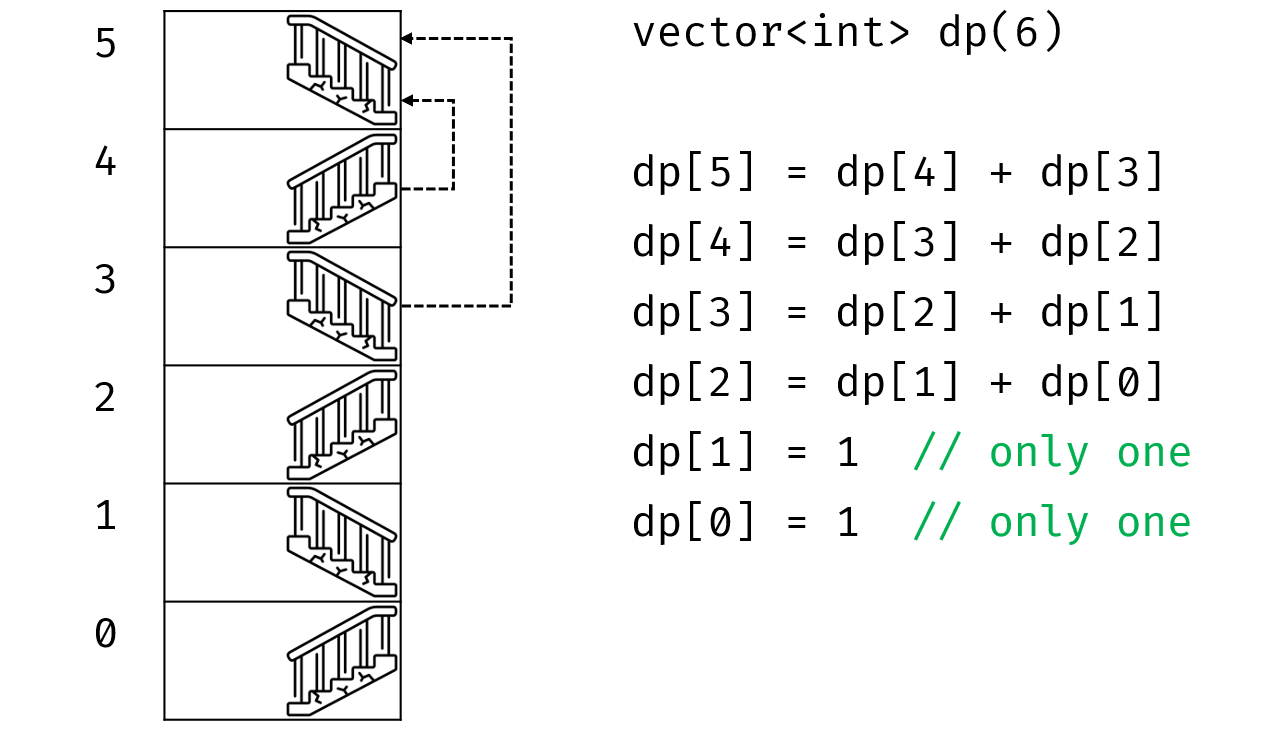
使用一个名为 dp 的数组来存储爬到每一层楼的方式种数。
由于我们只能从 4 或 3 楼爬到 5 楼,因此爬到 5 楼的方式种数 = 爬到 4 楼的方式种数 + 爬到 3 楼的方式种数,即 dp[5] = dp[4] + dp[3],以此类推。
特别地,对于 0 楼和 1 楼,由于只有一种方式爬到它们,因此直接设为 1 即可。
很不幸,上述方法需要维护一个长为 n 的数组 dp,因此空间复杂度是 O(n),而这样会超出内存限制,下面来看官方题解的奇妙方法。
1.2 官方题解
由 1.1 节的分析可知,dp[5] 只与 dp[4] 和 dp[3] 有关。因此在第 5 时刻,我们只需要记住 dp[4] 和 dp[3] 即可。换句话说,就是通过忘记其他 dp 元素来节省内存空间。
如下图所示。我们设置变量 p、q、r 来分别存储 dp[i - 2]、dp[i - 1]、dp[i],并不断更新这些变量。

可以把 p、q、r 理解为一个滑动窗口,每次同时向后移动一格,以此忘记不再需要的 dp 元素。
完整代码如下:
class Solution {
public:
int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 0; i < n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
};这个启动方式还是挺妙的:
int p = 0, q = 0, r = 1;2 118. 杨辉三角
核心思想:把总问题拆解为若干子问题。
- 总问题:第 i 行第 j 列元素的值
- 子问题:第 i - 1 行第 j 列元素的值、第 i - 1 行第 j + 1 列元素的值
- 总问题 = 子问题 1 + 子问题 2
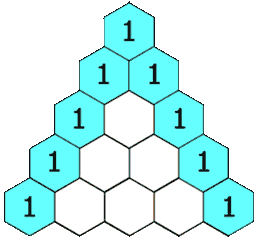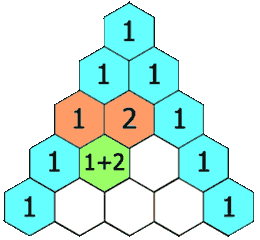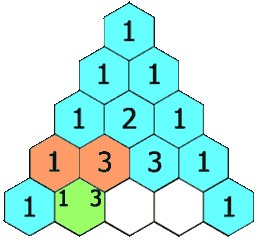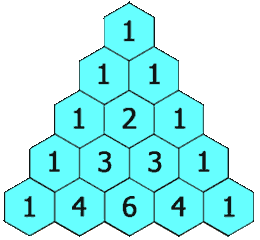
模仿上述动图初始化 ans 数组:
vector<vector<int>> ans(numRows);
for (int i = 1; i <= numRows; ++i) {
ans[i - 1].resize(i);
ans[i - 1][0] = 1;
ans[i - 1][i - 1] = 1;
}就是把那一圈 “1” 先填了,虽然笨,但貌似不影响效率。
完整代码如下:
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans(numRows);
for (int i = 1; i <= numRows; ++i) {
ans[i - 1].resize(i);
ans[i - 1][0] = 1;
ans[i - 1][i - 1] = 1;
}
for (int i = 2; i < numRows; ++i) {
for (int j = 1; j < ans[i].size() - 1; ++j) {
ans[i][j] = ans[i - 1][j - 1] + ans[i - 1][j];
}
}
return ans;
}
};3 198. 打家劫舍
核心思想:把总问题拆解为若干子问题。
- 总问题:打劫完第 i 家所获最大金额
- 子问题:打劫完第 i - 2 家所获最大金额、打劫完第 i - 3 家所获最大金额
- 总问题 = 子问题 1 + 子问题 2
Q:为什么只考虑打劫第 i - 2 家和第 i - 3 家?
A:假设 i = 5,如下图所示。对于第 i - 1 家,由于不能打劫相邻的两家,因此要想打劫第 i 家,就不能打劫第 i - 1 家。可以打劫第 i - 2 家或者第 i - 3 家,如情况一和情况二所示。对于第 i - 4 家,由于要使金额最大,因此肯定还会打劫第 i - 2 家,从而认为情况一等价于情况三。
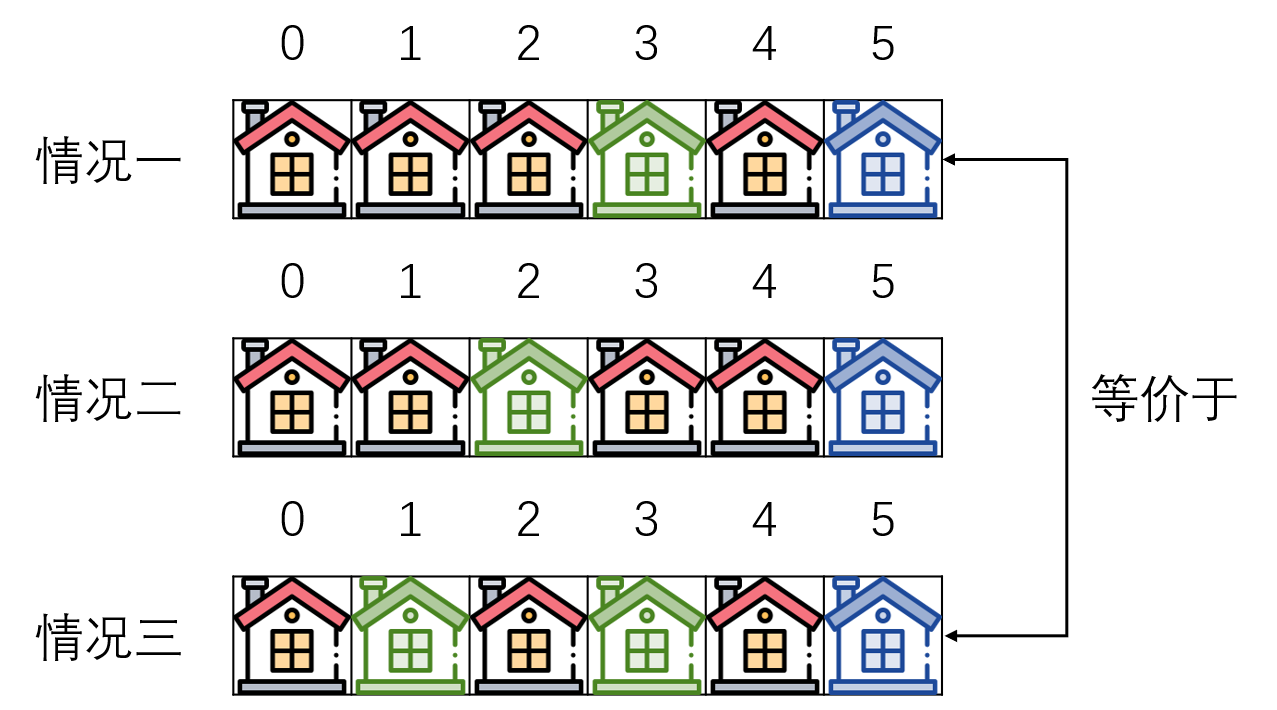
综上,我们只需要考虑情况一和情况二即可。
同 70. 爬楼梯 的简化思路相同,我们同样可以只设置几个变量来存储历史打劫金额,而非使用一个 dp 数组。其中,h3 存储第 i - 3 家,h2 存储第 i - 2 家,h1 存储第 i - 1 家,h0 存储第 i 家。
完整代码如下:
class Solution {
public:
int rob(vector<int>& nums) {
int h3 = 0, h2 = 0, h1 = 0;
int ans = INT_MIN;
for (int i = 0; i < nums.size(); ++i) {
int h0 = max(nums[i] + h3, nums[i] + h2);
ans = max(ans, h0);
h3 = h2;
h2 = h1;
h1 = h0;
}
return ans;
}
};