二分查找与搜索树高频问题-算法通关村
1 基于二分查找的拓展问题
1.1 山脉数组的封顶索引
-
LeetCode852:这个题的要求有点啰嗦,核心意思就是在数组中的某位位置i开始,从0到 i 是递增的,从i+1到数组最后是递减的,让你找到这个最高点。
详细要求是:符合下列属性的数组 arr 称为山脉数组:arr.length >= 3存在i(0 < i < arr.length - 1) 使得:
• arr[0] < arr[1] < … arrli-1] < arr[i]
• arrli] > arrli+1]>.>arrlarr.length - 1]
给你由整数组成的山脉数组 arr,返回任何满足 arr[0] < arr[1]< … arr[i- 1] < arr[i] > arr[i +1] >……>arrlarr.length - 1]的下标 i 。 -
这个题最简单的方式是对数组进行一次遍历。
当我们遍历到下标i时,如果有arr[i-1]< arr[i] > arr[i+1] ,那么 i 就是我们需要找出的下标。
其实还可以更简单一些,因为是从左开始找的,开始的时候必然是 arr[i-1] < a[i],所以只要找到第一个arrlil>arrli+1]的位置即可。代码就是: -
//时间复杂度是 O(n) public int peakIndexMountainArray(int[] arr){ int n = arr.length; for(int i = 0; i < n; i++){ if(arr[i] > arr[i+1]){ return i; } } return -1; } -
这个题能否使用二分来优化一下呢?当然可以。
对于二分的某一个位置 mid,mid 可能的位置有3种情況:- mid在上升阶段的时候,满足 arr[mid] > arr[mid-1] && arr[mid] < arr[mid+1]
- mid在顶峰的时候,满足 arr[i] > arr[i-1] && arr[i] > arr[i+1]
- mid在 下降阶段,满足 arr[mid]< a[mid-1] && arr[mid]> arr[mid+1] 因此我们根据 mid 当前所在的位置,调整二分的左右指针,就能找到顶峰。
-
//时间复杂度是 O(log n) public int peakIndexMountainArray(int[] arr){ if(arr.length == 3){ return 1; } //数组的第一个元素(索引为0)和最后一个元素 // (索引为 arr.length - 1)都不会是山峰 int left = 1; int right = arr.length-2; while(left < right){ int mid = left + ((right-left) >> 1); if(arr[mid] > arr[mid-1] && arr[mid] > arr[mid+1]){ return mid; } if(arr[mid] > arr[mid-1] && arr[mid] < arr[mid+1]){ left = mid+1; } if(arr[mid] < arr[mid-1] && arr[mid] > arr[mid+1]){ right = mid-1; } } return left; }
1.2 旋转数字的最小数字
-
我们说刷算法要按照专题来刷,这样才能看清很多题目的内在关系,二分查找也是如此,很多题目看似与二分无关,但是就是在考察二分查找。
-
LeetCode153 :已知一个长度为 n 的数组,预先按照升序排列,经由1到n次旋转后,得到输入数组。例如原数组 nums = [0, 1, 2, 4, 5, 6, 7] 在变化后可能得到:
- 若旋转 4次,则可以得到 [4, 5, 6, 7, 0, 1, 2]
- 若旋转7次,则可以得到 [O, 1, 2, 4, 5, 6, 7]
注意,数组 [ nums[0],nums[1],nums[2]…nums[n-1] ] 旋装一次的結果数 [nums[n-1], nums[0], nums[1],nums[2],…,nums[n-2]]。
-
示例1:
输入:nums = [4, 5 , 1, 2, 3]
输出:1
解释:原数组为 [1,2,3,4,5」,旋转 3 次得到输入数组。
示例2:
輸入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7],旋转 4 次得到输入数组。 -
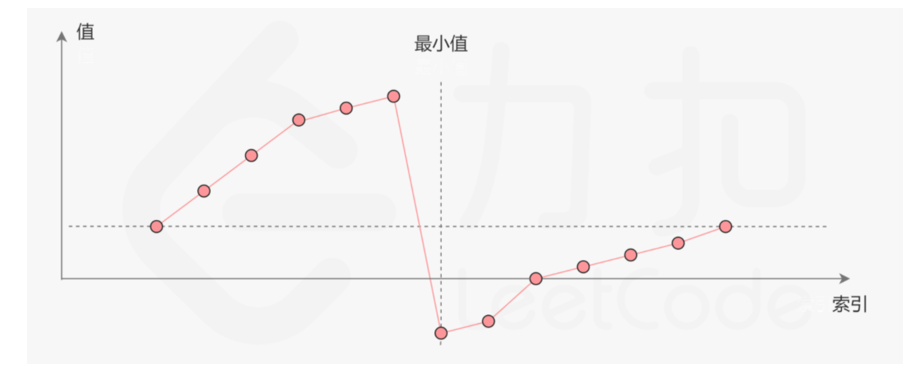
来自LeetCode: 一个不包含重复元素的升序数组在经过旋转之后,可以得到下面可视化的折线图:
-
-
其中**横轴表示数组元素的下标,纵轴表示数组元素的值**。图中标出了最小值的位置,是我们需要查找的目标。
-
我们**考虑数组中的最后一个元素 x**:在最小值右侧的元素(不包括最后一个元素本身),它们的值一定都严格小于 x;而在最小值左侧的元素,它们的值一定都严格大于×。因此,我们可以根据这一条性质,通过二分查找的方法找出最小值。
-
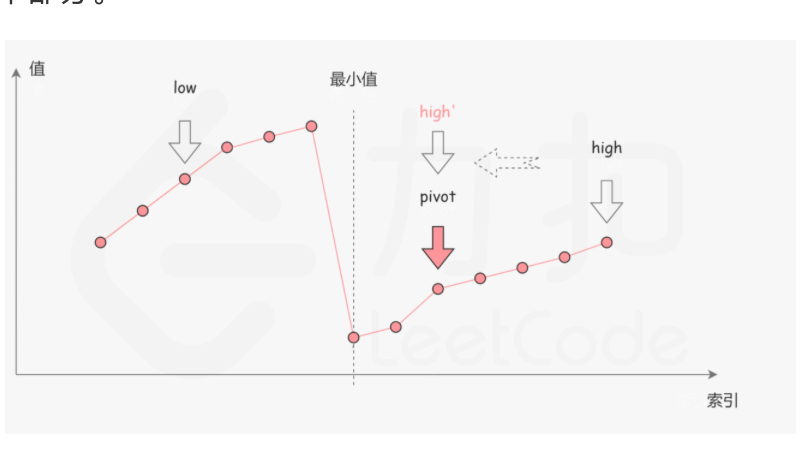
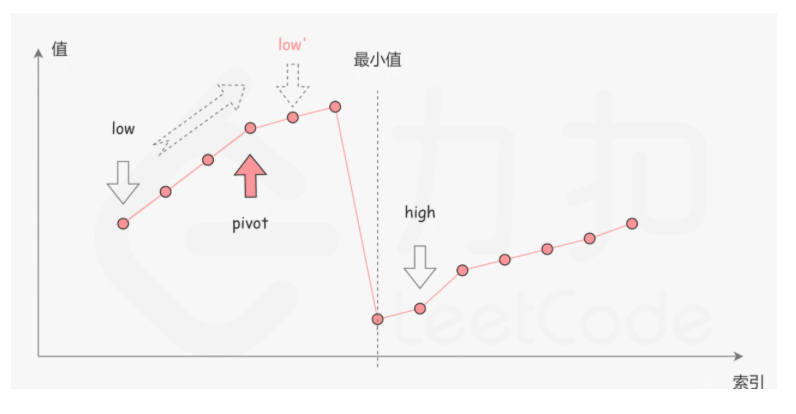
在二分查找的每一步中,左边界为low,右边界为 high,区间的中点为 pivot,最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较,可能会有以下的三种情况:
- 第一种情況是 nums[pivot] < nums[high]。如下图所示,这说明 nums[pivot] 是最小值右侧的元
素,因此我们可以忽略二分查找区间的右半部分。
- 第一种情況是 nums[pivot] < nums[high]。如下图所示,这说明 nums[pivot] 是最小值右侧的元
-
-
第二种情况是 nums[pivot] > nums[high]。如下图所示,这说明numsLpivot」是最小值左侧的元素,因此我们可以忽略二分查找区间的左半部分。
-
-
由于数组不包含重复元素,并且只要当前的区间长度不为1,pivot 就不会与high 重合;而如果当前的区间长度为1,这说明我们已经可以结束二分查找了。因此不会存在 nums[pivot] = nums[high] 的情况。
当二分查找结束时,我们就得到了最小值所在的位置。 -
//时间复杂度是 O(log n) public int findMin(int[] nums){ int low = 0; int high = nums.length-1; //使用二分查找的思想来缩小搜索范围, // 直到 low 和 high 相遇,这时 low 指向的元素就是数组中的最小值。 while(low < high){ int pivot = low + ((high - low) >> 1); if(nums[pivot] < nums[high]){ high = pivot; }else{ low = pivot+1; } } return nums[low]; } -
这里你是否注意到 high = pivot;而不是我们习惯的high = pivot-1呢?这是为了防止遗漏元素,例如 [3,1,2] ,执行的时候 nums[pivot] = 1,小于 nums[high] = 2,此时如果 high= pivot - 1,则直接变成了0。所以对于这种边界情况,很难解释清楚,最好的策略就是多写几种场景测试一下看看。这也是二分查找比较烦的情况,一般来说解释比较困难,也不容易理解清楚,所以写几个典型的例子试一下,面试的时候大部分case能过就能通过。
1.3 找缺失数字
-
剑指offer: 一个长度为 n-1 的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围 0 ~ n-1之内。在范围 0~n-1 内的 n 个数字中有且只有一个数字不在该数组中,请找出这个数字。
-
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8 -
这个题很简单是不?从头到尾遍历一遍即可确定,但是这么简单肯定不是面试需要的。那这个题要考什么呢?就是二分查找。
对于有序的也可以用二分查找,这里的关键点是在缺失的数字之前,必然有 nums[i] == i,在缺失的数字之后,必然有 nums[i] != i。
因此,只需要二分找出第一个 nums[i] = i,此时下标i就是答案。若数组元素中没有找到此下标,那么缺失的就是n。代码如下: -
public int missingNumber(int[] arr){ int left = 0; int right = arr.length; while(left < right){ int mid = left + ((right - left) >> 1); //说明当前索引 mid 的元素是存在的, // 缺失的元素在 mid 的右侧或者就是 mid if(arr[mid] == mid){ left = mid+1; }else{ right = mid-1; } } return left; }
1.4 优化求平方根
-
剑指offer:实现函数 int sqrt(int x).计算并返回x的平方根这个题的思路是用最快的方式找到 n * n = x 的n。如果整数没有平方根,一般采用向下取整的方式得到结果。采用折半进行比较的实现过程是:
-
public int sqrt(int x){ //分别指向搜索范围的下界(1)和上界(即 x 本身) int left = 1, right = x; while(left <= right){ int mid = left + ((right - left) >> 1); if(mid * mid == x){ return mid; }else if(mid * mid > x){ right = mid-1; }else if(mid * mid < x){ left = mid+1; } } return right; } -
这种优化思想要记住,凡是在有序区间查找的场景,都可以用二分查找来优化速度。如果有序区间是变化的,那就每次都针对这个变化的区间进行二分查找。
2 中序与搜索树原理
- 我们发现很多题使用前序、后序或者层次遍历都可以解决,但几乎没有中序遍历的。这是因为中序与前后序相比有不一样的特征,例如中序可以和搜索树结合在一起,但是前后序则不行。
- 二又搜索树是一个很简单的概念,但是想说清楚却不太容易。简单来说就是如果一棵二叉树是搜索树,则**按照中序遍历其序列正好是一个递增序列**。比较规范的定义是:
•若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
•若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
•它的左、右子树也分别为二叉排序树。下面这两棵树一个中序序列是{3,6,9,10,14,16,19},一个是{3,6,9,10},因此都是搜索树: 
- 搜索树的题目虽然也是用递归,但是与前后序有很大区别,主要是因为搜索树是有序的,就可以根据条件决定某些递归就不必执行了,这也称为“剪枝”。
2.1 二叉搜索树中搜索特定值
-
LeetCode 700:给定二叉搜索树(BST)的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在,则返回 NULL。例如:
-

-
本题看起来很复杂,但是实现非常简单,递归:
- 如果根节点为空 root == null 或者根节点的值等于搜索值 val == root.val, 返回根节点。
- 如果 val < root.val,进入根节点的左子树查找 searchBST(root.left, val)。
- 如果 val > root.val,进入根节点的右子树查找 searchBST(root.right, val)。
-
public TreeNode searchBST(TreeNode root, int val){ if(root == null || root.val == val){ return root; } if(val > root.val){ return searchBST(root.right, val); } if(val < root.val){ return searchBST(root.left, val); } return root; } -
如果采用**迭代方式**,也不复杂:
- 如果根节点不空 root != null 且根节点不是目的节点 val != root.val:
- 如果 val < root.val,进入根节点的左子树查找 root = root.left。
- 如果 val > root.val,进入根节点的右子树查找 root = root.right。
-
public TreeNode searchBST(TreeNode root, int val){ while(root != null && root.val != val) { //说明目标值可能在右子树中 if(val > root.val){ root = root.right; } //说明目标值可能在左子树中 if(val < root.val){ root = root.left; } } return root; }
2.2 验证二叉搜索树
-
LeetCode98:给你一个二叉树的根节点 root,判断其是否是一个有效的二又搜索树。
有效 二又搜索树定义如下:- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例:
-
示例1:
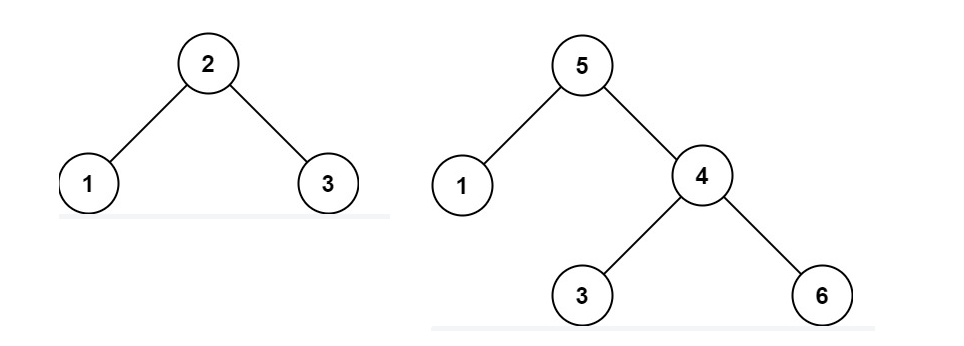
输入:root = [2, 1, 3]
输出:true
示例2:
输入:root = [5, 1, 4, null, null, 3, 6]
输出:false
解释:根节点的值是 5, 但是右子节点的值是 4. -
-
根据题目给出的性质,我们可以进一步知道二又搜索树「中序遍历」得到的值构成的序列一定是升序的,在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。
-
long pre = Long.MIN_VALUE; public boolean isValidBST(TreeNode root){ //空树被认为是有效的二叉搜索树。 if(root == null){ return true; } //如果左子树无效,或者在左子树中已经发现了违反二叉搜索树性质的节点 // (即左子树中的某个节点的值大于或等于当前节点的值), // 则整个树无效,返回 false。 if(!isValidBST(root.left)){ return false; } //访问当前节点:如果当前节点小于等于中序遍历的前一个节点。 //说明不满足BST,返回false if(root.val <= pre){ return false; } pre = root.val; //访问右子树 return isValidBST(root.right); }