数据结构与算法笔记：递归函数设计技巧

news2024/11/15 12:32:46

ACM金牌带你零基础直达C语言精通-课程资料

本笔记属于船说系列课程之一，课程链接：

哔哩哔哩_bilibilihttps://www.bilibili.com/cheese/play/ep66799?csource=private_space_class_null&spm_id_from=333.999.0.0

你也可以选择购买『船说系列课程-年度会员』产品『船票』，畅享一年内无限制学习已上线的所有船说系列课程：船票购买入口https://www.bilibili.com/cheese/pages/packageCourseDetail?productId=598

做题网站OJ：HZOJ - Online Judge

Leetcode :力扣 (LeetCode) 全球极客挚爱的技术成长平台

递归函数

一.数学归纳法:

基础步骤：证明当自然数为某个确定的值时，命题成立。这个基础情况通常是 n = 1 或者 n = 0，有时也可能是其他特定的值。

归纳步骤：假设命题对于一个自然数 k 成立，然后证明在此假设下，命题对于下一个自然数 k+1 也成立。

结合前两步骤，根据归纳法，命题对于所有大于等于基础情况的自然数都成立。

列子比如：

证明： $1 + 3 + ... + (2 * n - 1) = n^{2}$ 前2n项的基数和等于n的平方

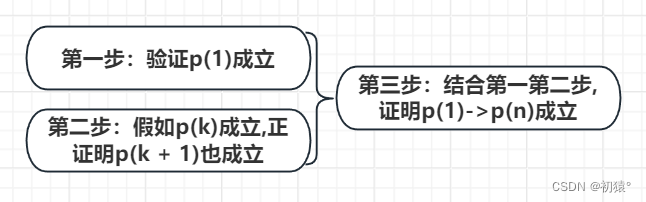
第一步：证明p(1)

p(1) = 1 = $1^{2}$

第二步:假如p(k)成立，证明p(k + 1)成立

p(k + 1) = $p(k) + (2 * k + 1) = k^{2} + 2 * k + 1 = (k + 1)^{2}$

第三步:证明p(1)到p(n)，都成立

由于p(1)正确，又因为前一项成立，那么后一项也成立，那么通过归纳就可以得到p(1)->p(n)都成立

总结：通过学习数学归纳法后，放在程序中去分析对应的情况，这样就可以来判断复杂的代码的正确性，就不用花大量的时间再去测试代码的可行性。

二.递归函数的三个重要部分

1.给递归函数一个明确的语义。

在设计递归函数时，要给明一个对应递归函数的解释，也就是说这个递归函数到底是要用来做什么的，对于这个递归函数设计的目的是什么。

2.实现边界条件时的程序逻辑

对于递归的边界条件就是数学归纳法中第一步的p(1)，因为p(1)是我们可以得到，或者证明得到的结果。所以递归最终递归的最后边界就是p(1)。

3.假设递归函数调用的返回结果是正确的，实现本层函数逻辑。

那这就是数学归纳法的第二步，p(k)成立可以推导出p(k + 1)成立。

带入程序理解：
#include<stdio.h>
//第一点，给递归函数一个明确的语义
//这里的递归函数代表的就是f(n)是求!n
int f(int n) {
    //这里就是递归函数的边界条件
    //也就是p(1),因为!n n = 1时 !n = 1;
    //最终在递归到n = 1时,p(1)成立
    //p(1)成立就可得到，p(2)成立，又反推回去直到f(n)
    if (n == 1) return 1;
    //假设p(k)成立,去证明P(k + 1)也成立,这里就可以理解为p(k + 1) = p(k) * k;
    //那这里就是假设f(n - 1)成立,那么f(n - 1)代表的就是f(n - 1)的阶乘
    return n * f(n - 1);
}

int main() {
    int n;
    scanf("%d", &n);
    printf("!n = %d\n", f(n));
    return 0;
}
在函数这一章中，我讲了一个关于递归函数的例子，可以现在对于递归函数学习后再去看拿到题目：C语言笔记:函数与程序结构-CSDN博客

总结：

对于想要去实现一个递归函数，一定要明确你实现这个递归函数的目的是什么，第二步确定这个递归函数的边界条件是什么，就是证明p(1)，然后把p(1)设置为边界条件，第三步，

去假设p(n - 1)成立，然后用p(n - 1)去得到p(n)，最后通过反推直到证明p(n)。

递归函数理解并不困难，在大量的练习后，慢慢就会熟练的掌握这个过程，再回头来看这个过程起始就非常好理解。