-
在目标检测任务中,样本的划分对于模型的性能具有至关重要的影响。其中,正样本指的是包含目标物体的图像或区域,而负样本则是不包含目标物体的图像或区域。然而,在负样本中,有一部分样本由于其与正样本在特征上的相似性、复杂的背景环境、遮挡或形变等因素,导致模型难以准确区分,这些样本被称为难负样本。难负样本的存在对目标检测模型的性能具有显著影响。由于难负样本与正样本之间的特征差异较小,模型在训练过程中容易将这些样本误判为负样本,从而导致漏检或误检的情况发生。此外,难负样本还可能影响模型的收敛速度和稳定性,使得模型在训练过程中难以达到理想的性能。
- 正样本(Positive Samples):正样本是指那些属于目标类别的样本,它们是我们希望模型能够正确识别并分类的实例。以图像分类任务为例,如果我们正在训练一个识别猫的模型,那么所有包含猫的图像便构成了正样本集。
- 负样本(Negative Samples):负样本则是指不属于目标类别的样本,即模型在训练过程中应将其与正样本区分开来的实例。在上述猫的图像分类任务中,所有不包含猫的图像即构成负样本集。
- 难分正样本(Hard Positives):难分正样本指的是那些在训练过程中被错误地划分为负样本的正样本,或者是在训练过程中产生较高损失的正样本。这些样本对于模型来说较难识别,因此需要更多的关注和优化。
- 难分负样本(Hard Negatives):难分负样本是指那些被错误地划分为正样本的负样本,或者在训练过程中产生较高损失的负样本。这些样本的存在可能导致模型出现误判,因此也是训练过程中需要重点关注的对象。
- 易分正样本(Easy Positives):易分正样本是指那些容易被模型正确分类的正样本,这些样本在训练过程中通常产生较低的损失。它们对于模型的训练来说较为简单,但仍然是构成正样本集的重要部分。
- 易分负样本(Easy Negatives):易分负样本则是指那些容易被模型正确分类的负样本,这些样本在训练过程中同样产生较低的损失。虽然它们对于模型来说较为简单,但在构建完整的训练数据集时,这些样本同样不可忽视。
-
为了处理难负样本问题,研究者们提出了多种方法和技术。首先,难负样本挖掘策略是一种有效的方法。在训练过程中,通过重点关注那些被模型误判的负样本,并增加它们的权重,可以提高模型对这些样本的识别能力。其次,改进损失函数、优化模型结构或使用更强大的特征提取器也是增强模型对难负样本处理能力的重要途径。在选择难负样本时,需要遵循一定的原则。首先,难负样本应与正样本具有不同的标签,以确保模型能够正确区分它们。其次,难负样本应与正样本尽可能相似,以充分挑战模型的识别能力。这两个原则在实际操作中需要找到平衡点,既要保证样本的多样性,又要保证样本的困难度。
-
然而,在利用难负样本进行模型训练时,也需要注意一些实践中的细节。首先,过度依赖难负样本可能导致模型过拟合,因此需要谨慎选择样本并控制其比例。其次,在训练过程中应逐步增加难负样本的比例,以便让模型逐步适应更具挑战性的样本。最后,还需要考虑到计算复杂性和训练效率的问题,避免引入过多的难负样本导致训练过程变得复杂和耗时。为了让模型正常训练,我们必须要通过某种方法抑制大量的简单负例,挖掘所有难例的信息,这就是难例挖掘的初衷。即在训练时,尽量多挖掘些难负例(hard negative)加入负样本集参与模型的训练,这样会比easy negative组成的负样本集效果更好。
-
Fast R-CNN 采用 Selective Search 方法生成约 2k 个候选区域(proposal)作为潜在的物体位置。在训练过程中,这些 proposal 会根据其与真实标注框(ground truth, gt)的交并比(IoU)进行标签分配。具体来说,当 proposal 与 gt 的 IoU 大于等于 0.5 时,该 proposal 被视为正样本;当 IoU 落在 [0.1, 0.5) 区间时,虽然与真实物体有一定的重叠,但不足以被认定为正样本,因此被标记为负样本;而当 IoU 小于 0.1 时,proposal 与真实物体几乎无重叠,这类样本同样被标记为负样本,但它们对于难例挖掘尤为关键。难例挖掘(Hard Negative Mining)是一种专门处理负样本中难以区分样本的技术。在目标检测任务中,由于负样本数量通常远超过正样本,直接训练可能会导致分类器偏向于将样本预测为负类,从而忽视了一些与正样本相似但实际为负的困难样本。这些困难样本对模型的性能提升至关重要,因为它们有助于增强模型对复杂背景、遮挡或形变等因素的识别能力。难例挖掘的核心思想是在保证正负样本比例均衡的前提下,从负样本中筛选出那些最有可能被误判为正样本的困难样本,并将其加入负样本集进行训练。具体操作如下:
- 首先,计算所有负样本在模型训练过程中的损失值。损失值反映了模型对样本的预测准确度,损失值越大,说明模型对该样本的预测越不准确,即该样本越难区分。
- 然后,根据损失值对负样本进行排序,从大到小选择损失值较高的前 K 个样本作为困难负样本。这里,K 通常设置为正样本数量的几倍,以确保正负样本之间的平衡。
- 最后,将这些筛选出的困难负样本与正样本一起用于模型的训练。通过这种方式,模型能够更加关注那些难以区分的样本,从而提高其整体性能。
-
Faster R-CNN 包含两个核心组件:RPN(Region Proposal Network)head 和 R-CNN head。RPN head 负责生成候选区域(proposals),而 R-CNN head 则对这些候选区域进行进一步的分类和回归,以产生更精确的边界框(bounding boxes)。RPN head 的输出包含两部分:分类和回归。分类部分执行二分类任务,旨在区分前景(即潜在的物体)和背景。回归部分则仅针对前景样本(正样本)进行基于 anchor 的变换回归,以调整 anchor 的位置和大小,使其更接近真实的物体边界。R-CNN head 的输出同样包含分类和回归两部分。分类部分的输出是类别数加1(其中1代表背景类),用于预测物体的具体类别。回归部分则仅针对前景样本进行基于 ROI 的变换回归,以产生更精确的边界框。R-CNN head 的目标是对 RPN 提取的 ROI 特征进行精细调整,输出更加准确的边界框。在 Faster R-CNN 中,正负样本的定义是基于 MaxIoUAssigner 的,但 RPN 和 R-CNN 对于正负样本的阈值设置有所不同。正负样本的准确定义对于模型的训练至关重要。MaxIoUAssigner 的操作步骤如下:
- 初始化阶段,将每个 anchor 的 mask 设置为 -1,表示所有 anchor 初始时均被视为忽略区域。
- 计算每个 anchor 与所有真实标注框(ground truth boxes)的最大 IoU 值。如果某个 anchor 的最大 IoU 值小于负样本阈值(neg_iou_thr),则将其 mask 设置为 0,标记为负样本(背景样本)。
- 对于每个 anchor,找到与其 IoU 值最大的 ground truth box。如果该最大 IoU 值大于或等于正样本阈值(pos_iou_thr),则将该 anchor 的 mask 设置为 1,表示该 anchor 负责预测对应的 ground truth box,是一个高质量的 anchor。
- 由于可能存在某些 ground truth box 没有分配到对应的 anchor(因为 IoU 值低于 pos_iou_thr),因此需要进一步处理。对于每个 ground truth box,找到与其 IoU 值最大的 anchor。如果该 IoU 值大于最小正样本 IoU 值(min_pos_iou),则将该 anchor 的 mask 设置为 1,表示该 anchor 负责预测对应的 ground truth box。这一步确保了每个 ground truth box 都有至少一个 anchor 负责预测。如果仍然无法满足 min_pos_iou 的条件,则将该 ground truth box 视为忽略样本。
- 注意,在步骤 3 和步骤 4 中,某些 anchor 可能会被重复分配。例如,当某个 anchor 的最大 IoU 值大于 pos_iou_thr 时,它肯定也会大于 min_pos_iou。此时,这两个步骤都会将该 anchor 标记为正样本。
- 最终,每个 ground truth box 可能与多个 anchor 匹配,但每个 anchor 只能与一个 ground truth box 匹配。未被分配为正样本或负样本的 anchor 将被视为忽略区域,不参与梯度的计算。这种最大分配策略确保了每个 ground truth box 都有合适的高质量 anchor 负责预测。
- 由于 R-CNN head 的输入是 RPN head 输出的 ROI,这些 ROI 与 ground truth box 的 IoU 值通常较高,因此 R-CNN head 面临的是更高质量的样本。因此,在 R-CNN head 中,最小正样本 IoU 值(min_pos_iou)的阈值通常设置得较高。此外,由于 pos_iou_thr 和 neg_iou_thr 在 R-CNN head 中通常也设置为较高的值(如 0.5),因此在实际操作中,忽略区域的情况在 R-CNN head 中较为少见。在 Faster R-CNN 中,存在大量的正负样本不平衡问题。为了解决这个问题,可以采用正负样本采样或调整损失函数等方法。Faster R-CNN 默认采用正负样本采样策略进行平衡。RPN head 和 R-CNN head 的采样器都相对简单,主要基于随机采样,但阈值设置有所不同。此外,为了稳定 R-CNN head 的训练过程,特别是在网络训练的早期阶段,通常会向 R-CNN head 添加一些 ground truth box 作为额外的正样本。在采样过程中,如果正样本或负样本的数量不足,可以全部保留这些样本。需要注意的是,原始的 Faster R-CNN 使用的损失函数是交叉熵损失(CE)和 SmoothL1 损失,这些损失函数本身并不直接解决正负样本不平衡的问题。因此,在实际应用中,可能需要结合其他策略(如调整损失函数的权重)来进一步平衡正负样本的影响。
-
熵是什么?熵存在的意义是啥?为什么叫熵?这是3个非常现实的问题。答案非常明确:在机器学习中熵是表征随机变量分布的混乱程度,分布越混乱,则熵越大,在物理学上表征物质状态的参量之一,也是体系混乱程度的度量;熵存在的意义是度量信息量的多少,人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少,这时熵的意义就体现出来了
-
自信息是熵的基础,理解它对后续理解各种熵非常有用。自信息表示某一事件发生时所带来的信息量的多少,当事件发生的概率越大,则自信息越小,或者可以这样理解:某一事件发生的概率非常小,但是实际上却发生了(观察结果),则此时的自信息非常大;某一事件发生的概率非常大,并且实际上也发生了,则此时的自信息较小。现在要寻找一个函数,它要满足的条件是:事件发生的概率越大,则自信息越小;自信息不能是负值,最小是0;自信息应该满足可加性,并且两个独立事件的自信息应该等于两个事件单独的自信息。下面给出自信息的具体公式:
-
I ( p i ) = − l o g ( p i ) I(p_i)=-log(p_i) I(pi)=−log(pi)
-
其中 p i p_i pi 表示随机变量的第 i 个事件发生的概率,自信息单位是bit,表征描述该信息需要多少位。可以看出,自信息的计算和随机变量本身数值没有关系,只和其概率有关,同时可以很容易发现上述定义满足自信息的3个条件。
-
信息熵通常用来描述整个随机分布所带来的信息量平均值,更具统计特性。信息熵也叫香农熵,在机器学习中,由于熵的计算是依据样本数据而来,故也叫经验熵。其公式定义如下:
-
H ( x ) = − ∑ i = 1 n ( p ( x i ) l o g p ( x i ) ) = − ∫ x p ( x ) l o g p ( x ) d x H(x)=-\sum_{i=1}^n(p(x_i)logp(x_i))=-\int_x p(x)logp(x)dx H(x)=−i=1∑n(p(xi)logp(xi))=−∫xp(x)logp(x)dx
-
从公式可以看出,信息熵H(X)是各项自信息的累加值,由于每一项都是整正数,故而随机变量取值个数越多,状态数也就越多,累加次数就越多,信息熵就越大,混乱程度就越大,纯度越小。越宽广的分布,熵就越大,在同样的定义域内,由于分布宽广性中脉冲分布<高斯分布<均匀分布,故而熵的关系为脉冲分布信息熵<高斯分布信息熵<均匀分布信息熵。熵代表了随机分布的混乱程度,这一特性是所有基于熵的机器学习算法的核心思想。推广到多维随机变量的联合分布,其联合信息熵为:
-
H ( X , Y ) = − ∑ i = 1 n ∑ j = 1 m p ( x i , y j ) l o g ( x i , y j ) H(X,Y)=-\sum_{i=1}^n\sum_{j=1}^mp(x_i,y_j)log(x_i,y_j) H(X,Y)=−i=1∑nj=1∑mp(xi,yj)log(xi,yj)
-
熵只依赖于随机变量的分布,与随机变量取值无关;定义0log0=0(因为可能出现某个取值概率为0的情况);熵越大,随机变量的不确定性就越大,分布越混乱,随机变量状态数越多。
-
条件熵的定义为:在X给定条件下,Y的条件概率分布的熵对X的数学期望。
-
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) = ∑ i = 1 n p ( x ) H ( Y ∣ X = x ) H(Y|X)=H(X,Y)-H(X)=\sum_{i=1}^np(x)H(Y|X=x) H(Y∣X)=H(X,Y)−H(X)=i=1∑np(x)H(Y∣X=x)
-
交叉熵广泛用在逻辑回归的Sigmoid和softmax函数中作为损失函数使用,softmax只是对sigmoid在多分类上面的推广。其主要用于度量两个概率分布间的差异性信息,由于其和相对熵非常相似。p对q的交叉熵表示q分布的自信息对p分布的期望,公式定义为:
-
H ( p , q ) = − ∑ i = 1 n p ( x ) l o g q ( x ) H(p,q)=-\sum_{i=1}^np(x)logq(x) H(p,q)=−i=1∑np(x)logq(x)
-
其中。p是真实样本分布,q是预测得到样本分布。在信息论中,其计算的数值表示:如果用错误的编码方式q去编码真实分布p的事件,需要多少bit数,是一种非常有用的衡量概率分布相似性的数学工具。
-
相对熵的作用和交叉熵差不多。相对熵经常也叫做KL散度,在贝叶斯推理中, D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q) 衡量当你修改了从先验分布 q 到后验分布 p 的之后带来的信息增益*。*首先给出其公式:
-
D K L ( p ∣ ∣ q ) = − ∑ i = 1 n p ( x ) q ( x ) p ( x ) = H ( p , q ) − H ( p ) D_{KL}(p||q)=-\sum_{i=1}^np(x)\frac{q(x)}{p(x)}=H(p,q)-H(p) DKL(p∣∣q)=−i=1∑np(x)p(x)q(x)=H(p,q)−H(p)
-
相对熵较交叉熵有更多的优异性质,主要为:当p分布和q分布相等时候,KL散度值为0,这是一个非常好的性质;非对称的,通过公式可以看出,KL散度是衡量两个分布的不相似性,不相似性越大,则值越大,当完全相同时,取值为0。简单对比交叉熵和相对熵,可以发现仅仅差了一个H§,如果从优化角度来看,p是真实分布,是固定值,最小化KL散度情况下,H§可以省略,此时交叉熵等价于KL散度。
-
最大化似然函数,等价于最小化负对数似然,等价于最小化交叉熵,等价于最小化KL散度。
-
互信息可以评价两个分布之间的距离,这主要归因于其对称性,假设互信息不具备对称性,那么就不能作为距离度量,例如相对熵,由于不满足对称性,故通常说相对熵是评价分布的相似程度,而不会说距离。互信息的定义为:一个随机变量由于已知另一个随机变量而减少的不确定性,或者说从贝叶斯角度考虑,由于新的观测数据 y 到来而导致 x 分布的不确定性下降程度。公式如下:
-
I ( X , Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X , Y ) = H ( X , Y ) − H ( X ∣ Y ) − H ( Y ∣ X ) \begin{aligned}I(X,Y)&=H(X)-H(X|Y)\\ &=H(Y)-H(Y|X)\\ &=H(X)+H(Y)-H(X,Y)\\ &=H(X,Y)-H(X|Y)-H(Y|X) \end{aligned} I(X,Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)=H(X,Y)−H(X∣Y)−H(Y∣X)
-
互信息和相对熵也存在联系,如果说相对熵不能作为距离度量,是因为其非对称性,那么互信息的出现正好弥补了该缺陷,使得我们可以计算任意两个随机变量之间的距离,或者说两个随机变量分布之间的相关性、独立性。互信息也是大于等于0的,当且仅当x与y相互独立时候取等号。
-
-
retinanet的网络结构。主要特点是:(1) 多尺度预测输出;(2) 采用FPN结构进行多层特征图融合。 网络进行多尺度预测,尺度一共是5个,每个尺度共享同一个head结构,但是分类和回归分支是不共享权重的。FocalLoss是本文重点,是用于处理分类分支中大量正负样本不平衡问题,或者说大量难易样本不平衡问题。 作者首先也深入分析了OHEM的不足:它通过对loss排序,选出loss最大的example来进行训练,这样就能保证训练的区域都是hard example,这个方法的缺陷,是把所有的easy example(包括easy positive和easy negitive)都去除掉了,造成easy positive example无法进一步提升训练的精度(表现的可能现象是预测出来了,但是bbox不是特别准确),而且复杂度高影响检测效率。
-
故作者提出一个简单且高效的方法:Focal Loss焦点损失函数,用于替代OHEM,功能是一样的,需要强调的是:FL本质上解决的是将大量易学习样本的loss权重降低,但是不丢弃样本,突出难学习样本的loss权重,但是因为大部分易学习样本都是负样本,所以顺便解决了正负样本不平衡问题。 其是根据交叉熵改进而来,本质是dynamically scaled cross entropy loss,直接按照loss decay掉那些easy example的权重,这样使训练更加bias到更有意义的样本中去,说通俗点就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss。
-
C E ( p t ) = − l o g ( p t ) F L ( p t ) = − ( 1 − p t ) γ l o g ( p t ) CE(p_t)=-log(p_t)\\ FL(p_t)=-(1-p_t)^\gamma log(p_t) CE(pt)=−log(pt)FL(pt)=−(1−pt)γlog(pt)
-
公式表示label必须是one-hot形式。只看图示就很好理解了,对于任何一个类别的样本,本质上是希望学习的概率为1,当预测输出接近1时候,该样本loss权重是很低的,当预测的结果越接近0,该样本loss权重就越高。而且相比于原始的CE,这种差距会进一步拉开。由于大量样本都是属于well-classified examples,故这部分样本的loss全部都需要往下拉。
-
-
FCOS堪称anchor free论文的典范,因为其结构主流,思路简单清晰,效果蛮好,故一直是后续anchor free的基准对比算法。FCOS的核心是将输入图像上的位置作为anchor point的中心点,并且对这些anchor point进行回归。fcos的骨架和neck部分是标准的 resnet+fpn 结构,和retinanet完全相同。FCOS是全卷积预测模式,对于cls分支,输出是h * w * (class+1),每个空间位置值为1,表示该位置有特定类别的 gt bbox,对于回归分支,输出是h * w * 4,其4个值的含义是:
- 每个点回归的4个数代表距离4条边的距离,非常简单易懂。 和所有目标检测算法一样,需要提前定义好正负样本,同时由于是多尺度预测输出,还需要首先考虑 gt 由哪一个输出层具体负责。 作者首先设计了 min_size 和 max_size 来确定某个 gt 到底由哪一层负责,具体设置是 0, 64, 128, 256, 512 和无穷大,也就是说对于第1个输出预测层而言,其stride=8,负责最小尺度的物体,对于第1层上面的任何一个空间位置点,如果有 gt bbox 映射到特征图上,满足0 < max(中心点到4条边的距离) < 64,那么该 gt bbox 就属于第1层负责,其余层也是采用类似原则。总结来说就是第1层负责预测尺度在0~64范围内的gt,第2层负责预测尺度在64~128范围内的gt,其余类推。通过该分配策略就可以将不同大小的 gt 分配到最合适的预测层进行学习。
- 需要确定在每个输出层上面,哪些空间位置是正样本区域,哪些是负样本区域。原版的fcos的正负样本策略非常简单粗暴:在bbox区域内的都是正样本,其余地方都是负样本,而没有忽略样本区域。可想而知这种做法不友好,因为标注本身就存在大量噪声,如果bbox全部区域都作为正样本,那么bbox边沿的位置作为正样本负责预测是难以得到好的效果的,显然是不太靠谱的(在文本检测领域,都会采用 shrink 的做法来得到正样本区域),所以后面又提出了center sampling的做法来确定正负样本,具体是:引入了center_sample_radius(基于当前stride参数)的参数用于确定在半径范围内的样本都属于正样本区域,其余区域作为负样本,依然没有定义忽略样本。默认配置center_sample_radius=1.5,如果第1层为例,其stride=8,那么也就是说在该输出层上,对于任何一个gt,基于gt bbox中心点为起点,在半径为1.5*8=12个像素范围内都属于正样本区域。
- 肯定存在大量正负样本不平衡问题,故作者对于分类分支采用了one-stage常用的focal loss;对于bbox回归问题,由于很多论文表明直接优化bbox比单独优化4个值更靠谱,故作者采用了GIOU loss来回归4个值,对于center-ness分支,采用的是CrossEntropyLoss,当做分类问题处理。
- center-ness作用比较大,从上面的正负样本定义就可以看出来,如果没有center-ness,对于所有正样本区域,其距离bbox中心不同远近的loss权重居然是一样的,这明显是违反直觉的,理论上应该越是远离 Bbox 中心的空间位置,其权重应该越小,作者实验也发现如果没有center-ness分支,会产生大量假正样本,导致很多虚检。center-ness本质就是对正样本区域按照距离gt bbox中心来设置权重。
-
centernet也是非常流行的anchor-free论文,其核心是:一些场景的cv任务例如2d目标检测、3d目标检测、深度估计和关键点估计等等任务都可以建模成以物体中心点学习,外加上在该中心点位置处额外学习一些各自特有属性的通用做法。对于目标检测,可以将bbox回归问题建模成学习bbox中心点+bbox宽高问题。
- centernet的输出也非常简单,其相比较于FCOS等算法,使用更大分辨率的输出特征图(缩放了4倍),本质上是因为其采用关键点检测思路做法,而关键点检测精度要高,通常是需要输出高分辨率特征图,同时不需要多尺度预测。其输出预测头包含3个分支,分别是 分类分支h’ * w’ * (c+1),如果某个特定类的gt bbox的中心点落在某个位置上,那么该通道的对应位置值设置为1,其余为0;offset分支h’ * w’ * 2,用于学习量化偏差,图像下采样时,gt bbox的中心点会因数据是离散的而产生偏差,例如gt bbox的中心点坐标是101,而由于输入和输出相差4倍,导致gt bbox映射到特征图上坐标由25.25量化为了25,这就出现了101-25x4=1个pix的误差,如果下采样越大,那么量化误差会越大,故可以使用offset分支来学习量化误差,这样可以提高预测精度。宽高分支h’ * w’ * 2,表示gt bbox的宽高。
- 由于objects as points的建模方式和FCOS的建模方式不一样,故centernet的正负样本定义就会产生很大区别。主要是宽高分支的通道数是2,而不是4,也就是说其输入到宽高分支的正样本其实会非常少,必须是gt bbox的中心位置才是正样本,左右偏移位置无法作为正样本,也没有啥忽略样本的概念,这个是和FCOS的最大区别。由于centernet特殊的建模方式,故其正负样本定义特别简单,不需要考虑多尺度、不需要考虑忽略区域,也不用考虑iou,正样本定义就是某个gt bbox中心落在哪个位置上,那么那个位置就是正样本,其余位置全部是负样本。
- 对于centernet,其正负样本定义非常简单,可以看出会造成极其严重的正负样本不平衡问题,然后也无法像two-stage算法一样设计正负样本采样策略,那么平衡问题就必须要在loss上面解决。 对于offset和宽高预测分支,其只对正样本位置进行监督,故核心设计就在平衡分类上面。 对于分类平衡loss,首选肯定是focal loss了,但是还不够,focal loss的核心是压制大量易学习样本的权重,但是由于我们没有设置忽略区域,在正样本附近的样本,实际上非常靠近正样本,如果强行设置为0背景来学习,那其实相当于难负样本,focal loss会突出学这部分区域,导致loss难以下降、不稳定,同时也是没有必要的,因为我们的label虽然是0或者1的,但是在前向后处理时候是当做高斯热图(0~1之间呈现2d高斯分布特点)来处理的,我们学到最后的输出只要满足gt bbox中心值比附近区域大就行,不一定要学习出0或者1的图。
- 基于上述设定,在不修改分类分支label的情况下,在使用focal loss的情况下,作者的做法是对正样本附近增加惩罚,基于2d高斯分布来降低这部分权重,相当于起到了类似于忽略区域的作用。可以简单认为是focal focal loss。
- 宽高和offset的监督仅仅在gt bbox中心位置,其余位置全部是忽略区域。这种做法其实很不鲁棒,也就是说bbox性能其实完全靠分类分支,如果分类分支学习的关键点有偏差,那么由于宽高的特殊监督特性,可能会导致由于中心点定位不准而带来宽高不准的情况(特别的如果中心点预测丢失了,那么宽高预测再准也没有用)
-
anchor-free和anchor-base算法的本质区别是啥?性能为啥不一样?最终结论是其本质区别就在于正负样本定义不同。只要我们能够统一正负样本定义方式,那么anchor-free和anchor-base就没有啥实际区别了,性能也是非常一致的。要想彻底理解不同目标检测算法的区别,那么对于正负样本定义必须要非常清楚。从point回归就是指的每个点预测距离4条边的距离模式,而从anchor回归是指的retinanet那种基于anchor回归的模式。
-
retinanet和fcos的正负样本定义策略的不同,首先这两个算法都是多尺度预测的,故其实都包括两个步骤:gt分配给哪一层负责预测;gt分配给哪一个位置anchor负责预测。retinanet完全依靠统一的iou来决定哪一层哪一个位置anchor负责预测,而fcos显式的分为两步:先利用scale ratio来确定gt分配到哪一层,然后利用center sampling策略来确定哪些位置是正样本。RetinaNet在特征图上每个点铺设多个anchor,而FCOS在特征图上每个点只铺设一个中心点,这是数量上的差异。RetinaNet基于anchor和GT之间的IoU和设定的阈值来确定正负样本,而FCOS通过GT中心点和铺设点之间的距离和尺寸来确定正负样本。
-
RetinaNet通过回归矩形框的2个角点偏置进行预测框位置和大小的预测,而FCOS是基于中心点预测四条边和中心点的距离进行预测框位置和大小的预测。这1点可以从下图的对比中看到,蓝色框和点表示GT,红色框表示RetinaNet的正样本,红色点表示FCOS的正样本。首先将RetinaNet在每个点铺设的anchor数量减少到1,也就是和FCOS保持一致。
-

-
对于retinanet算法,正负样本定义采用iou阈值,回归分支采用原始的anchor变换回归模式(box),mAP=37.0,采用fcos的point模式是36.9,说明到底是point还是box不是关键因素。但是如果换成fcos的正负样本定义模式,mAP就可以上升为37.8,和fcos一致了,说明正负样本定义的不同是决定anchor-base和anchor-free的本质区别。fcos的正负样本定义策略比retinanet好,但是fcos算法需要定义超参scale constraint,比较麻烦,作者希望找到一种和fcos类似功能的正负样本定义算法,主要特定是几乎没有超参,或者说对超参不敏感,可以自适应,故作者提出ATSS算法。
- 对于每个输出的检测层,选计算每个anchor的中心点和目标的中心点的L2距离,选取K(9)个anchor中心点离目标中心点最近的anchor为候选正样本(candidate positive samples)
- 计算每个候选正样本和groundtruth之间的IOU,计算这组IOU的均值和方差根据方差和均值,设置选取正样本的阈值:t=m+g ;m为均值,g为方差。均值(所有层的候选样本算出一个均值)代表了anchor对gt衡量的普遍合适度,其值越高,代表候选样本质量普遍越高,iou也就越大,而方差代表哪一层适合预测该gt bbox,方差越高越能区分层和层之间的anchor质量差异。均值和方差相加就能够很好的反应出哪一层的哪些anchor适合作为正样本。一个好的anchor设计,应该是满足高均值、高方差的设定。
- 根据每一层的t从其候选正样本中选出真正需要加入训练的正样本
-
-
Soft Anchor-Point Object Detection算法首先针对当前anchor-free方法的两大问题——attention bias和feature selection——提出了创新的soft策略。其核心在于对正负样本定义策略的精细化调整。该算法遵循anchor point类算法的基本框架,即每个点学习其到四条边界的距离,这与densebox算法流程相似,但与FCOS算法有所区别。主要差异体现在:1)未采用center-ness分支;2)正样本区域的定义采用了四条边界向内收缩的方法,而非center sampling。
- Attention bias关注的是特定输出层内正负样本的界定问题,而feature selection则着眼于不同输出层间正负样本的划分。传统的正负样本定义方式往往是hard的,而本文提出的解决策略是soft的。对于特定输出层内的soft正负样本定义,作者通过引入类似于center-ness的权重,实现了对损失函数的优化。对于不同输出层间的soft正负样本定义,作者则采用了网络自动学习soft权重的方法。
- 在输出层内的hard正负样本定义上,作者仍采用了与FCOS相似的策略,但正样本区域是通过边界向内收缩得到的,而非center sampling。在输出层间的hard正负样本定义上,作者摒弃了FCOS的分配策略,提出了创新的soft代替hard的方法。本文不再预先设定某一输出层负责特定gt bbox的回归,而是允许每一层都参与所有gt bbox的回归,并通过网络自主学习金字塔层级的权重。
- 为了学习金字塔权重,作者设计了一个简单的网络。该网络利用gt bbox映射到对应的特征图层,通过roialign层提取特征,并使用一个简单的分类器输出每个层级的权重。由于金字塔层数为5,因此全连接层的输出维度也为5。在label设置上,作者借鉴了FSAF(Feature Selective Anchor-Free Module for Single-Shot Object Detection)的思想,即不再人为指定哪一层负责预测GT,而是根据loss最小的原则动态选择最合适的层。本文的meta选择网络并非预先计算独热码label,而是根据输出softmax层的值或loss来动态选择。具体来说,哪个输出节点的loss最小,则将其label设置为1,其余为0。整个meta选择网络与目标检测网络联合训练。
- 对于特定输出层内的soft正负样本定义问题,作者通过引入类似于center-ness的权重来解决。这种权重设计对距离gt bbox中心点进行惩罚,中心点的权重最大,往外依次减少。这种设计与centernet中的权重设置有所不同。在centernet中,focal loss的权重设置在半径范围内,离中心点越近,权重越小,往外依次增加;而本文的设计则是离中心点越近,权重越大,往外依次减少。这种差异源于label设计规则的不同。在centernet中,除了中心点是正样本外,其余均为负样本;而本文中,不仅中心点是正样本,收缩区域附近的点也被视为正样本。因此,本文的权重设置规则与centernet相反。通过这种设计,特定层内的正负样本定义由原先的hard变为了soft;而在层级间,原先的正负样本定义是硬性的,即只分配到特定层,其余层均为0,现在则引入了soft操作,权重由网络自主学习得到。
-
Guided Anchoring,anchor-base的做法都需要预设anchor,特别是对于one-stage而言,anchor设置的好坏对结果影响很大,因为anchor本身不会改变,所有的预测值都是基于anchor进行回归,一旦anchor设置不太好,那么效果肯定影响很大。而对于two-stage而言,好歹还有一个rcnn层,其可以对RPN的输出roi(动态anchor)进行回归,看起来影响稍微小一点。 不管是one stage还是two-stage,不管咋预测,肯定都是基于语义信息来预测的,在bbox内部的区域激活值肯定较大,这种语义信息正好可以指导anchor的生成,也就是本文的出发点:通过图像特征来指导 anchor 的生成。通过预测 anchor 的位置和形状,来生成稀疏而且形状任意的 anchor。 可以发现此时的anchor就是动态的了。 如果将faster rcnn进行改造,将RPN层替换为ga层,那肯定也是可以的,如果将retinanet或者yolo的预测层替换为ga,那其实就完全变成了anchor-free了。但是作者采用了一种更加优雅的实现方式,其采用了一种可以直接插入当前anchor-base网络中进行anchor动态调整的做法,而不是替换掉原始网络结构,属于锦上添花,从此anchor-base就变成了anchor-base混合anchor-free了(取长补短),这就是一个不错的进步。
- 以retinanet为例,但是可以应用于所有anchor-base论文中。 核心操作就是在预测xywh的同时,新增两条预测分支,一条分支是loc(batch,anchor_num * 1,h,w),用于区分前后景,目标是预测哪些区域应该作为中心点来生成 anchor,是二分类问题,这个非常好理解,另一条分支是shape(batch,anchor_num * 2, h,w),用于预测anchor的形状。 一旦训练好了,那么应该anchor会和语义特征紧密联系。
- 对于任何一层,都会输出4条分支,分别是anchor的loc_preds,anchor的shape_preds,原始retinanet分支的cls_scores和bbox_preds。
- 使用阈值将loc_preds预测值切分出前景区域,然后提取前景区域的shape_preds,然后结合特征图位置,concat得到4维的guided_anchors(x,y,w,h)
- 此时的guided_anchors就相当于retinanet里面的固定anchor了,然后和原始retinanet流程完全相同,基于guided_anchors和cls_scores、bbox_preds分支就可以得到最终的bbox预测值了。
- anchor的定位模块就是个二分类问题,希望学习出前景区域。这个分支的设定和大部分anchor-free的做法是一样的(例如fcos)。首先对每个gt,利用FPN中提到的roi重映射规则,将gt映射到不同的特征图层上,定义中心区域和忽略区域比例,将gt落在中心区域的位置认为是正样本,忽略区域是忽略样本(模糊样本),其余区域是背景负样本,这种设定规则很常用;采用focal loss进行训练
- loc_shape分支的目标是给定 anchor 中心点,预测最佳的长和宽,这是一个回归问题。首先预测宽高,那肯定是回归问题,采用 l1 或者 smooth l1 就行了,关键是label是啥?还有哪些位置计算Loss?我们知道retinanet计算bbox 分支的target算法就是利用MaxIoUAssigner来确定特征图的哪些位置anchor是正样本,然后将这些anchor进行bbox回归。现在要预测anchor的宽高,当然也要确定这个问题。
- 第一个问题:如何确定特征图的哪些位置是正样本区域?,注意作者采用的anchor个数其实是1(作者觉得既然是动态anchor,那么个数其实影响不会很大,设置为1是可以的错),也就是说问题被简化了,只要确定每个特征图的每个位置是否是正样本即可。要解决这个问题其实非常容易,做法非常多,完全可以按照anchor-free的做法即可,例如FOCS,其实就是loc_preds分支如何确定正负样本的做法即可,确定中心区域和忽略区域。将中心区域的特征位置作为正样本,然后直接优化预测输出的anchor shape和对应gt的iou即可。但是论文没有这么做,我觉得直接按照fcos的做法来确定正样本区域,然后回归shape,是完全可行。本文做法是采用了ApproxMaxIoUAssigner来确定的,ApproxMaxIoUAssigner和MaxIoUAssigner非常相似,仅仅多了一个Approx,其核心思想是:利用原始retinanet的每个位置9个anchor设定,计算9个anchor和gt的iou,然后在9个anchor中采用max操作,选出每个位置9个iou中最高的iou值,然后利用该iou值计算后续的MaxIoUAssigner,此时就可以得到每个特征图位置上哪些位置是正样本了。简单来说,ApproxMaxIoUAssigner和MaxIoUAssigner的区别就仅仅是ApproxMaxIoUAssigner多了一个将9个anchor对应的iou中取最大iou的操作而已。对于第二个问题:正样本位置对应的shape target是啥,其实得到了每个位置匹配的gt,那么对应的target肯定就是Gt值了。
-
FPN操作是一个非常常用的用于对付大小尺寸物体检测的办法,作者指出FPN的缺点是不同尺度之间存在语义gap,举例来说基于iou准则,某个gt bbox只会分配到某一个特定层,而其余层级对应区域会认为是背景(但是其余层学习出来的语义特征其实也是连续相似的,并不是完全不能用的),如果图像中包含大小对象,则不同级别的特征之间的冲突往往会占据要素金字塔的主要部分,这种不一致会干扰训练期间的梯度计算,并降低特征金字塔的有效性。一句话就是:目前这种concat或者add的融合方式不够科学。本文觉得应该自适应融合,自动找出最合适的融合特征。
- 简要思想就是:原来的FPN add方式现在变成了add基础上多了一个可学习系数,该参数是自动学习的,可以实现自适应融合效果,类似于全连接参数。 ASFF具体操作包括 identically rescaling和adaptively fusing。 定义FPN层级为 l,为了进行融合,对于不同层级的特征都要进行上采样或者下采样操作,用于得到同等空间大小的特征图,上采样操作是1x1卷积进行通道压缩,然后双线性插值得到;下采样操作是对于1/2特征图是采样3 × 3 convolution layer with a stride of 2,对于1/4特征图是add a 2-stride max pooling layer然后引用stride 卷积。
- 首先对于第 l 级特征图输出c * h * w,对其余特征图进行上下采样操作,得到同样大小和channel的特征图,方便后续融合
- 对处理后的3个层级特征图输出,输入到1*1*n的卷积中(n是预先设定的),得到3个空间权重向量,每个大小是n*h*w。
- 然后通道方向拼接得到3n*h*w的权重融合图,为了得到通道为3的权重图,对上述特征图采用1*1*3的卷积,得到3*h*w的权重向量。在通道方向softmax操作,进行归一化,将3个向量乘加到3个特征图上面,得到融合后的c*h*w特征图。
-
由于GA论文(Region proposal by guided anchoring)指出采用语义向导式的anchor策略可以得到更好的结果,故作者也引入了GA操作来提升性能。 可以看出,结合这些策略后,在coco上面可以得到38.8的mAP,速度仅仅慢了一点点(多了GA操作),可谓是非常强大,这也反应出训练策略对最终性能的影响非常大。在anchor设置不合理时候,动态引导anchor预测分支得到更好的anchor,在anchor设置合理时候,可以加速收敛,且可以进一步refine 默认anchor
目标检测标签分配策略,难样本挖掘策略
news2026/2/9 0:41:34
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1574401.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
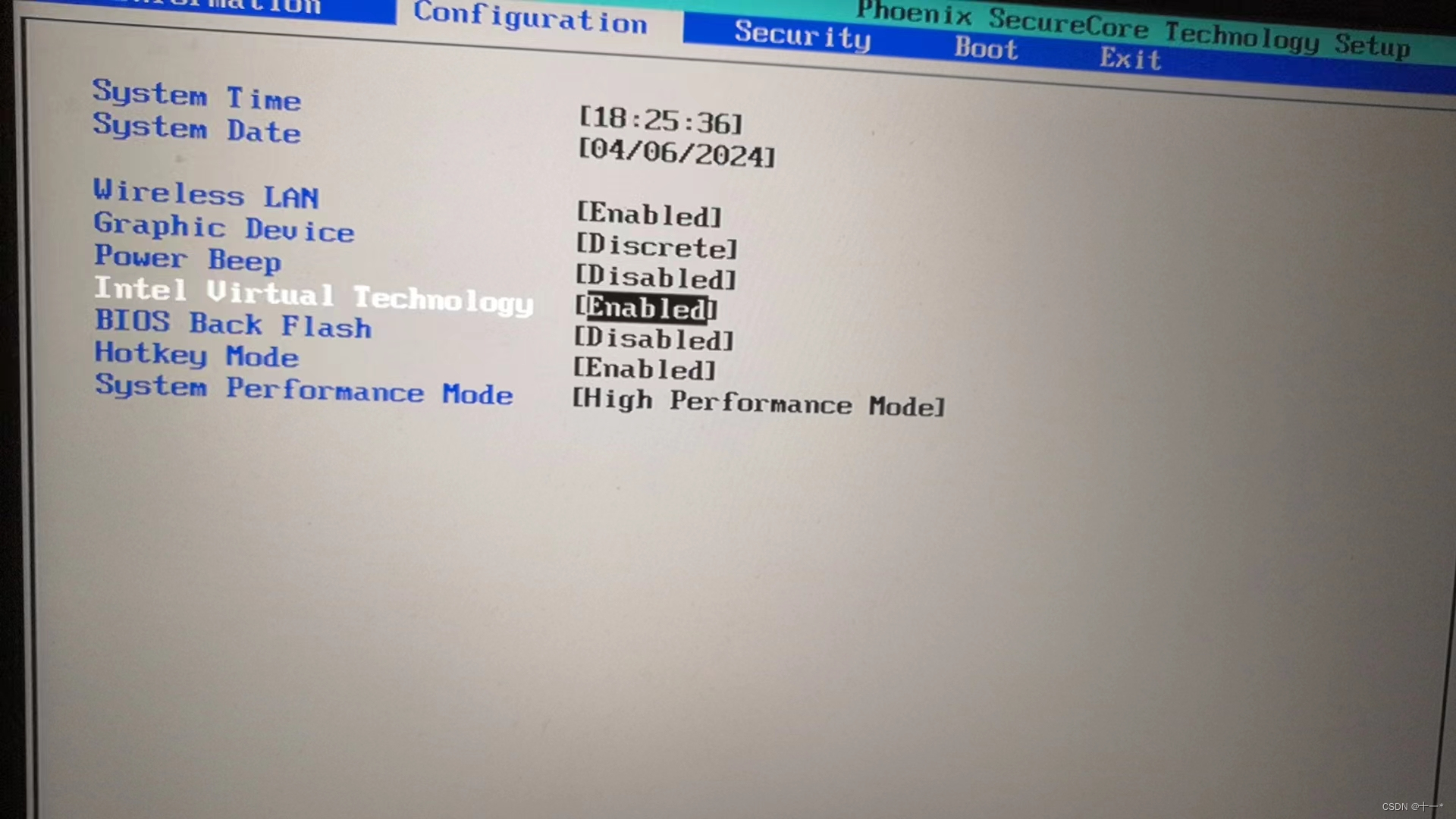
开启虚拟机时出现此主机支持 Intel VT-x,但 Intel VT-x 处于禁用状态怎么解决
问题描述
虚拟机安装完成后,点击开启此虚拟机弹出系统提示
原因分析:
Intel VT-x 处于禁用状态,需要开启。 解决方案:
以联系小新笔记本电脑为例,进入BIOS界面,将Intel Virtual Technology设置成Enabl…
在不同操作系统中搭建Python编程环境
1 在不同操作系统中搭建Python编程环境
1.1 在Linux系统中搭建Python编程环境
1. 检查Python版本
在你的系统中运行应用程序Terminal(如果你使用的是Ubuntu,可按Ctrl Alt T),打开一个终端窗口。为确定是否安装了Python&…
SpringBoot实现邮箱验证
目录
1、开启邮箱IMAP/SMTP服务,获取授权码
2、相关代码 1、使用配置Redis(用于存储验证码,具有时效性) 2、邮箱依赖和hutool(用于随机生成验证码) 3、配置Redis和邮箱信息 4、开启Redis服务 5、编写发送…
广东智慧公厕管理系统哪家好@光明源
随着城市发展和人民生活水平的提高,智慧公厕作为城市公共卫生设施的重要组成部分,受到了越来越多城市管理者的重视。在广东,智慧公厕管理系统的选择成为了一个备受关注的话题。那么,在广东,到底哪家智慧公厕管理系统比…
某程旅行安全工程师一面
一、自我介绍
阿吧阿吧,不多说了
二、两段实习经历,看你在南京中孚数据安全部做实习生,你能大概讲一下做什么的吗
当时做的是一个隐写溯源项目,是我们实验室跟南京中孚那边共同合作的。主要是针对电子文档信息泄露,…
牛市来临,模块化赛道可能会出现下个以太坊?
市场专家普遍预测,2024年将成为加密货币市场迎来新一轮牛市的关键时刻。研究人员将下一次比特币(BTC)减半以及2024年现货BTC ETF(交易所交易基金)的可能性视为推动下一次牛市的潜在因素。这一牛市的可能爆发有望吸引大…
C# Web应用调用EXE文件的一些实践
目录
需求
范例运行环境
可执行文件的设计
调用可执行文件方法
RunExecuteFile
RunShellExecuteFile
方法的区别
WEB调用举例
小结 需求
最近同事使用Python开发了一款智能文字转语音的程序,经讨论部署在WINDOWS环境服务器下,因此需要生成目标…
C语言函数实现冒泡排序
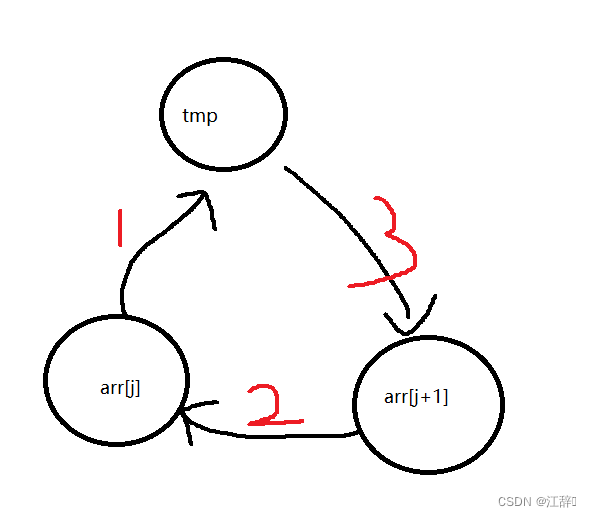
前言 今天我们来看看怎么使用函数的方式实现冒泡排序吧,我们以一个数组为例arr[] {9,8,7,6,5,4,3,2,1,0},我们将这个数组通过冒泡排序的方式让他变为升序吧。 代码实现 #include<stdio.h>
void bubble_sort(int arr[], int sz)
{int i 0;for (i 0;i < s…
如何使用GraphQL和Apollo构建一个宝可梦应用
宝可梦是一个由视频游戏、动画系列与电影、交换卡牌游戏以及其他相关媒体组成的日本媒体特许经营权。
在本文中,我们将使用一个宝可梦GraphQL API,该API提供有关不同宝可梦的数据。
我们将使用Apollo和GraphQL来处理数据获取,以及React来构…
数据库之DCL操作(用户、访问权限。)
DCL英文全称是Data control language(数据控制语言),用来管理数据库用户、控制数据库的访问权限。
1.管理用户
1.1查询用户
select * from mysql.user; 其中 Host代表当前用户访问的主机,如果为localhost,仅代表只能够在当前本机访问&…
git上传到本地仓库
摘要:本地初始化init仓库,进行pull和push;好处是便于利用存储设备进行git备份 git init --bare test.git 随便到一个空的目录下git clone 然后使用git上传 把git仓库删除之后再clone一次验证一下是否上传成功: 如果在ubantu上面没…
嵌入式面向对象学习 RT-Thread I/O 设备管理框架 设备驱动层 案例测试
嵌入式面向对象 RT-Thread I/O 设备管理框架 设备驱动层
注:本文介绍性内容转载于《RT-Thread记录(十、全面认识 RT-Thread I/O 设备模型)》
注: 本次使用的开发板 :
兆易创新GD32F407VET6开发板
雅特力科技…
c++的学习之路:7、类和对象(3)
目录 一、初始化列表
二、static成员
三、友元
四、内部类
五、匿名对象
六、类和对象的思维导图 一、初始化列表
初始化列表:以一个冒号开始,接着是一个以逗号分隔的数据成员列表,每个"成员变量"后面跟一个放在括号中的初始…
求m和n的最大公约数(C语言)
一、运行结果; 二、源代码;
# define _CRT_SECURE_NO_WARNINGS
# include <stdio.h>int main()
{//初始化变量值;int remainder 1;int m 0;int n 0;int middle 0;//提示用户;printf("请输入整数m和n的值ÿ…
撸代码时,有哪些习惯一定要坚持?
我从2011年开始做单片机开发,一直保持以下撸代码的习惯。 1.做好代码版本管理
有些人,喜欢一个程序干到底,直到实现全部的产品功能,我以前做51单片机的项目就是这样。 如果功能比较多的产品,我不建议这样做࿰…
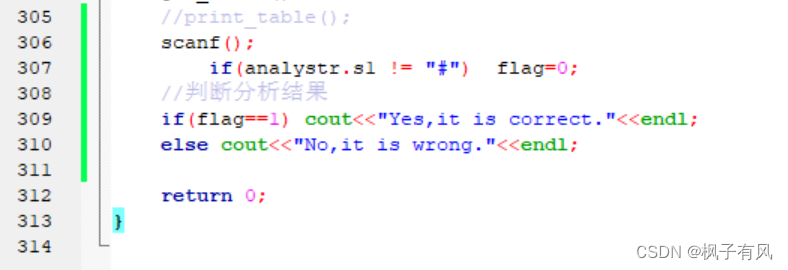
编译原理实验2(自上而下语法分析)
一、实验目的
给出 PL/0 文法规范,要求编写 PL/0 语言的语法分析程序。通过设计、编制、调试一个典型的自上而下语法分析程序,实现对词法分析程序所提供的单词序列进行语法检查和结构分析,进一步掌握常用的语法分析方法。选择有代表性的语法…
一款轻量、干净的 Vue 后台管理框架
开始之前
在开始介绍之前我想谈谈为什么要自己做一个后台管理,我知道很多人都用一些开源的后台管理项目,这些老前辈有很多亮点值得学习,但是存在的一些问题同样不可忽视,我认为很多开发者会被困扰(仅代表个人观点) 技术栈老旧不升…
面试(03)————多线程和线程池
一、多线程
1、什么是线程?线程和进程的区别?
2、创建线程有几种方式 ?
3、Runnable 和 Callable 的区别?
4、如何启动一个新线程、调用 start 和 run 方法的区别?
5、线程有哪几种状态以及各种状态之间的转换?
6、线程…
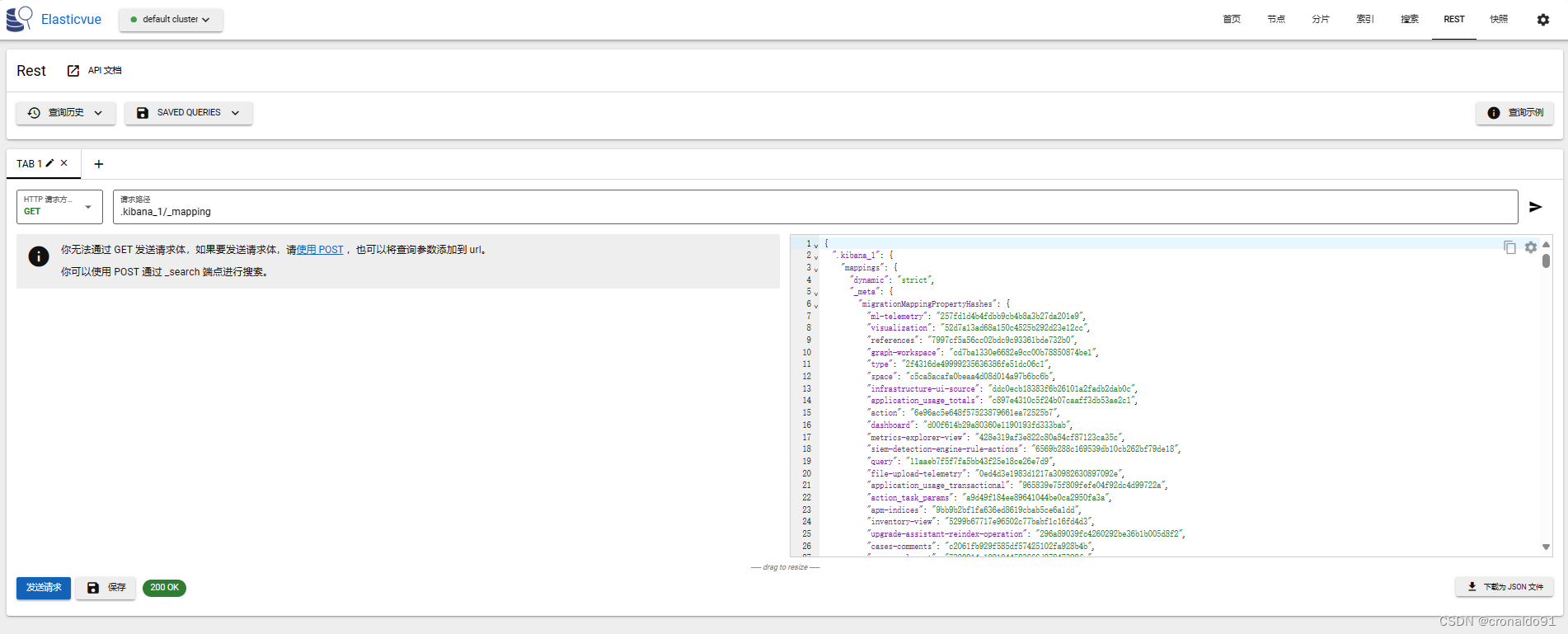
Docker容器与虚拟化技术:OpenEuler 部署 ES 与 Kibana
目录
一、实验
1.环境
2.OpenEuler 部署 ES (EalasticSearch)
3.OpenEuler 部署 Kibana
4.部署 Elasticvue插件
5.使用cpolar内网穿透
6.使用Elasticvue 一、实验
1.环境
(1)主机
表1 主机
系统架构版本IP备注LinuxopenEuler22.03 LTS SP2 1…