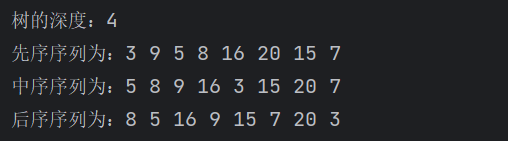
二叉树的结点用一个数组顺序存储，-1表示该节点为空，实现求该二叉树的深度、先序遍历、中序遍历、后序遍历

首先定义一个 Node 类 ，用于表示二叉树中的节点。

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

 创建二叉树

def create_binary_tree(a, index):    #a是顺序存储树节点的数组
    if index >= len(a) or a[index] == -1:    #如果下标超过或者本来该结点为空 
        return None
    node = Node(a[index])
    node.left = create_binary_tree(a, 2 * index + 1)    #创建node结点的左子树 
    node.right = create_binary_tree(a, 2 * index + 2)    #创建node结点的右子树
    # 数组下标从0开始，所以2i+1是左孩子，2i+2是右孩子    
    return node

dfs算法求树的深度

def dfs(root, res, max_depth):    #res是当前深度， max_depth是最大深度
    if root is None:    #递归结束条件
        return max_depth
    if root.left is None and root.right is None:    #如果是叶子结点
        if res > max_depth:    #判断当前深度是否大于最大深度
            max_depth = res    #如果是就更新最大深度
    max_depth = dfs(root.left, res + 1, max_depth)    #递归左子树
    max_depth = dfs(root.right, res + 1, max_depth)    #递归右子树
    return max_depth

 先序遍历函数

def pre_order(root):    #根左右
    if root is None:
        return
    print(root.val, end=" ")
    pre_order(root.left)
    pre_order(root.right)

中序遍历函数

def in_order(root):    #左根右
    if root is None:
        return
    in_order(root.left)
    print(root.val, end=" ")
    in_order(root.right)

 后序遍历函数

def post_order(root):    #左右根
    if root is None:
        return
    post_order(root.left)
    post_order(root.right)
    print(root.val, end=" ")

 主函数

if __name__ == "__main__":
    arr = [3, 9, 20, 5, 16, 15, 7, -1, 8]
    tree = create_binary_tree(arr, 0)
    #创建二叉树tree，该树实质是一个结点，该结点直接或间接指向其它结点 
    depth = dfs(tree, 1, 0)
    print("树的深度：",end="")
    print(depth)

    print("先序序列为：", end="")
    pre_order(tree)
    print()

    print("中序序列为：", end="")
    in_order(tree)
    print()

    print("后序序列为：", end="")
    post_order(tree)

 

运行结果