目录
- 1.概述
- 2.代码实现
- 3.应用
1.概述
(1)广度优先遍历 (Breadth First Search),又称宽度优先遍历,是最简便的图的搜索算法之一。
(2)已知图 G = (V, E) 和一个源顶点 start,宽度优先搜索以一种系统的方式探寻 G 的边,从而“发现” start 所能到达的所有顶点,并计算 start 到所有这些顶点的距离(最少边数),该算法同时能生成一棵根为 start 且包括所有可达顶点的广度优先树。对从 start 可达的任意顶点 v,广度优先树中从 start 到 v 的路径对应于图 G 中从 start 到 v 的最短路径,即包含最小边数的路径。该算法对有向图和无向图同样适用。
(3)之所以称之为广度优先遍历,是因为算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展,就是说,算法首先搜索和 start 距离为 k 的所有顶点,然后再去搜索和 start 距离为 k + 1 的其他顶点。
2.代码实现
(1)当使用邻接矩阵来表示图时,其代码实现如下:
class Solution {
/*
adjMatrix 为邻接矩阵,adjMatrix[i][j] = 0 表示节点 i 和 j 之间没有边直接相连
start 为遍历的起点
*/
public void bfs(int[][] adjMatrix, int start) {
// n 表示图中的节点数量,节点编号为 0 ~ n - 1
int n = adjMatrix.length;
//定义 visited 数组,防止对节点进行重复遍历
boolean[] visited = new boolean[n];
Queue<Integer> queue = new LinkedList<>();
if (start < 0 || start > n - 1) {
System.out.println("起点编号应为 [0, " + (n - 1) + "] 之间的整数!");
return;
}
//起点入队
queue.offer(start);
//标记起点
visited[start] = true;
System.out.print(start + " ");
while (!queue.isEmpty()) {
int node = queue.poll();
//将与节点 node 相连的节点加入到 queue 中
for (int i = 0; i < n; i++) {
if (adjMatrix[node][i] != 0 && !visited[i]) {
System.out.print(i + " ");
visited[i] = true;
queue.offer(i);
}
}
}
}
}
(2)当使用邻接表来表示图时,其代码实现如下:
class Solution {
/*
adjList 为邻接表,adjList[i] 中存储与节点 i 相邻的节点
start 为遍历的起点
*/
public void bfs(List<Integer>[] adjList, int start) {
// n 表示图中的节点数量,节点编号为 0 ~ n - 1
int n = adjList.length;
//定义 visited 数组,防止对节点进行重复遍历
boolean[] visited = new boolean[n];
Queue<Integer> queue = new LinkedList<>();
if (start < 0 || start > n - 1) {
System.out.println("起点编号应为 [0, " + (n - 1) + "] 之间的整数!");
return;
}
//起点入队
queue.offer(start);
//标记起点
visited[start] = true;
System.out.print(start + " ");
while (!queue.isEmpty()) {
int node = queue.poll();
//将与节点 node 相连的节点加入到 queue 中
for (int nextNode : adjList[node]) {
while (!visited[nextNode]) {
System.out.print(nextNode + " ");
visited[nextNode] = true;
queue.offer(nextNode);
}
}
}
}
}
(3)下面以图 G 为例来说明:
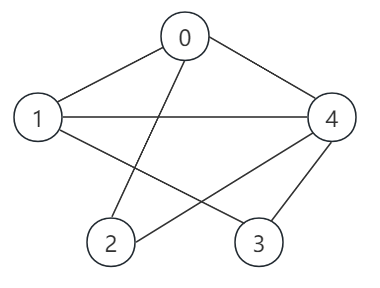
① 构造邻接矩阵:
int[][] adjMatrix = {
{0, 1, 1, 0, 1},
{1, 0, 0, 1, 1},
{1, 0, 0, 0, 1},
{0, 1, 0, 0, 1},
{1, 1, 1, 1, 0}
};
② 构造邻接表:
int n = 5;
List<Integer>[] adjList = new ArrayList[n];
for (int i = 0; i < n; i++) {
adjList[i] = new ArrayList<>();
}
adjList[0].add(1);
adjList[0].add(2);
adjList[0].add(4);
adjList[1].add(0);
adjList[1].add(3);
adjList[1].add(4);
adjList[2].add(0);
adjList[2].add(4);
adjList[3].add(1);
adjList[3].add(4);
adjList[4].add(0);
adjList[4].add(1);
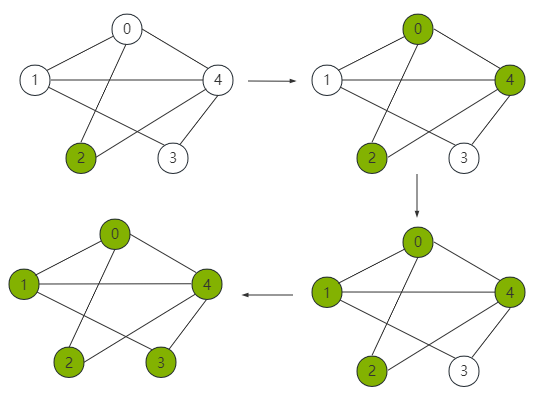
如果 start = 2,那么遍历的节点依次为:
2 0 4 1 3
遍历过程如下图所示:
(4)无论是邻接表还是邻接矩阵的存储方式,BFS 算法都需要借助一个辅助队列 queue,n 个顶点均需入队一次,在最坏的情况下,空间复杂度为 O(|V|),而时间复杂度与图的存储方式有关:
- 采用邻接矩阵存储方式时,查找每个顶点的邻接点所需的时间为O(|V|),故算法总的时间复杂度为 O(|V|2);
- 采用邻接表存储方式时,每个顶点均需搜索一次(或入队一次),故时间复杂度为 O(|V|),在搜索任一顶点的邻接点时,每条边至少访问一次,故时间复杂度为 O(|E|),算法总的时间复杂度为 O(|V| + |E|);
3.应用
(1)除了对图进行遍历以外,BFS 在求解最短路径或者最短步数上有很多的应用。
(2)LeetCode 中的934.最短的桥这题便是对 BFS 的应用:
思路如下:
① 通过遍历找到数组 grid 中的 1 后进行广度优先搜索,此时可以得到第一座岛的位置集合,记为 island,并将其位置全部标记为 −1。
② 从 island 中的所有位置开始进行 BFS,当它们到达了任意的 1 时,即表示搜索到了第二个岛,搜索的层数就是答案。
代码实现如下:
class Solution {
public int shortestBridge(int[][] grid) {
int n = grid.length;
// dirs 记录遍历的四个方向
int[][] dirs = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
List<int[]> island = new ArrayList<>();
Queue<int[]> queue = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
queue.offer(new int[]{i, j});
grid[i][j] = -1;
while (!queue.isEmpty()) {
int[] land = queue.poll();
int x = land[0];
int y = land[1];
island.add(land);
for (int k = 0; k < 4; k++) {
int nextX = x + dirs[k][0];
int nextY = y + dirs[k][1];
if (nextX >= 0 && nextY >= 0 && nextX < n && nextY < n && grid[nextX][nextY] == 1) {
queue.offer(new int[]{nextX, nextY});
//标记 (nextX, nextY),表示已经访问过该点
grid[nextX][nextY] = -1;
}
}
}
/*
(1) 此时已经找到了题目中描述的两座岛中的一座,并且组成岛的每块陆地的坐标位置都保存在 island 中。
(2) 从 island 中的所有坐标位置开始进行 BFS,当它们达到了任意的 1 时,即表示搜索到了第二座岛,
此时搜索的层数即为答案,在下面的代码中使用 step 来记录。
*/
for (int[] land : island) {
queue.offer(land);
}
int step = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int k = 0; k < size; k++) {
int[] land = queue.poll();
int x = land[0];
int y = land[1];
for (int d = 0; d < 4; d++) {
int nextX = x + dirs[d][0];
int nextY = y + dirs[d][1];
if (nextX >= 0 && nextY >= 0 && nextX < n && nextY < n) {
if (grid[nextX][nextY] == 0) {
queue.offer(new int[]{nextX, nextY});
//标记 (nextX, nextY),表示已经访问过该点
grid[nextX][nextY] = -1;
} else if (grid[nextX][nextY] == 1) {
return step;
}
}
}
}
step++;
}
}
}
}
return 0;
}
}
(3)大家可以去 LeetCode 上找相关的 BFS 的题目来练习,或者也可以直接查看LeetCode算法刷题目录(Java)这篇文章中的 BFS 章节。如果大家发现文章中的错误之处,可在评论区中指出。