文章目录
- 面试经典150题【141-150】
- 208.实现前缀树（Trie树）
- 211. 添加与搜索单词-数据结构设计
- 212.单词搜索II
- 200.岛屿数量
- 130.被围绕的区域
- 133.克隆图
- 399.除法求值（未做）
- 拓扑排序
- 207.课程表
- 210.课程表II
面试经典150题【141-150】
208.实现前缀树（Trie树）
对于sea,sells,she的Trie树
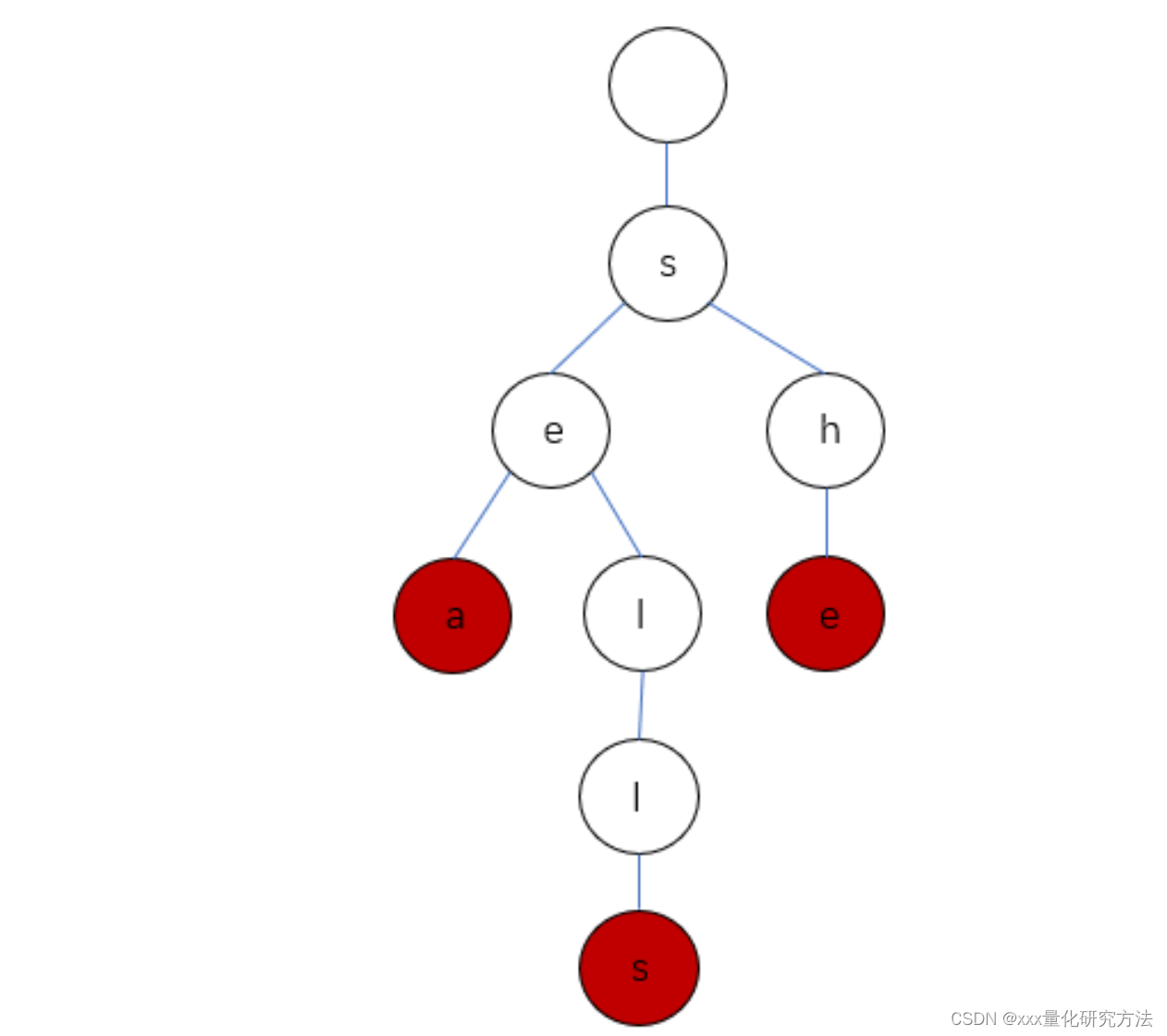
当然其真实是这样的
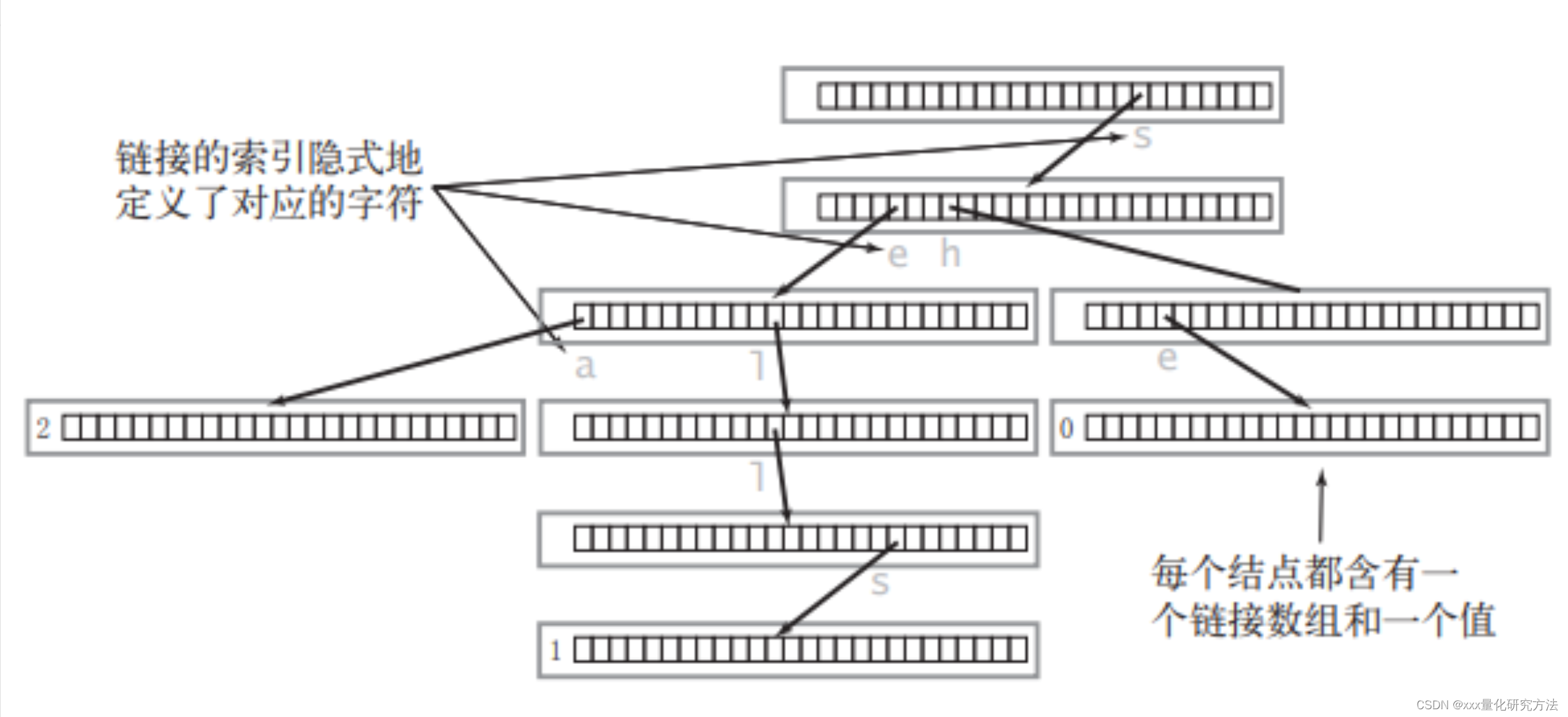首先一个多叉树里面应该有两个属性，是否结尾，下面的元素。
添加的时候，如果没有，就新增一个TrieNode就行。
判断是否存在这个单词，要看最后一位的isEnd。
class Trie {
class TireNode {
private boolean isEnd;
TireNode[] next;
public TireNode() {
isEnd = false;
next = new TireNode[26];
}
}
private TireNode root;
public Trie() {
root = new TireNode();
}
public void insert(String word) {
TireNode node = root;
for (char c : word.toCharArray()) {
if (node.next[c - 'a'] == null) {
node.next[c - 'a'] = new TireNode();
}
node = node.next[c - 'a'];
}
node.isEnd = true;
}
public boolean search(String word) {
TireNode node = root;
for (char c : word.toCharArray()) {
node = node.next[c - 'a'];
if (node == null) {
return false;
}
}
return node.isEnd;
}
public boolean startsWith(String prefix) {
TireNode node = root;
for (char c : prefix.toCharArray()) {
node = node.next[c - 'a'];
if (node == null) {
return false;
}
}
return true;
}
}
211. 添加与搜索单词-数据结构设计
在上一题的基础上，对于搜索部分加了一个DFS
class WordDictionary {
class TireNode {
private boolean isEnd;
public TireNode[] next;
public TireNode() {
isEnd = false;
next = new TireNode[26];
}
}
private TireNode root;
public WordDictionary() {
root = new TireNode();
}
public void addWord(String word) {
TireNode node = root;
for (char c : word.toCharArray()) {
if (node.next[c - 'a'] == null) {
node.next[c - 'a'] = new TireNode();
}
node = node.next[c - 'a'];
}
node.isEnd = true;
}
public boolean search(String word) {
return search(root, word, 0);
}
public boolean search(TireNode root, String word, int start) {
int n = word.length();
if (n == start)
return root.isEnd;
char c = word.charAt(start);
if (c != '.') {
TireNode temp = root.next[c - 'a'];
return temp != null && search(temp, word, start + 1);
}
for (int j = 0; j < 26; j++) {
if (root.next[j] != null && search(root.next[j], word, start + 1))
return true;
}
return false;
}
}
212.单词搜索II
剪枝：我们可以使用 Trie结构进行建树，对于任意一个当前位置 (i,j)而言，只有在 Trie 中存在往从字符 a 到 b 的边时，我们才在棋盘上搜索从 a 到 b 的相邻路径。
需要将平时Trie中的isEnd属性变为String ，这样方便DFS的搜索
public class LC212 {
class TireNode{
String s;
TireNode[] next;
public TireNode() {
next = new TireNode[26];
}
}
Set<String> set = new HashSet<>();
char[][] board;
int n, m;
TireNode root = new TireNode();
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
boolean[][] vis = new boolean[15][15];
void insert(String s){
TireNode p=root;
for(int i=0;i<s.length();i++){
int u=s.charAt(i)-'a';
if(p.next[u]==null) p.next[u]= new TireNode();
p=p.next[u];
}
p.s=s;
}
public List<String> findWords(char[][] _board, String[] words) {
board = _board;
m = board.length; n = board[0].length;
for (String w : words) insert(w);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int u = board[i][j] - 'a';
if (root.next[u] != null) {
vis[i][j] = true;
dfs(i, j, root.next[u]);
vis[i][j] = false;
}
}
}
List<String>ans=new ArrayList<>();
for(String s:set)ans.add(s);
return ans;
}
public void dfs(int i,int j,TireNode node){
if(node.s!=null) set.add(node.s);
for(int[]d:dirs){
int dx=i+d[0],dy=j+d[1];
if(dx<0||dy<0||dx>(m-1)||dy>(n-1)) continue;
if(vis[dx][dy]) continue;
int u=board[dx][dy]-'a';
if (node.next[u] != null) {
vis[dx][dy] = true;
dfs(dx, dy, node.next[u]);
vis[dx][dy] = false;
}
}
}
}
200.岛屿数量
用DFS，BFS，并查集应该都可以做。
DFS：
class Solution {
public void dfs(char[][]grid,int r,int c) {
int len1=grid.length;
int len2=grid[0].length;
grid[r][c]='0';
if(r>0 && grid[r-1][c]=='1') dfs(grid, r-1, c);
if(r<len1-1 && grid[r+1][c]=='1') dfs(grid, r+1, c);
if(c>0 && grid[r][c-1]=='1') dfs(grid, r, c-1);
if(c<len2-1 &&grid[r][c+1]=='1') dfs(grid, r, c+1);
}
public int numIslands(char[][] grid) {
if(grid==null || grid.length==0) return 0;
int ans=0;
for(int i=0;i<grid.length;i++) {
for(int j=0;j<grid[0].length;j++) {
if(grid[i][j]=='1') {
ans++;
dfs(grid, i, j);
}
}
}
return ans;
}
}
当然对于DFS，更通用的模版是先访问，不管是否能访问。
class Solution {
public void dfs(char[][]grid,int r,int c) {
int len1=grid.length;
int len2=grid[0].length;
if(r<0 || r>len1-1 || c<0 || c>len2-1 || grid[r][c]=='0') return;
grid[r][c]='0';
dfs(grid, r-1, c);
dfs(grid, r+1, c);
dfs(grid, r, c-1);
dfs(grid, r, c+1);
}
public int numIslands(char[][] grid) {
if(grid==null || grid.length==0) return 0;
int ans=0;
for(int i=0;i<grid.length;i++) {
for(int j=0;j<grid[0].length;j++) {
if(grid[i][j]=='1') {
ans++;
dfs(grid, i, j);
}
}
}
return ans;
}
}
BFS:
太简单，不写了。
并查集：
class Solution {
class UnionFind {
int count;
int[] parent;
int[] rank;
public UnionFind(char[][] grid) {
count = 0;
int m = grid.length;
int n = grid[0].length;
parent = new int[m * n];
rank = new int[m * n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
parent[i * n + j] = i * n + j;
++count;
}
rank[i * n + j] = 0;
}
}
}
public int find(int i) {
if (parent[i] != i) parent[i] = find(parent[i]);
return parent[i];
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
} else {
parent[rooty] = rootx;
rank[rootx] += 1;
}
--count;
}
}
public int getCount() {
return count;
}
}
public int numIslands(char[][] grid) {
if(grid==null || grid.length==0) return 0;
int nc=grid[0].length;
UnionFind uf=new UnionFind(grid);
for(int i=0;i<grid.length;i++) {
for(int j=0;j<grid[0].length;j++) {
if(grid[i][j]=='1') {
grid[i][j]='0';
if(i>0 && grid[i-1][j]=='1') uf.union(i*nc+j,(i-1)*nc+j);
if(j>0 && grid[i][j-1]=='1') uf.union(i*nc+j,i*nc+j-1);
if(i< grid.length-1 && grid[i+1][j]=='1') uf.union(i*nc+j,(i+1)*nc+j);
if(j< grid[0].length-1 && grid[i][j+1]=='1') uf.union(i*nc+j,i*nc+j+1);
}
}
}
return uf.getCount();
}
}
130.被围绕的区域
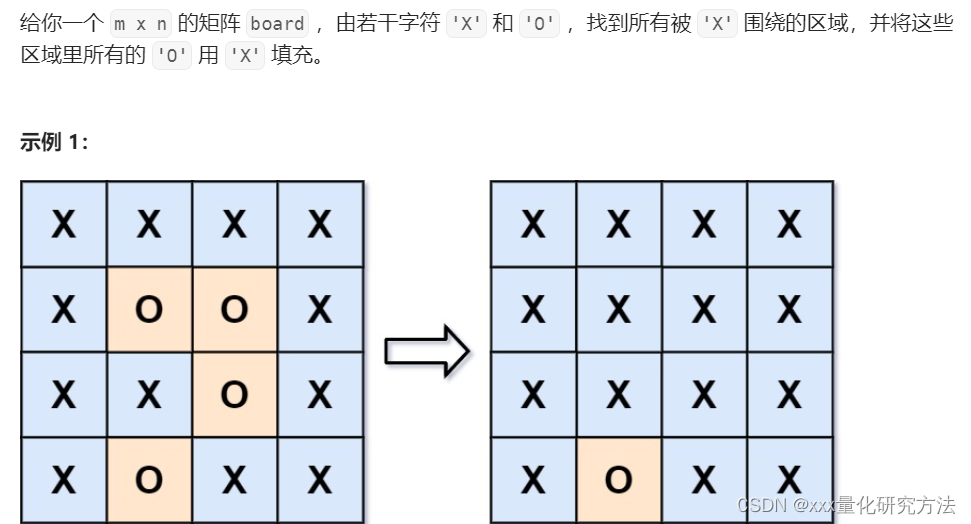
对所有的边缘O进行dfs遍历，将其变为#.再将所有的内陆的O变为X，再将#变为O即可。
class Solution {
public void solve(char[][] board) {
int len1=board.length;
int len2=board[0].length;
for(int i=0;i<len1;i++){
for(int j=0;j<len2;j++){
boolean isEdge = i==0 || i==len1-1 || j==0 || j==len2-1;
if(isEdge && board[i][j]=='O'){
dfs(board,i,j);
}
}
}
for(int i=0;i<len1;i++){
for(int j=0;j<len2;j++){
if(board[i][j]=='O') board[i][j]='X';
if(board[i][j]=='#') board[i][j]='O';
}
}
}
public void dfs(char[][] board,int a,int b){
if(a<0 || b<0 || a> board.length-1 ||b>board[0].length-1 || board[a][b]!='O') return;
if(board[a][b]=='O') board[a][b]='#';
dfs(board,a,b+1);
dfs(board,a,b-1);
dfs(board,a-1,b);
dfs(board,a+1,b);
}
}
133.克隆图
太呆了这题感觉
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
private HashMap<Node, Node> visited = new HashMap<>();
public Node cloneGraph(Node node) {
if (node == null) {
return node;
}
// 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回
if (visited.containsKey(node)) {
return visited.get(node);
}
// 克隆节点，注意到为了深拷贝我们不会克隆它的邻居的列表
Node cloneNode = new Node(node.val, new ArrayList());
// 哈希表存储
visited.put(node, cloneNode);
// 遍历该节点的邻居并更新克隆节点的邻居列表
for (Node neighbor : node.neighbors) {
cloneNode.neighbors.add(cloneGraph(neighbor));
}
return cloneNode;
}
}
399.除法求值（未做）
class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
int nvars = 0;
Map<String, Integer> variables = new HashMap<String, Integer>();
int n = equations.size();
for (int i = 0; i < n; i++) {
if (!variables.containsKey(equations.get(i).get(0))) {
variables.put(equations.get(i).get(0), nvars++);
}
if (!variables.containsKey(equations.get(i).get(1))) {
variables.put(equations.get(i).get(1), nvars++);
}
}
int[] f = new int[nvars];
double[] w = new double[nvars];
Arrays.fill(w, 1.0);
for (int i = 0; i < nvars; i++) {
f[i] = i;
}
for (int i = 0; i < n; i++) {
int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
merge(f, w, va, vb, values[i]);
}
int queriesCount = queries.size();
double[] ret = new double[queriesCount];
for (int i = 0; i < queriesCount; i++) {
List<String> query = queries.get(i);
double result = -1.0;
if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
int fa = findf(f, w, ia), fb = findf(f, w, ib);
if (fa == fb) {
result = w[ia] / w[ib];
}
}
ret[i] = result;
}
return ret;
}
public void merge(int[] f, double[] w, int x, int y, double val) {
int fx = findf(f, w, x);
int fy = findf(f, w, y);
f[fx] = fy;
w[fx] = val * w[y] / w[x];
}
public int findf(int[] f, double[] w, int x) {
if (f[x] != x) {
int father = findf(f, w, f[x]);
w[x] = w[x] * w[f[x]];
f[x] = father;
}
return f[x];
}
}
少有的带权并查集
拓扑排序
最广泛的是用BFS去得到每一个入度为0的，直到最后。
如果只是判断能否成功，则DFS判断是否成环也可以。
207.课程表
注释很详尽
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
//一个可以执行的选课序列
List<Integer>ans=new ArrayList<>();
//每个元素的入度
int[] indegrees = new int[numCourses];
//邻接表
List<List<Integer>> adjacency = new ArrayList<>();
//BFS的队列
Queue<Integer> queue = new LinkedList<>();
//每一个元素在邻接表中都有一行
for(int i=0;i<numCourses;i++){
adjacency.add(new ArrayList<>());
}
//将邻接表和入度填充
for(int[]cp:prerequisites){
indegrees[cp[0]]++;
adjacency.get(cp[1]).add(cp[0]);
}
//找到所有入度为0的课程
for(int i=0;i<numCourses;i++){
if(indegrees[i]==0) queue.add(i);
}
while(!queue.isEmpty()){
int pre=queue.poll();
ans.add(pre);
for(int cur:adjacency.get(pre)){
indegrees[cur]--;
if(indegrees[cur]==0) queue.add(cur);
}
}
return ans.size()==numCourses;
}
}
210.课程表II
题目与上面的一样，只是要输出一个具体的选课列表。代码一模一样，最后转一下就行。
if(ans.size()==numCourses){
return ans.stream().mapToInt(Integer::valueOf).toArray();
}
return new int[0];
