二叉树的顺序存储通过堆已经介绍过了，现在介绍二叉树的链式存储。关于二叉树，有 如下接口：遍历二叉树、计算二叉树的高度、某一层结点的个数、二叉树的结点数等。为了方便验证接口的正确性，这里创建了一个简单的二叉树。

定义二叉树结点的结构体

typedef char BTDataType;
typedef struct BTreeNode
{
	BTDataType val;
	struct BTreeNode* left;
	struct BTreeNode* right;
}BTNode;

创建树的代码如下，该代码只是为了验证接口而写的，并不是真正的创建树的方式，后续会介绍创建树的正确方式。

BTNode* buyNode(BTDataType x)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		return NULL;
	}
	newNode->val = x;
	newNode->left = NULL;
	newNode->right = NULL;

	return newNode;
	
}

BTNode* createTree()
{
	BTNode* n1 = buyNode('A');
	BTNode* n2 = buyNode('B');
	BTNode* n3 = buyNode('C');
	BTNode* n4 = buyNode('D');
	BTNode* n5 = buyNode('E');
	BTNode* n6 = buyNode('F');

	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;
	n4->right = n6;

	return n1;
}

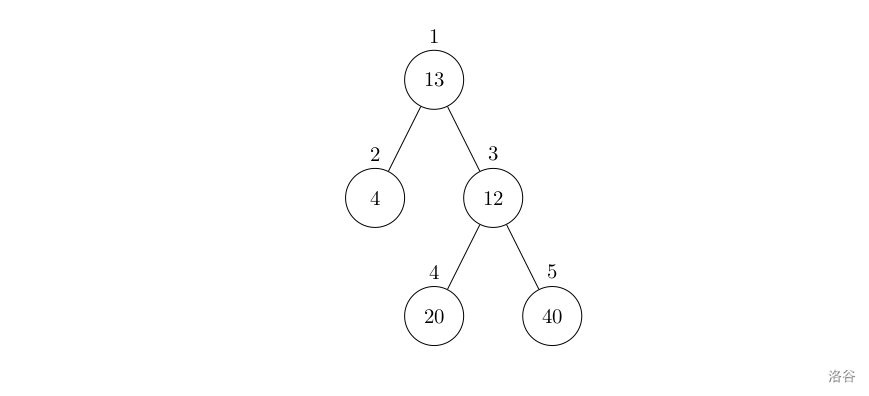
二叉树结构如下图

1. 二叉树的遍历

前序、中序和后序遍历是通过根节点的访问位置来分辨的。
前序：先访问根节点，然后访问左子树和右子树。
中序：先访问左子树，然后访问根节点，再访问右子树。
后序：先访问左子树和右子树，最后访问根节点。
以上三种遍历方式，左右子树也需要按照对应顺序。
此外，介绍的这三种遍历方式都是通过递归实现的
层序：从二叉树的根节点开始，自上而下，从左到右逐层访问每一个结点。

1.1 前序遍历

上图二叉树的前序遍历为：ABDFEC

按照红色，绿色，蓝色的顺序看

代码如下

//前序遍历
void FrontOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%c ", root->val);
	FrontOrder(root->left);
	FrontOrder(root->right);
}

递归需要注意两点：1、分割的子问题 2、最小子问题（返回条件）
在遍历二叉树的例子中，子问题为对每一棵树都分为根和左右子树。最小子问题为该树为空树。

这里画递归图帮助大家理解

右子树类似，因此没有画全。按照函数调用顺序进行打印结果为：ABDFEC

1.2 中序遍历

上图遍历结果为：DFBEAC

和前序类似，只是换了根的访问顺序，就不赘述了。
代码如下

//中序遍历
void MidOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	MidOrder(root->left);
	printf("%c ", root->val);
	MidOrder(root->right);
}

1.3 后序遍历

同理后序也是如此，直接上代码

//后序遍历
void AfterOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	AfterOrder(root->left);
	AfterOrder(root->right);
	printf("%c ", root->val);
}

对于上面三种遍历方式，测试代码和运行结果如图

1.4 层序遍历

层序遍历，需要用到先进先出的队列来辅助实现。

思路大致如下：入队根结点（根节点如果不为空），在进行出队操作，进行出队时，要先把队头结点的左右孩子结点入队。孩子结点为空时，不用入队。当队列为空时，二叉树的层序遍历结束。

过程如下图。

代码如下，用到的关于队列的接口在之前已经介绍过如何实现了，现在只需要将文件复制进项目即可。

添加过程如图

最后在项目中，将.c文件拖动到源文件目录下即可。

// 层序遍历
void TreeLevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
    //创建和初始化队列
	Queue TreeQ;
	QueueInit(&TreeQ);
	//插入根节点
	QueuePush(&TreeQ, root);
	while (!QueueEmpty(&TreeQ))
	{
		//获得队头
		BTNode* front= QueueFront(&TreeQ);

		//将队头结点的左右孩子结点入队
		if(front->left != NULL)
		QueuePush(&TreeQ, front->left);
		if (front->right != NULL)
		QueuePush(&TreeQ, front->right);
		//打印队头结点数值
		printf("%c ", front->val);
		//删除队头
		QueuePop(&TreeQ);
	}
}

测试运行结果如图

2. 二叉树的高度

计算树的高度，子问题为计算左右子树的高度，保留值较大的那一个。最小的子问题为计算空树高度，其高度为0。叶子结点高度为1。

代码如下

//树的高度
int TreeHeight(BTNode* root)
{
    //空树
	if (root == NULL)
	{
		return 0;
	}
	//叶子结点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
    //递归左子树，计算左子树高度
	int left = TreeHeight(root->left);
	//递归右子树，计算右子树高度
	int right = TreeHeight(root->right);
    //返回较高的值，加1是因为需要包括本层高度
	return left > right ? left + 1 : right + 1;
}

力扣里也有此题，链接：计算二叉树的深度

题解代码如下

int calculateDepth(struct TreeNode* root) 
{
    if(root==NULL)
    {
        return 0;
    }
    if(root->left==NULL&&root->right==NULL)
    {
        return 1;
    }
    //这两句不能去掉，去掉后会导致调用函数计算出来的高度不会被保存起来
    //只会知道是左树高度大还是右树高度大，会导致频繁调用函数，最终运行超时
    int leftDepth=calculateDepth(root->left);
    int rightDepth=calculateDepth(root->right);

    return leftDepth>rightDepth?leftDepth+1:rightDepth+1;
}

把上面两句删除，在提交代码，删除前后的结果如下图。

删除前

删除后

当测试用例的二叉树足够大时，会使函数调用次数太多，最终运行超时。

3. 某一层结点的个数

计算任意一层结点的个数，层数小于等于高度。

代码如下

//第k层结点个数
int TreeKsize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeKsize(root->left, k - 1) + TreeKsize(root->right, k - 1);
}

这里通过递归展开图帮助大家理解

假如A没有右子树，那么TreeKsize(root->right, k - 1) 会返回0，因为root->right==NULL。

4. 计算二叉树的结点

有了上面的理解，计算二叉树全部的结点可以转化为计算左右子树的结点数再加1（要包括自己）。最小子问题为空树，结点数为0

代码如下

//树的结点个数
int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return TreeSize(root->left) 
		 + TreeSize(root->right) + 1;
}

5. 叶子结点的个数

同样可以转化为计算左右子树的叶子结点数。最小子问题为空树，返回0。当结点为叶子结点（左右子树都为NULL）时，返回1。

代码如下

// 叶子节点个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

6. 销毁二叉树

销毁二叉树时，不能从根节点开始销毁，销毁根节点后，会导致左右子树找不到。这里选择使用后序遍历的方式来销毁二叉树，先销毁左右子树再销毁根节点。

由于形参和实参都是一个指针，想要通过形参来修改实参的内容，需要传二级指针，因此代码是这样实现的。

// 销毁二叉树
void TreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	TreeDestory(&(*root)->left);
	TreeDestory(&(*root)->right);
	free(*root);
	*root = NULL;
}

对于上面接口的正确性进行验证，运行结果如下图

这里主要是用递归进行解决，递归的代码容易写，但是不太好理解，需要进行适当练习。

关于链式二叉树，就介绍到这里了，剩下的接口会通过OJ题来介绍。也会写一部分的OJ题，练练手。