广度优先和深度优先做这个题 

题目描述

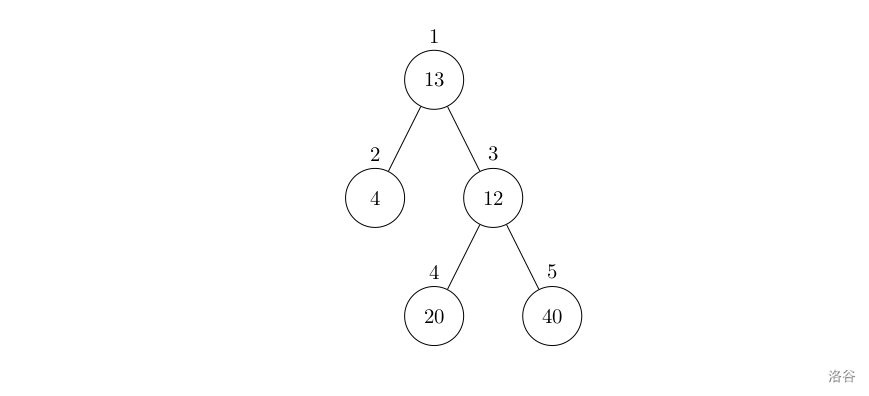
设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 1。如上图中，若医院建在 1 处，则距离和 =4+12+2×20+2×40=136；若医院建在 3 处，则距离和 =4×2+13+20+40=81。

输入格式

第一行一个整数 n，表示树的结点数。

接下来的 n 行每行描述了一个结点的状况，包含三个整数 w,u,v，其中 w 为居民人口数，u 为左链接（为 0 表示无链接），v 为右链接（为 0 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

说明/提示

数据规模与约定

对于 100% 的数据，保证 1≤n≤100，0≤u,v≤n，1≤w≤10^5。

 深度优先

#include<bits/stdc++.h>
using namespace std;
struct node{
	int w,lfte,right,fa;
}q[110];
int sg[110]={0},ant=10000000,sum=0;
void dfs(int t,int x){
	sum+=t*q[x].w;//将所走过的路径权值加起来 
	int L=q[x].lfte,R=q[x].right,F=q[x].fa;
	if(F!=0&&sg[F]==0){//如果当前节点的父节点有值，并且没有走过，则向这个方向搜索，左右判断也一样。当所有节点都被标记走过了，就退出搜索 
		sg[F]=1;
		dfs(t+1,F);
	}
	if(L!=0&&sg[L]==0){
		sg[L]=1;
		dfs(t+1,L);
	}
	if(R!=0&&sg[R]==0){
		sg[R]=1;
		dfs(t+1,R);
	}
	return;
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>q[i].w>>q[i].lfte>>q[i].right; 
		q[q[i].lfte].fa=i;//当前位置的左右孩子的父节点就是当前位置 
		q[q[i].right].fa=i;
	}
	for(int i=1;i<=n;i++){
		memset(sg,0,sizeof(sg));//初始化标记数组 
		sum=0;
		sg[i]=1;
		dfs(0,i);
		ant=min(ant,sum);
	}
	cout<<ant;
	return 0;
}

广度优先

#include<bits/stdc++.h>
using namespace std;
struct node{
	int w,lfte,right,fa,stp;
}q[110];
int sg[110]={0},ant=10000000,sum=0;
void dfs(int x){
    queue<node>q1;
    q[x].stp=0;//将当前第一个位置的步数标记为0步 
	q1.push(q[x]);//将第一个元素塞到队列 
	while(!q1.empty()){
		node t=q1.front();//拿到队头 
		q1.pop();
		sum+=t.w*t.stp;//把权值加到sum里 
		int L=t.lfte,R=t.right,F=t.fa;
		if(F!=0&&sg[F]==0){//如果当前节点的父节点有值，并且没有走过，则步数加一，进行标记，并将其塞到队列。下面同理 
			sg[F]=1;
			node t1=q[F];
			t1.stp=t.stp+1;
			q1.push(t1);
		}
		if(L!=0&&sg[L]==0){
			sg[L]=1;
			node t1=q[L];
			t1.stp=t.stp+1;
			q1.push(t1);
		}
		if(R!=0&&sg[R]==0){
			sg[R]=1;
			node t1=q[R];
			t1.stp=t.stp+1;
			q1.push(t1);
		}
	}
	 
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>q[i].w>>q[i].lfte>>q[i].right; 
		q[q[i].lfte].fa=i;//当前位置的左右孩子的父节点就是当前位置 
		q[q[i].right].fa=i;
	}
	for(int i=1;i<=n;i++){
		memset(sg,0,sizeof(sg));//初始化标记数组 
		sum=0;
		sg[i]=1;
		dfs(i);
		ant=min(ant,sum);
	}
	cout<<ant;
	return 0;
}