文章目录
- 思想
- 例题
- 1. 分成互质组
- 题目链接
- 题目描述
- 【解法一】
- 【解法二】
- 2. 小猫爬山
- 题目链接
- 题目描述
- 输入样例:
- 输出样例:
- 【思路】
- 【WA代码】
- 【AC代码】
思想
- 本质为两种搜索顺序:
- 枚举当前元素可以放入哪一组
- 枚举每一组可以放入哪些元素
- 操作为两种
- 放入当前组
- 新开一个组
例题
1. 分成互质组
题目链接
https://www.acwing.com/problem/content/1120/
题目描述
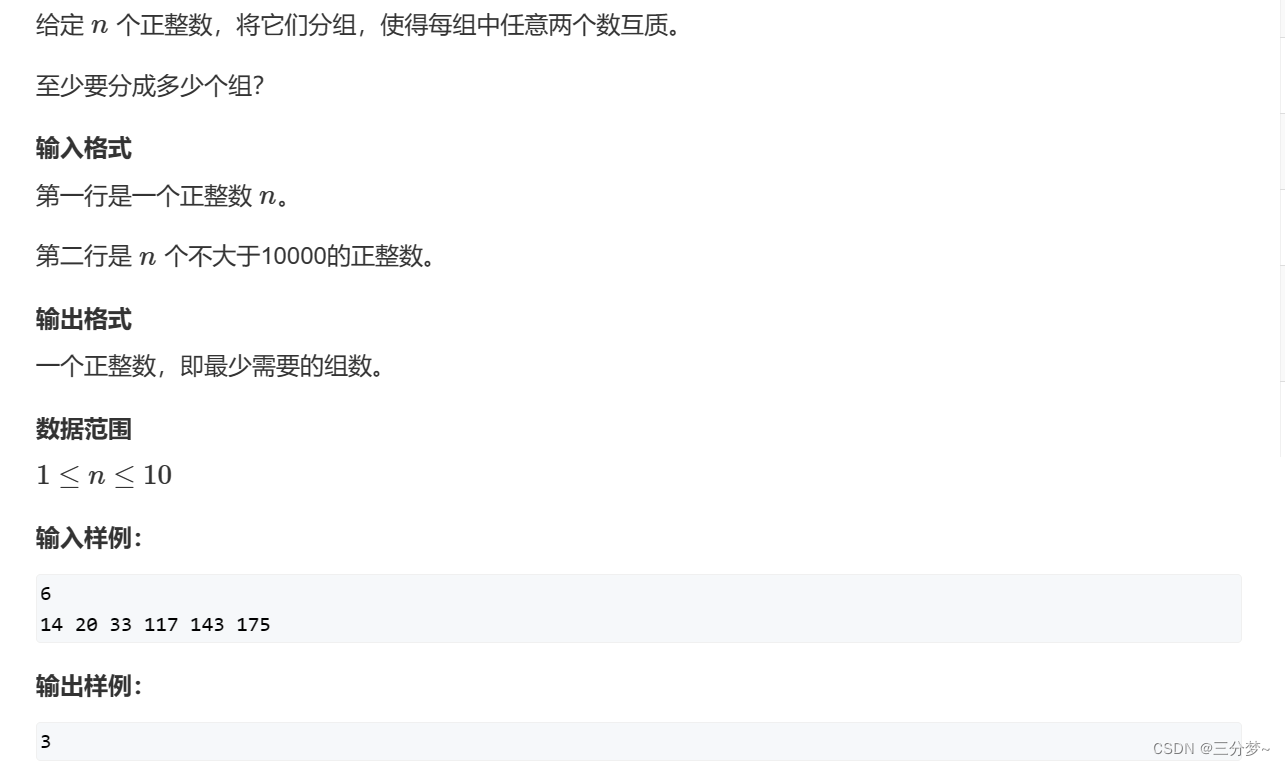
【解法一】
枚举每一组可以放哪些元素
#include <iostream>
using namespace std;
const int N = 11;
int g[N][N];
int a[N];
bool st[N];
int n;
int ans = N;
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
bool check(int g[], int x, int k) {
for(int i = 0; i < k; i ++)
if(gcd(g[i], x) > 1)
return false;
return true;
}
void dfs(int gu, int gid, int start, int cnt) {
if(gu >= ans) return ; //剪枝, 若当前分组大于答案,那么不如之前的也没必要枚举了
if(cnt == n) ans = min(ans, gu);
bool flag = true; //从start开始找,是否有元素不能入当前组
for(int i = start; i < n; i ++) {
if(!st[i] && check(g[gu], a[i], gid)) {
st[i] = true;
g[gu][gid] = a[i];
dfs(gu, gid + 1, i + 1, cnt + 1);
//恢复现场
st[i] = false;
flag = false;
}
}
//操作二:新开数组
if(flag) dfs(gu + 1, 0, 0, cnt);
}
int main() {
cin >> n;
for(int i = 0; i < n; i ++) cin >> a[i];
//当前在第几组,第几个数,从哪个位置开始选,已经选好几个数
dfs(1, 0, 0, 0);
cout << ans;
return 0;
}
【解法二】
枚举当前元素可以放入哪个组
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 10;
int a[N];
vector<int> g[N]; //互质组
int n;
int ans = N;
int gcd(int a, int b){
return b?gcd(b, a%b) : a;
}
bool check(int c,int x){
for(int i=0;i<g[c].size();i++){
if(gcd(g[c][i],x)>1) return false;
}
return true;
}
void dfs(int u, int k){ //当前为第u个数, 已开辟的组的个数
if(u==n){
ans=min(ans,k);
return;
}
//每个元素的方法即 -> 放到当前已经存在的组中 或者 放到新开的组中
//操作一:放入已经存在的组中
for(int i=0; i < k; i ++){
if(check(i, a[u])){
g[i].push_back(a[u]);
dfs(u + 1, k);
g[i].pop_back();
}
}
//可见这里的k代表着的是当前开辟数组的个数
//操作二:新开一个组
g[k].push_back(a[u]);
dfs(u+1, k + 1);
g[k].pop_back();
}
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
dfs(0, 0);
cout<<ans;
return 0;
}
2. 小猫爬山
题目链接
https://www.acwing.com/problem/content/167/
题目描述

输入样例:
5 1996
1
2
1994
12
29
输出样例:
2
【思路】
第一步很容易会误以为这是一道背包问题,不过看了眼数据范围,容量太大,而n的范围很小,故为一道dfs搜搜问题
这里根据数据范围我们必然需要优化,分析可以优化的点:

- ① 要求最小车辆,那么如果我们搜索某种决策时当前的车辆数已经大于
ans了,那么必然不是最优解,直接退出即可 - ② 对于
dfs决策时,要想使得决策的分支少点,那么从根开始越少的话,那么必然分支也会更少,想到从此处进行优化的话,那么若是优先考虑重量大的,可以实现,因为在已有的车辆中选择可放入的重量大的可选车辆少
下面展示代码:
【WA代码】

枚举每一组可以放入哪些元素
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n, W;
int w[N];
int g[N][N];
bool st[N];
int ans = N;
void dfs(int gu, int ct, int start, int cnt) {
if(gu >= ans) return ;
if(cnt == n) {
ans = min(ans, gu);
return;
}
bool flag = true; //判断是否可以放进去当前组
//操作一:加入当前组
for(int i = start; i < n; i ++) {
if(!st[i] && ct + w[i] <= W) {
st[i] = true;
dfs(gu, ct + w[i], start + 1, cnt + 1);
//恢复现场
st[i] = false;
flag = false;
}
}
//操作二:新开组
if(flag) dfs(gu + 1, 0, 0, cnt);
}
int main() {
cin >> n >> W;
for(int i = 0; i < n; i ++) cin >> w[i];
//为了使得决策少点,优化时间,选择先放重量大的
sort(w, w + n, greater<int>());
//从第gu个组开始,当前在判断第gid个数,已经匹配的数字, 从哪个数开始
dfs(1, 0, 0, 0);
cout << ans;
return 0;
}
【AC代码】
枚举当前元素可以放入哪些组
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n, W;
int w[N];
int sum[N]; //第i辆车的重量
bool st[N];
int ans = N;
void dfs(int u, int k) { //u代表当前遍历的数,k代表当前已有分组数量
if(k >= ans) return;
if(u == n) {
// ans = min(ans, k); //因为有上步条件制约,故不需要min
ans = k;
return;
}
//操作一:放入某个已有的车辆
for(int i = 0; i < k; i ++) {
if(sum[i] + w[u] <= W) {
sum[i] += w[u];
dfs(u + 1, k);
//恢复现场
sum[i] -= w[u];
}
}
//操作二: 放不下,新开车辆
sum[k] = w[u];
dfs(u + 1, k + 1);
sum[k] = 0;
}
int main() {
cin >> n >> W;
for(int i = 0; i < n; i ++) cin >> w[i];
//为了使得决策少点,优化时间,选择先放重量大的
sort(w, w + n, greater<int>());
dfs(0, 0);
cout << ans;
return 0;
}