下一篇将介绍整理各种聚类算法，包括k-means，GMM(Guassian Mixture Models, 高斯混合)，EM(Expectation Maximization，期望最大法)，Spectral Clustering(谱聚类)，Mean Shift(均值偏移)和DBSCAN(Density-Based Spatial Clustering of Applications with Noise)

在介绍这些聚类算法之前，需要熟悉一些基础的数学知识，比如说: SVD(奇异值分解)，Rayleigh Quotient(瑞利商)，Joint Probability(联合概率)，Conditional Probabliity(条件概率分布)，Marginalization(边缘分布)，Bayes rule(贝叶斯定理)，Directed Graphical Model(有向图)，Undirected Graphical Model(无向图)和Lagrange multiplier(拉格朗日乘子定理)。

1. 瑞利商

见文章PCA算法中2的瑞利商原理介绍。

2. 谱定理

见文章PCA算法中1的谱定理介绍。

3. 联合概率

• 分布函数,联合分布函数
  设$(X,Y)$是二维随机变量，对于任意实数$x,y$，二元函数:
  $$F(x,y)=P((X\le x)\cap (Y\le y))=P(X\le x,Y\le y)$$
  称为二维随机变量$(X,Y)$的分布函数，或称为随机变量X和Y的联合分布函数

• 二维随机变量的联合分布率
  

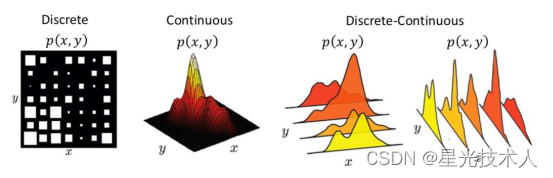
  • 二维离散型随机变量的联合分布率
    如果二维随机变量$(X,Y)$全部可能取到的值是有限对，则称$(X,Y)$是离散型的随机变量。设所有的可能取值为$(x_i,y_i),i,j=1,2,...,n$,则记$P(X=x_i,Y=y_j)=p_{ij}$为二维离散性随机变量$(X,Y)$的分布律，也可以叫做随机变量X和Y的联合分布律。

  • 二维连续型随机变量的联合分布
    如果随机变量X和Y的取值是连续的，记二维随机变量(X,Y)的分布函数为F(X,Y)，如果存在非负可积函数f(x,y)使对任意x,y有:
    $$F(x,y)={\int }_{-\infty }^y{\int }_{-\infty }^{x}f(u,v)dudv$$
    则称$(X,Y)$是连续型的二维随机变量，函数$f(x,y)$为二维连续型随机变量的概率密度，或称为随机变量X和Y的联合概率。

  • 二维离散-连续型随机变量的联合分布
    如果$X$是离散型随机变量，而 $Y$ 是连续型随机变量，则它们的联合分布可以用条件概率质量函数和条件概率密度函数来描述。
    假设$X$是离散型随机变量，取值集合为{$x_1.x_2,...,x_n$}。而$Y$是连续型随机变量，其概率密度函数为$f_y(Y)$(也叫做变量(X,Y)关于Y的边缘概率密度)。则二者的联合分布可以表示为：
    离散型$X$和连续型$Y$的联合概率函数$P\left(X=x_i,Y=y\right)$表示了在$X$取值为$x_i$ 的条件下，$Y$取值在为$Y\le y$的概率质量。这可以用条件概率函数来描述:
    $$P\left(X=x_i,Y=y\right)=P\left(Y=y\mid X=x_i\right)\cdot P\left(X=x_i\right)$$
    其中，$P\left(Y=y\mid X=x_i\right)$是在$X=x_i$的条件下$Y$取值为$y_j$的条件概率,$P\left(X=x_i\right)$是$X$取值为$x_i$的概率。
    这里的连续变量Y的概率密度函数，可以是不同的x对应不同的密度函数，也可以是把x作为了变量Y的概率密度函数的一个权重。
    连续型$Y$的条件概率密度函数$f_{Y\mid X}\left(y\mid x_i\right)$给出了在给定$X=x_i$的条件下, $Y$的概率密度函数。这可以用条件概率密度函数来描述:
    $$f_{Y\mid X}\left(y\mid x_i\right)=\frac{f_{XY}\left(x_i,y\right)}{P\left(X=x_i\right)}$$
    其中，$f_{XY}\left(x_i,y\right)$是$X$和$Y$的联合概率密度函数，$P\left(X=x_i\right)$是$X$取值为$x_i$的概率。可以结合上图理解，

4. 条件概率分布

可以结合上文0.3联合概率中的二维离散-连续型随机变量的联合分布来理解。只不过除此之外，还有二维离散型和二维连续性的条件概率分布，这都可以二维离散型的联合分布和二维连续型的联合分布对应起来。因为所有条件概率，无非就是两个变量已经确定下来一个。通用的公式描述如下：
条件概率是概率论中的一个重要概念，用于描述在给定某些条件下某个事件发生的概率。它的形式通常表示为$P(A\mid B)$，读作“在事件 B 发生的条件下事件 A 发生的概率”。

具体来说，条件概率指的是在已知某个事件 B 发生的情况下，事件 A 发生的概率。这种概率考虑了事件 B 的发生对事件 A 的影响，因此与简单的事件 A 的概率$P(A)$有所区别。

条件概率的计算公式为：
$$P(A\mid B)=\frac{P(A\cap B)}{P(B)}$$

其中，

• $P(A\mid B)$表示在事件 B 发生的条件下事件 A 发生的概率，也称为后验概率（posterior probability）。
• $P(A\cap B)$表示同时发生事件 A 和事件 B 的概率，称为事件 A 与事件 B 的交集概率。
• P(B) 表示事件 B 发生的概率，称为事件 B 的概率。
  条件概率的意义在于考虑了某个事件发生的背景信息或条件，从而更准确地评估事件发生的可能性。它在贝叶斯统计、机器学习、工程等领域中都有广泛的应用，例如在模式识别、信号处理、风险评估等方面都可以用到条件概率的概念和计算方法。

5. 边缘分布

边缘分布 (Marginal Distribution) 是概率论和统计学中的重要概念, 用于描述多维随机变量中单个变量的分布情况。边缘分布是从联合分布中抽取出某个或某些随机变量的概率分布, 而忽略其他随机变量的分布。

考虑一个多维随机变量 $\left(X_1,X_2,\dots ,X_n\right)$的联合分布, 称为联合概率分布。如果我们只关心其中的一部分变量, 比如 $X_1,X_2$ ， 那么从联合分布中抽取出 $X_1$ 的概率分布（忽略 $X_2$ 以及其他变量), 就得到了$X_1$的边缘分布。类似地, 我们也可以得到$X_2$的边缘分布。

边缘分布的计算可以通过对联合分布进行边际化 (Marginalization) 来实现。边际化是通过对联合分布中不感兴趣的变量进行积分或求和, 来获得感兴趣变量的边缘分布。

对于离散型随机变量 X 和 Y 的联合分布, 边缘化可以表示为:

$$P\left(X=x_i\right)=\sum _{j}P\left(X=x_i,Y=y_j\right)$$

对于连续型随机变量 X 和 Y 的联合概率密度函数 f(x, y) , 边缘化可以表示为:
$$f_X(x)={\int }_{-\infty }^{\infty }f(x,y)dy$$
其中，$f_X(x)$是 $X$ 的边缘概率密度函数。

边缘分布的概念在概率统计中非常重要, 它可以帮助我们理解单个变量的分布特征, 从而进行更精确的推断和分析

6. 贝叶斯定理

什么是似然度？

7. 有向图

有向图（Directed graph）是图论中的一种重要概念，在图形建模（Graphical Modeling）中起着关键作用。以下是有向图的中文介绍：

有向图是由一组顶点（节点）和一组有方向的边（箭头）组成的图形结构。每条边从一个顶点指向另一个顶点，表示了一个有向关系或者流向。有向图中的每个节点表示一个变量或者事件，而有向边则表示这些变量或事件之间的直接影响或关系。

有向图可以用来表示因果关系、依赖关系、流程控制等各种情况。在图形建模中，有向图常用于表示贝叶斯网络（Bayesian networks）或者因果图（Causal graphs）。贝叶斯网络是一种基于概率的图模型，用于表示变量之间的依赖关系和概率分布；因果图则用于表示因果关系，帮助理解事件或变量之间的因果链条。

有向图中的一些重要概念包括：

1. 父节点和子节点： 一个节点的父节点是指向它的节点，而子节点是由它指向的节点。
2. 入度和出度： 节点的入度是指向它的边的数量，而出度是由它指向的边的数量。
3. 路径和环路： 路径是顺序连接的边和节点序列，环路是形成闭合回路的路径。
4. 拓扑排序： 有向图中节点的线性排序，使得所有的有向边从左到右都是指向右边的。
   总之，有向图是图形建模中非常重要的一种图形结构，用于表示变量之间的因果关系、依赖关系和流程控制，具有广泛的应用领域和实际意义。

重点
有向图节点之间的连接代表了条件关系，如下图：

事件B发生的提前是事件A已经发生。比如事件A表示该这个人是个男孩子，事件B就是这个男孩子的头发是黑色还是红色。这与这个人的头发是黑色还是红色的概率是不同的。如果两者之间相互独立，没有联系，就不存在有向图之间的联系(边)。

8. 拉格朗日乘子定理

现在有个基础的数学问题: $f(x,y)$表示自变量为$x,y$的函数，求$f(x,y)$在限定条件为$g(x,y)=0$下的最大值。也就是说自变量的取值区域被限制了。公式描述为:
$$maxf(x,y),s.t.g(x,y)=0$$

问题转义： 试想$f(x,y)和g(x,y)$都是一个曲面，现在设定了自变量只能取曲面$g(x,y)$上$g(x,y)=0$的值，见下图：

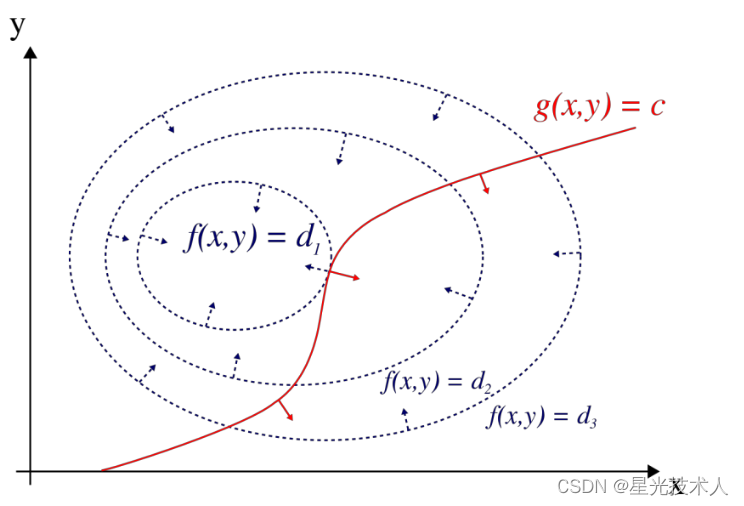
绘制出曲面的等高线，虚线代表等高线，$f(x.y)$的变量可行域是这个条红线。可见$当$f(x,y)$取的最最值的时候，两者的梯度刚好相反，所以对于这种有约束的最值问题，拉格朗日的统一解法为：