LeetCode题练习与总结：合并区间--56

news2024/12/23 10:15:22

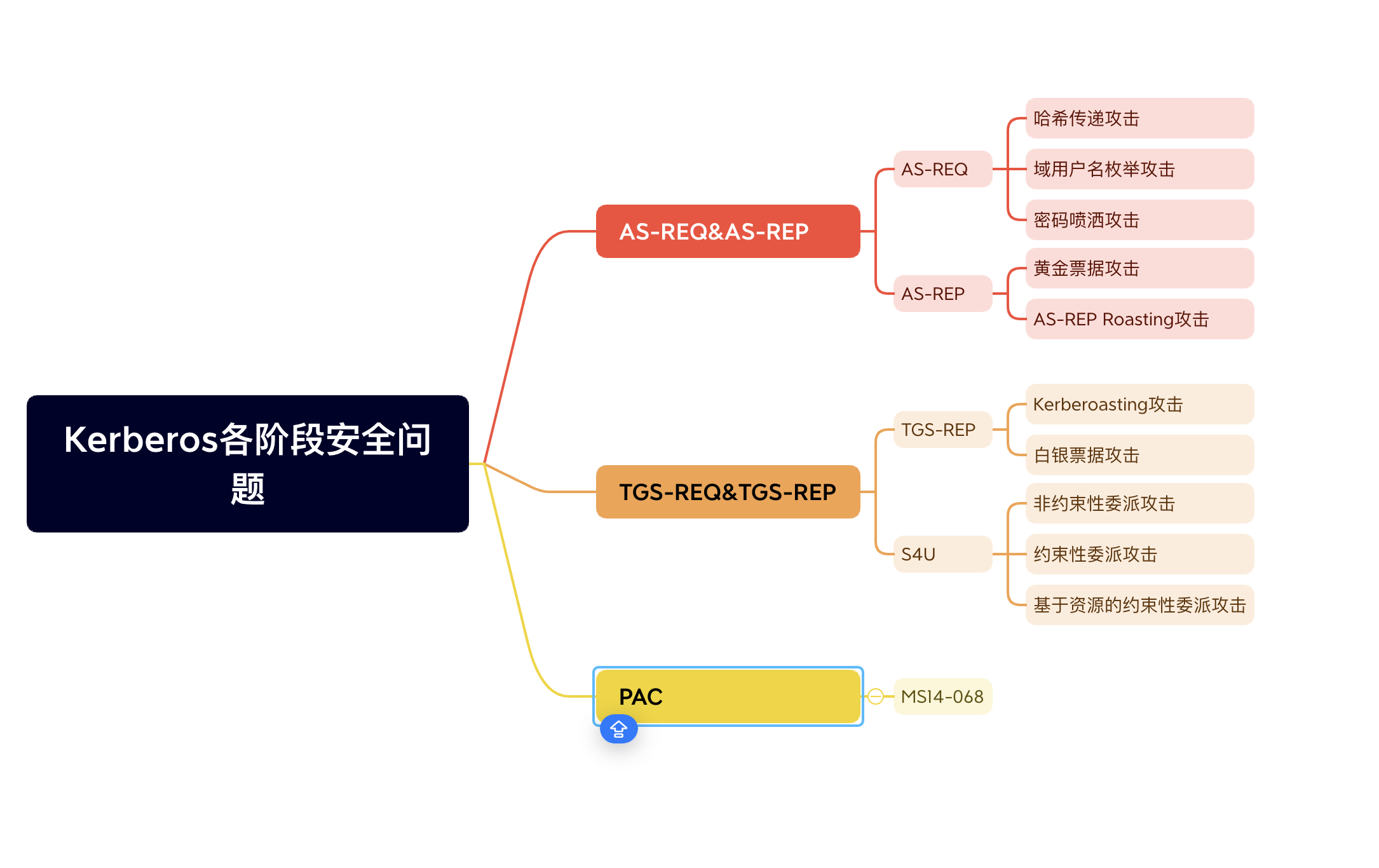
一、题目描述

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

二、解题思路

对区间数组 intervals 按起始点进行排序。
初始化两个指针，一个用于遍历区间 i，另一个用于记录合并后的区间的开始位置 j。
创建一个新的 List 来存储合并后的区间，这样可以动态地添加新的区间而不用担心数组越界的问题。
遍历排序后的区间，比较当前区间与上一个区间是否有重叠。
如果有重叠，更新上一个区间的结束点为当前区间结束点和上一个区间结束点的最大值。
如果没有重叠，将上一个区间添加到结果列表中，并将当前区间作为新的区间。
遍历结束后，将最后一个区间也添加到结果列表中。
将结果列表转换为二维数组并返回。

三、具体代码

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals == null || intervals.length < 2) {
            return intervals;
        }

        // Sort the intervals by the start point
        Arrays.sort(intervals, (a, b) -> a[0] - b[0]);

        List<int[]> mergedIntervals = new ArrayList<>();
        int i = 0;

        // Iterate through the intervals
        while (i < intervals.length) {
            int start = intervals[i][0];
            int end = intervals[i][1];
            int j = i + 1;

            // Merge overlapping intervals
            while (j < intervals.length && intervals[j][0] <= end) {
                end = Math.max(end, intervals[j][1]);
                j++;
            }

            // Add the merged interval to the list
            mergedIntervals.add(new int[]{start, end});
            i = j;
        }

        // Convert the list of intervals to a 2D array
        int[][] result = new int[mergedIntervals.size()][2];
        for (int k = 0; k < mergedIntervals.size(); k++) {
            result[k] = mergedIntervals.get(k);
        }

        return result;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

对区间进行排序：O(n log n)，其中 n 是区间的数量。这是因为 Arrays.sort 使用的是双轴快速排序算法，其时间复杂度为 O(n log n)。
遍历和合并区间：O(n)。在最坏的情况下，每个区间都与其他区间重叠，因此我们需要遍历所有的区间，但是每个区间只被处理一次，所以这部分的时间复杂度是线性的。
将 List 转换为二维数组：O(k)，其中 k 是合并后的区间数量。这通常小于等于原始区间的数量 n。
综上所述，总的时间复杂度是 O(n log n) + O(n) + O(k)，由于 k 通常小于 n，所以主要的时间复杂度贡献是 O(n log n)。

2. 空间复杂度

存储排序后的区间：O(n)，因为我们需要存储所有的原始区间。
存储合并后的区间：O(k)，其中 k 是合并后的区间数量。在最坏的情况下，所有的区间都重叠，合并后的区间数量为1，这时空间复杂度为 O(n)。在最好的情况下，没有重叠的区间，合并后的区间数量等于原始区间的数量，这时空间复杂度也是 O(n)。
因此，总的空间复杂度是 O(n) + O(k)，主要的空间复杂度贡献是 O(n)。

五、总结知识点

数组排序 (Arrays.sort): 使用Java标准库中的 Arrays.sort 方法对区间数组按照起始点进行排序。这是合并重叠区间的前提，因为只有排序后才能正确地识别和处理重叠的区间。
Lambda表达式: 在排序方法中使用了Lambda表达式 (a, b) -> a[0] - b[0] 作为比较器（Comparator），它比较两个区间的起始点，用于排序。
ArrayList: 使用 ArrayList 来动态存储合并后的区间。由于合并过程中可能减少区间的数量，使用动态数组可以避免在编译时确定数组大小，从而提高代码的灵活性。
循环控制: 代码中使用了 while 循环来遍历和合并区间。通过两个嵌套的循环（外循环遍历所有区间，内循环合并重叠区间）来实现合并逻辑。
条件判断: 在内循环中，使用条件判断 intervals[j][0] <= end 来检查当前区间是否与已合并区间重叠。
数学运算 (Math.max): 使用 Math.max 函数来获取两个区间结束点的最大值，这是合并区间时确定新区间结束点的方法。
数组和集合的转换: 最后，代码将 ArrayList 转换为二维数组。这是为了满足题目要求的输出格式，同时也是Java中常见的数据结构转换操作。
边界检查: 在合并区间的过程中，代码通过检查 j < intervals.length 来避免数组越界异常。
返回值处理: 如果输入的区间数组为空或者只包含一个区间，直接返回原数组，这是处理边界情况的一种简单有效的方法。