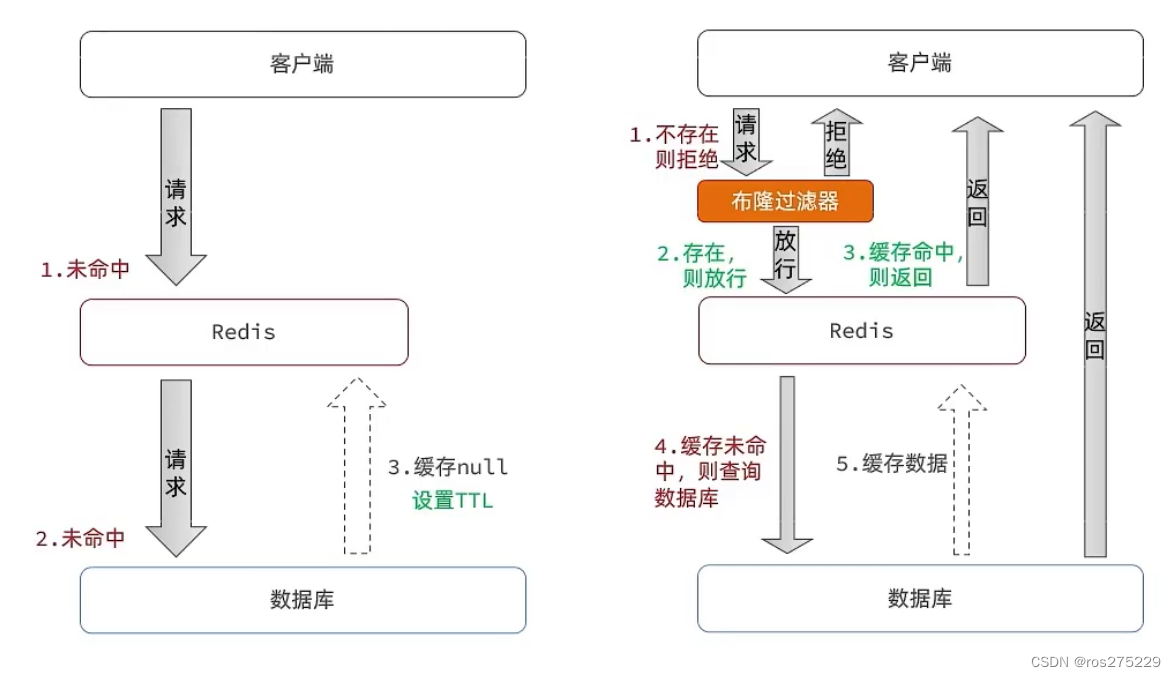
缓存穿透 ：缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在，这样缓存永远不会生效，这些请求都会打到数据库。

常见的解决方案有两种：

• 缓存空对象

  • 优点：实现简单，维护方便

  • 缺点：

    • 额外的内存消耗

    • 可能造成短期的不一致

• 布隆过滤

  • 优点：内存占用较少，没有多余key

  • 缺点：

    • 实现复杂

    • 存在误判可能

缓存空对象思路分析：当我们客户端访问不存在的数据时，先请求redis，但是此时redis中没有数据，此时会访问到数据库，但是数据库中也没有数据，这个数据穿透了缓存，直击数据库，我们都知道数据库能够承载的并发不如redis这么高，如果大量的请求同时过来访问这种不存在的数据，这些请求就都会访问到数据库，简单的解决方案就是哪怕这个数据在数据库中也不存在，我们也把这个数据存入到redis中去，这样，下次用户过来访问这个不存在的数据，那么在redis中也能找到这个数据就不会进入到缓存了

布隆过滤：布隆过滤器其实采用的是哈希思想来解决这个问题，通过一个庞大的二进制数组，走哈希思想去判断当前这个要查询的这个数据是否存在，如果布隆过滤器判断存在，则放行，这个请求会去访问redis，哪怕此时redis中的数据过期了，但是数据库中一定存在这个数据，在数据库中查询出来这个数据后，再将其放入到redis中，

假设布隆过滤器判断这个数据不存在，则直接返回

这种方式优点在于节约内存空间，存在误判，误判原因在于：布隆过滤器走的是哈希思想，只要哈希思想，就可能存在哈希冲突

小总结：

缓存穿透产生的原因是什么？

• 用户请求的数据在缓存中和数据库中都不存在，不断发起这样的请求，给数据库带来巨大压力

缓存穿透的解决方案有哪些？

• 缓存null值

• 布隆过滤

• 增强id的复杂度，避免被猜测id规律

• 做好数据的基础格式校验

• 加强用户权限校验

• 做好热点参数的限流