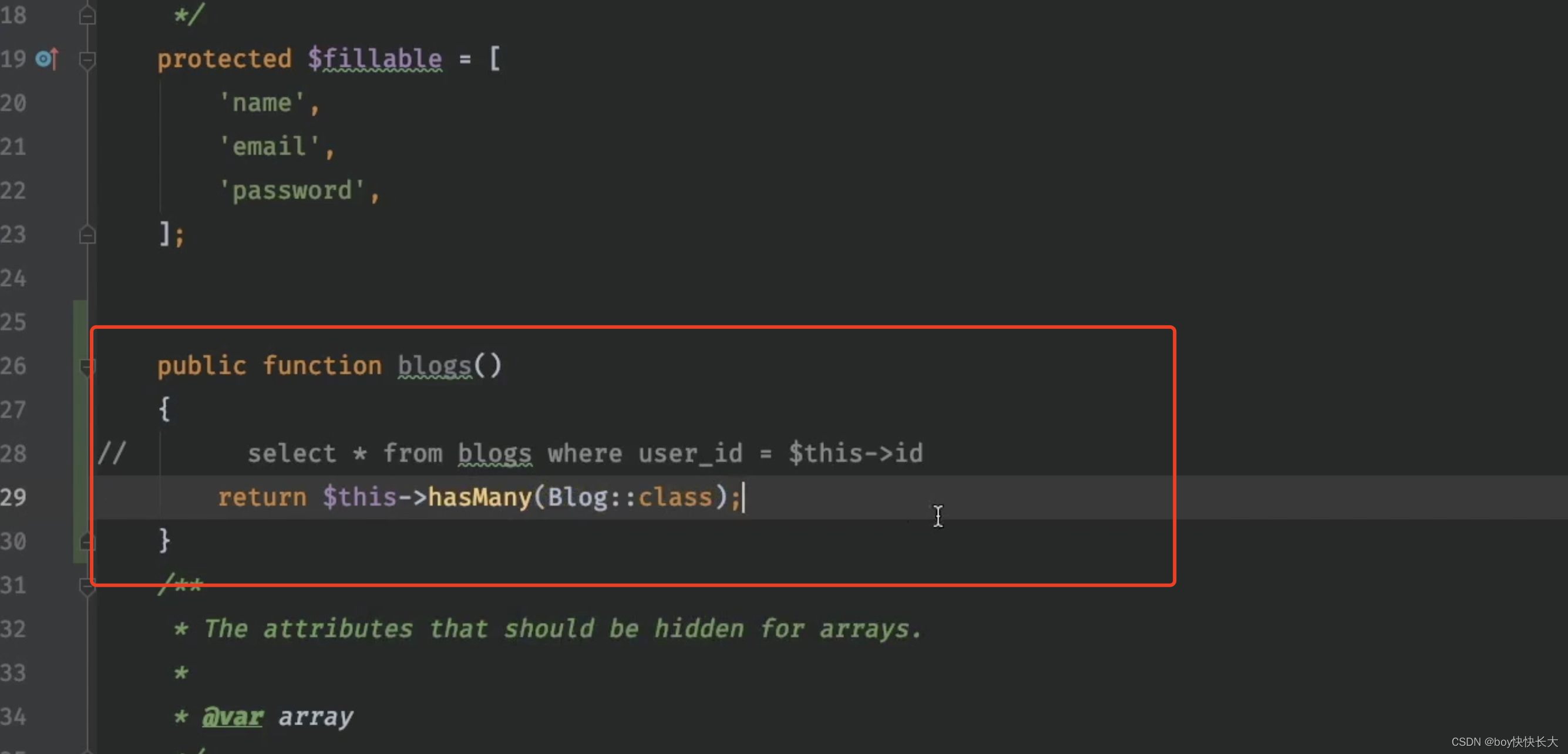
01 基本想法
单音素HMM模型不能很好的应对自然说话人发音时的渐变过程,比如从一个音素转换到另一个音素时会存在协同发音现象。因此语音识别的先驱者提出了上下文建模概念,即使用中心音素(单因素)和前后两个音素组成三音素对每一个发音进行建模。三因素和单因素一样都是使用三状态的HMM,只是将原来的单因素的模型扩充了。比如原先用40个单因素进行建模,使用三因素时,理论上需要40x40x40个音素,总共40x40x40x3个状态。这样盲目扩充造成了参数过多,训练数据不足的问题。因此需要将相似的三因素进行合并。一种高效的方法是构造二叉树模型,通过问题将状态集逐步划分,叶子节点中的状态具有相似性,可以用同样的输出概率模型表示。
为每一个中心音素的每一个状态构建一个决策树,树的每一个节点对应一个yes/no的问题。在树的根节点,所有的状态的输出模型共享相同的参数。通过问题对状态进行划分,最终叶子节点对应具有相同输出概率模型的状态。问题是从一个庞大的预先定义的问题集中选择,也可以自动生成。本文介绍了通过决策树自动生成问题的方法
02 使用决策树建模上下文相关的HMM
- 将单音素模型的HMM与训练数据(特征向量)对齐(训练单因素模型);
- 对于每一个特征向量,可以找到它对于的音素和左、右音素。
- 对于每一个音素,构建一个决策树。
- 叶子节点就是上下文依赖的模型(一个叶子节点状态可绑定到相同的高斯模型上)
在树的构造过程中,使用对角高斯模型估计声学特征向量的似然概率
03 计算状态集的似然概率
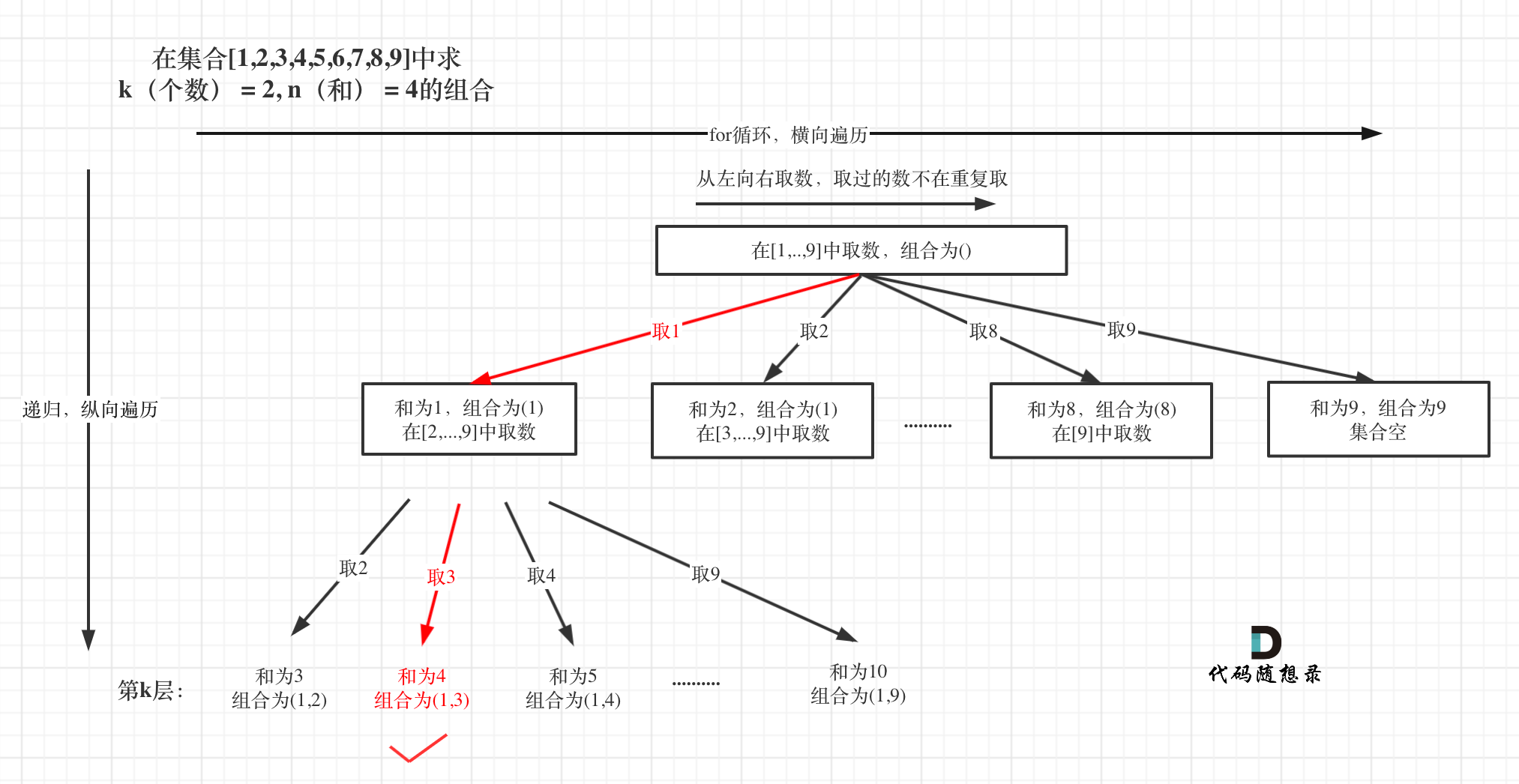
已知Y,
![]()
Y是独立的p维声学特征向量组成的序列,这些特征向量是同一个单因素的某个状态产生的,这个状态对应的输出概率分布用单个对角高斯分布表示,均值是,方差是
(注意由于y1,y2,...yn是p维向量,所以这里的均值也是p维,方差也是p维)。每一个y1属于一个三音素模型,这样Y对应于一个三因素状态集(由多个中心音素相同的三音素组成)。这可理解为将输出概率分布复制到没有绑定的三音素模型的概率分布上。我们知道未绑定状态前,三音素模型的个数是远大于单因素模型个数的。绑定的过程就是减少三因素模型的个数,从而减小参数量
我们首先计算状态集分裂前这n个p维特征向量的似然概率:

通过最大似然估计,得到均值和方差的估计:
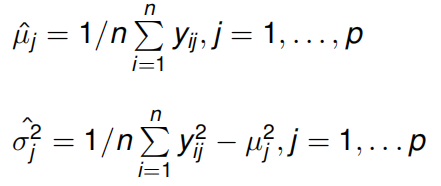
最大似然可写成:
![]()
因为

所以似然概率可以进一步写为:

04 二叉树分裂
Q是对状态集的一种划分,同时将Y分割成左、右两个子样本集和
,对应的大小为
和
,
最好的问题是能够最大化![]()
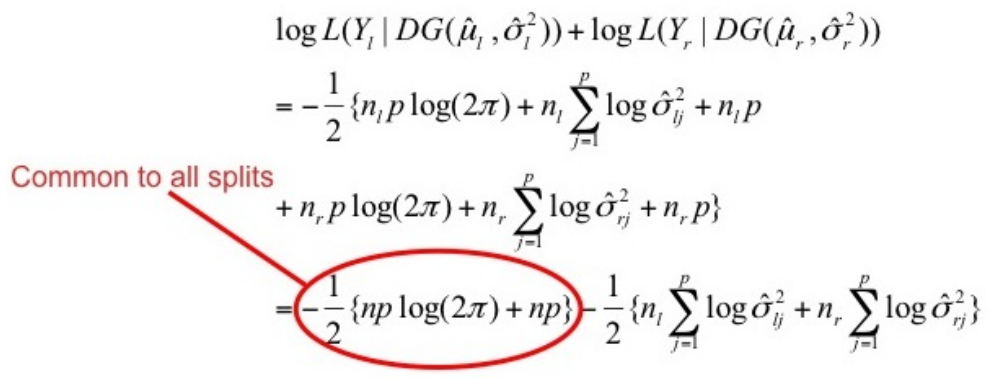
最好的问题Q可以最小化

其中
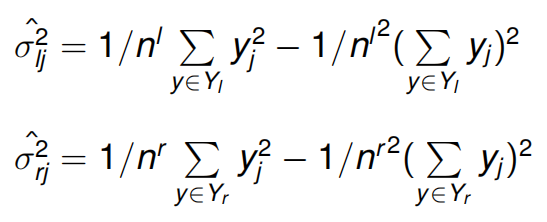






![[StartingPoint][Tier1]Crocodile](https://img-blog.csdnimg.cn/img_convert/6a6e016ae303f164f5fb76e63ec0f07b.jpeg)