原文链接:R语言技能 | 不同数据类型的转换
本期教程
写在前面
今天是4月份的第一天,再过2天后再一次迎来清明小假期。木鸡大家是否正常放假呢?
我们在使用R语言做数据分析时,会一直对数据进行不同类型的转换,有时候会被自己弄晕掉,那么就只能一次一次的去解决,去寻找,去学习相关的知识点。
虽然,目前很多的云平台都能全自动化的给你绘图,很方便,但是自己依旧喜欢自己使用R来画,这个过程可能会花费很多的时间,但是自己在使用后会有一定的收获,至少让自己的大脑得以运转。
这个大脑长时间不用,当你使用时会很迟钝,木鸡大家是否有类似的情况。
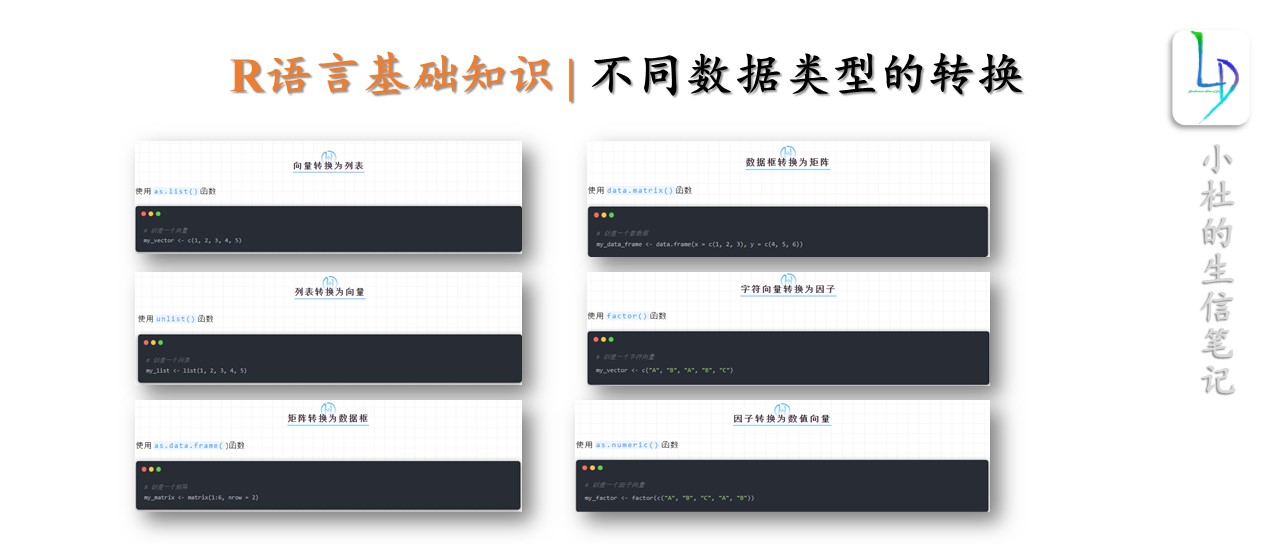
向量转换为列表
使用as.list()函数
# 创建一个向量
my_vector <- c(1, 2, 3, 4, 5)
[1] 1 2 3 4 5
# 转换为列表
my_list <- as.list(my_vector)
> my_list
[[1]]
[1] 1
[[2]]
[1] 2
[[3]]
[1] 3
[[4]]
[1] 4
[[5]]
[1] 5
列表转换为向量
使用unlist()函数
# 创建一个列表
my_list <- list(1, 2, 3, 4, 5)

# 转换为向量
my_vector <- unlist(my_list)

数据框转换为矩阵
使用data.matrix()函数
# 创建一个数据框
my_data_frame <- data.frame(x = c(1, 2, 3), y = c(4, 5, 6))

# 转换为矩阵
my_matrix <- data.matrix(my_data_frame)

矩阵转换为数据框
使用as.data.frame()函数
# 创建一个矩阵
my_matrix <- matrix(1:6, nrow = 2)

# 转换为数据框
my_data_frame <- as.data.frame(my_matrix)

字符向量转换为因子
使用factor()函数
# 创建一个字符向量
my_vector <- c("A", "B", "A", "B", "C")

# 转换为因子
my_factor <- factor(my_vector)

数值向量转换为字符向量
使用as.character()函数
# 创建一个数值向量
my_vector <- c(1, 2, 3, 4, 5)

# 转换为字符向量
my_character_vector <- as.character(my_vector)

因子转换为数值向量
使用as.numeric()函数
# 创建一个因子向量
my_factor <- factor(c("A", "B", "C", "A", "B"))

# 转换为数值向量
my_numeric_vector <- as.numeric(my_factor)

原文链接:R语言技能 | 不同数据类型的转换
若我们的分享对你有用,希望您可以点赞+收藏+转发,这是对小杜最大的支持。
往期文章:
1. 复现SCI文章系列专栏
2. 《生信知识库订阅须知》,同步更新,易于搜索与管理。
3. 最全WGCNA教程(替换数据即可出全部结果与图形)
-
WGCNA分析 | 全流程分析代码 | 代码一
-
WGCNA分析 | 全流程分析代码 | 代码二
-
WGCNA分析 | 全流程代码分享 | 代码三
-
WGCNA分析 | 全流程分析代码 | 代码四
-
WGCNA分析 | 全流程分析代码 | 代码五(最新版本)
4. 精美图形绘制教程
- 精美图形绘制教程
5. 转录组分析教程
-
转录组上游分析教程[零基础]
-
一个转录组上游分析流程 | Hisat2-Stringtie
6. 转录组下游分析
-
批量做差异分析及图形绘制 | 基于DESeq2差异分析
-
GO和KEGG富集分析
-
单基因GSEA富集分析
-
全基因集GSEA富集分析
小杜的生信筆記 ,主要发表或收录生物信息学的教程,以及基于R的分析和可视化(包括数据分析,图形绘制等);分享感兴趣的文献和学习资料!!