要求

代码

1. 导入模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

2. 导入数据

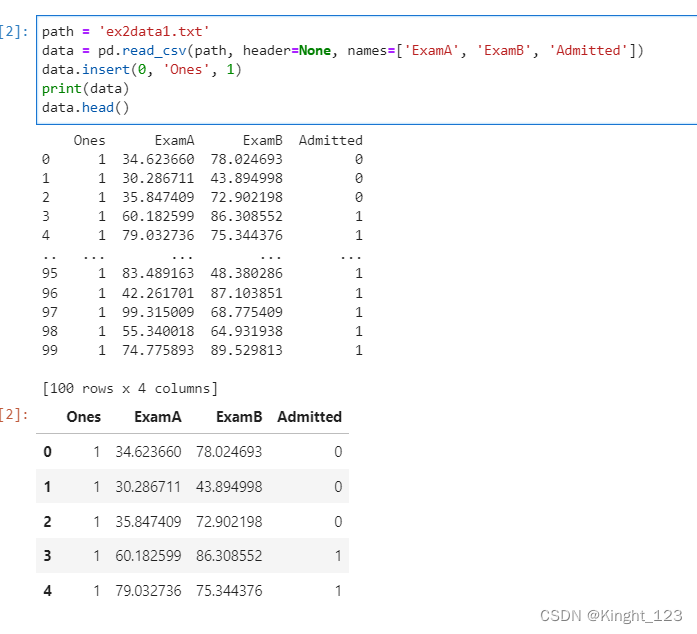
path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['ExamA', 'ExamB', 'Admitted'])
data.insert(0, 'Ones', 1)
print(data)
data.head()

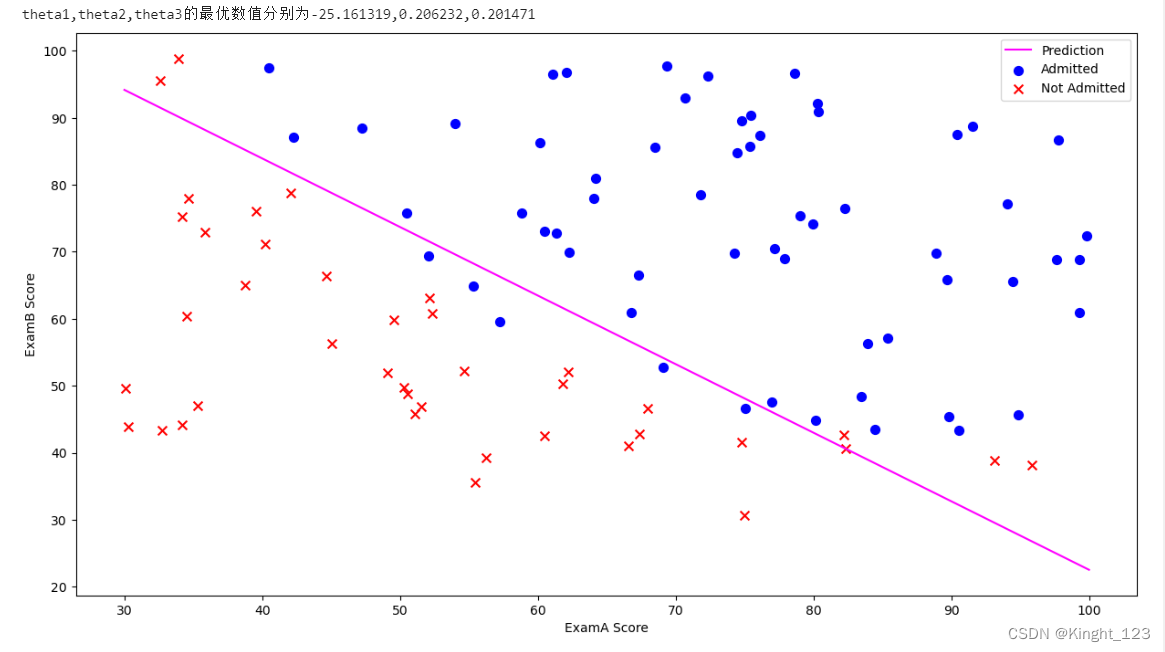
3. 求解theat的最优值,画出样本的位置和决策边界。

"""
函数：sigmoid函数(假设函数)
"""

# 定义sigmoid函数
def sigmoid(z):
    return 1.0 / (1 + np.exp(-z))

ls = []  # 用来存储每次迭代代价函数的数值
# 定义代价函数
def cost(theta, X, y):
    global ls
    theta = np.matrix(theta)  # 转换成为一个矩阵
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    ls.append(np.sum(first - second) / (len(X)))
    return np.sum(first - second) / (len(X))


# 定义梯度下降函数
def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    parameters = int(theta.ravel().shape[1])
    
    grad = np.zeros(parameters)
    error = sigmoid(X * theta.T) - y
    for i in range(parameters):
        term = np.multiply(error, X[:, i])
        grad[i] = np.sum(term) / len(X)
    return grad


# 处理数据
cols = data.shape[1]
X = data.iloc[:, 0:cols - 1]
y = data.iloc[:, cols - 1:cols]
theta = np.zeros(3)
# 转换X，y的类型
X = np.array(X.values)
y = np.array(y.values)



result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
print(f"theta1,theta2,theta3的最优数值分别为{result[0][0]:.6f},{result[0][1]:.6f},{result[0][2]:.6f}")


# 决策边界
plotting_x1 = np.linspace(30, 100, 100)
plotting_h1 = (- result[0][0] - result[0][1] * plotting_x1) / result[0][2]
positive = data[data['Admitted'].isin([1])]  # 将所有为1的行单独存放在positive
negative = data[data['Admitted'].isin([0])]  # 将所有为0的行单独存放在negative
fig, ax = plt.subplots(figsize=(15, 8))
ax.plot(plotting_x1, plotting_h1, 'fuchsia', label='Prediction')
ax.scatter(positive['ExamA'], positive['ExamB'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['ExamA'], negative['ExamB'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('ExamA Score')
ax.set_ylabel('ExamB Score')
plt.show()

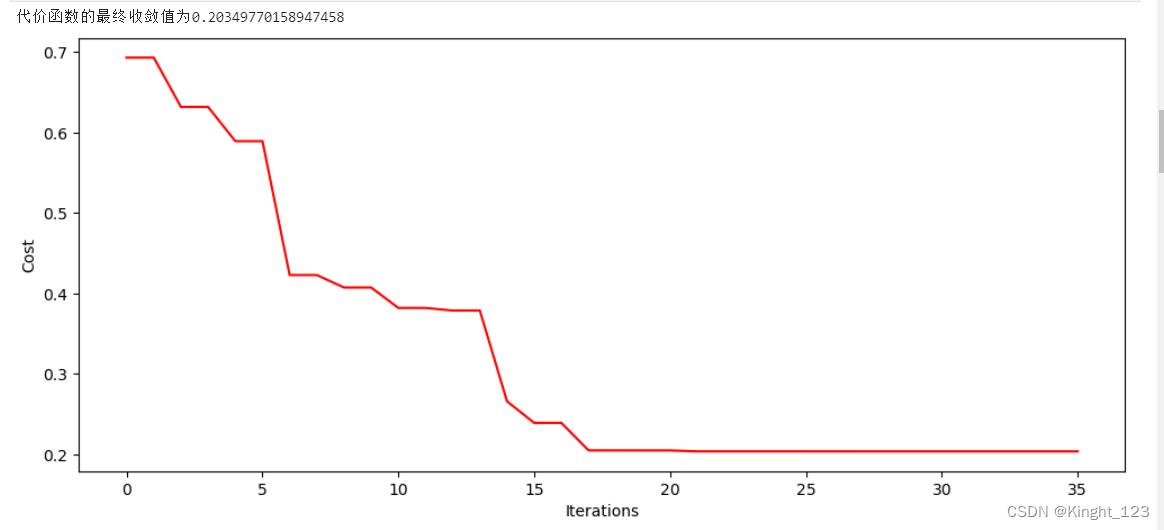
4. 画出迭代函数随迭代次数变化的曲线,代价函数最终的收敛值

# 画出代价函数随迭代次数变化的曲线
print(f"代价函数的最终收敛值为{ls[-1]}")
fig, ax = plt.subplots(figsize=(12, 5))
ax.plot(np.arange(len(ls)), ls, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
plt.show()

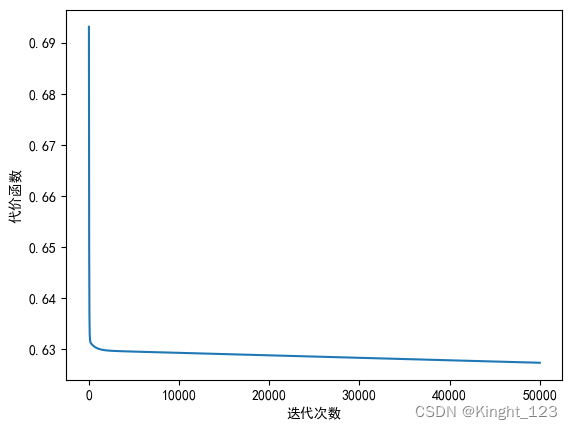
5.比较三种学习率的代价函数随迭代次数变化的曲线

def sigmod(z):
    return 1.0 / (1.0 + np.exp(-z))

def J(theta,X,Y,theLambda=0):
    m,n=X.shape
    h=sigmoid(np.dot(X,theta))
    J=(-1.0/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))+(theLambda/(2.0*m))*np.sum(np.square(theta[1:]))
    
    if np.isnan(J[0]):
        return np.inf
    return J.flatten()[0]

def gradient(X,y,options):
    """
    options.alpha 学习率
    options.theLambda 正则化参数λ
    options.maxloop 最大迭代次数
    options.epsilon  判断收敛的条件
    options.method
        -'sgd' 随机梯度下降
        -'bgd' 批量梯度下降
    """
    m,n=X.shape
    #初始化模型参数，n个特征对应n个参数
    theta=np.zeros((n,1))
    
    error=J(theta,X,y)#当前误差
    errors=[error,] #迭代每一轮的误差
    thetas=[theta,] #
    
    alpha=options.get('alpha',0.01)
    epsilon=options.get('epsilon',0.0000000001)
    maxloop=options.get('maxloop',1000)
    theLambda=float(options.get('theLambda',0))
    method=options.get('method','bgd')
    
    def _sgd(theta):
        count=0
        converged=False
        while count<maxloop:
            if converged:
                break
            #随机梯度下降，每一个样本都要更新
            for i in range(m):
                h=sigmoid(np.dot(X[i].reshape((1,n)),theta))
                theta=theta-alpha*((1.0/m)*X[i].reshape(n,1)*(h-y[i])+(theLambda/m)*np.r_[[[0]],theta[1:]])
                thetas.append(theta)
                error=J(theta,X,y,theLambda)
                errors.append(error)
                if abs(errors[-1]-errors[-2])<epsilon:
                    converged=True
                    break
            count+=1
        return thetas,errors,count
    
    def _bgd(theta):
        count=0
        converged=False
        while count < maxloop:
            if converged:
                break
                
            h=sigmoid(np.dot(X,theta))
            
            theta=theta-alpha*((1.0/m)*np.dot(X.T,(h-y))+(theLambda/m)*np.r_[[[0]],theta[1:]])
            
            thetas.append(theta)
            error=J(theta,X,y,theLambda)
            errors.append(error)
            
            count +=1
            
            if abs(errors[-1]-errors[-2])<epsilon:
                converged=True
                break
        return thetas,errors,count
    
    methods={'sgd':_sgd,'bgd':_bgd}
    return methods[method](theta)

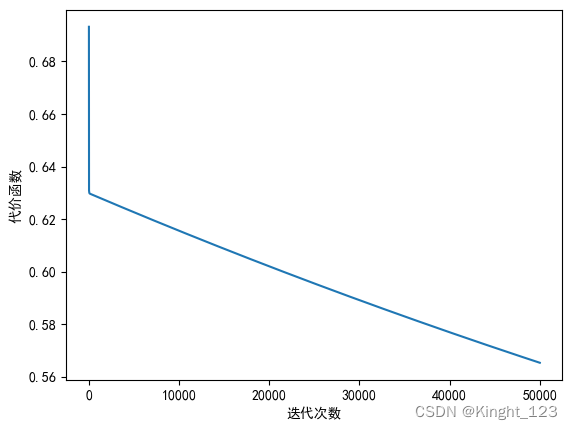
5.1 学习率为0.0003

options={
    'alpha':  0.0003, #学习率过大会产生局部震荡
    'epsilon':0.00000000001,
    'maxloop':50000,
    'method':'bgd'
}

thetas,errors,iterationCount=gradient(X,y,options)

plt.rcParams['font.sans-serif']='SimHei' #画图正常显示中文
plt.rcParams['axes.unicode_minus']=False #决绝保存图像是负号‘-’显示方块的问题
plt.plot(range(len(errors)),errors)
plt.xlabel("迭代次数")
plt.ylabel("代价函数")
plt.show()

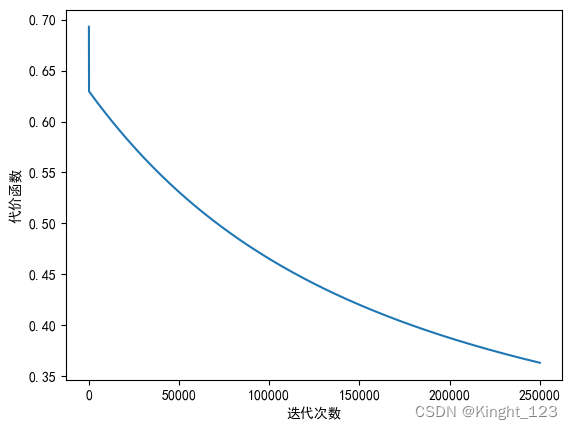
5.2 学习率为0.0005

options={
    'alpha':  0.0005, #学习率过大会产生局部震荡
    'epsilon':0.0000001,
    'maxloop':250000,
    'method':'bgd'
}

thetas,errors,iterationCount=gradient(X,y,options)

plt.rcParams['font.sans-serif']='SimHei' #画图正常显示中文
plt.rcParams['axes.unicode_minus']=False #决绝保存图像是负号‘-’显示方块的问题
plt.plot(range(len(errors)),errors)
plt.xlabel("迭代次数")
plt.ylabel("代价函数")
plt.show()

5.3 学习率为0.00001

options={
    'alpha':  0.00001, #学习率过大会产生局部震荡
    'epsilon':0.0000000001,
    'maxloop':50000,
    'method':'bgd'
}

thetas,errors,iterationCount=gradient(X,y,options)

plt.rcParams['font.sans-serif']='SimHei' #画图正常显示中文
plt.rcParams['axes.unicode_minus']=False #决绝保存图像是负号‘-’显示方块的问题
plt.plot(range(len(errors)),errors)
plt.xlabel("迭代次数")
plt.ylabel("代价函数")
plt.show()