转上一节:
http://t.csdnimg.cn/ql5Cd![]() http://t.csdnimg.cn/ql5Cd
http://t.csdnimg.cn/ql5Cd
课程内容提要:
6:知识点考点详解
6.1:线性结构
通常分析时间复杂度的方法是从算法中选取-种对于所研究的问题来说是基本运算的操作,以
该操作重复执行的次数作为算法的时间度量。一般来说, 算法中原操作重复执行的次数是规模n的
某个函数T(n)。
空间复杂度是指对一个算法在运行过程中临时占用存储空间大小的度量。一个算法的空间复
杂度只考虑在运行过程中为局部变量分配的存储空间的大小。
思考:求1+2+... +100的哪个算法更快?占用空间更少?
算法1:inti= (1+100)*100/2。只要运算1次。需要1个变量。
算法2: for循环执行100次。要运算n次。需要多个变量。
由于许多情况下要精确计算T(n)是困难的,因此引入了渐进时间复杂度在数量上估计一个算法的执
行时间。其定义如下:
如果存在两个常数c和m,对于所有的n,当n≥m时有f(n)≤Cg(n), 则有f(n)=O(g(n))。 也就是说,随着n
的增大, f(n)渐进地不大于g(n)。例如:一个程序的实际执行时间为,求其渐
进时间复杂度。随着n不断增加,n的影响很小。时间主要由
决定,则T(n)的渐进时间复杂
度就是O(),把常量值去掉。
常见的对算法执行所需
时间的度量:
技巧:把n=10代入即可。
(1)常数级时间复杂度0(1)
1)单个语句
如: K=0;
2)整个程序都没有循环语句,或复杂函数的调用

(2)时间复杂度O(n)

(3)时间复杂度O(n2)

思考: O () ?依此类推
(4)时复杂度O()


(5)时间复杂度O()
典型代表:堆排序,每次重建堆的时间复杂度是log2n, n个元基本上就是nlog2n.
(6)时间复杂度O()
典型代表:判断是否包含指定子序列,LCS最长公共子序列、钢管切割问题,动态规划法自顶向
下,时间复杂度为O()。
6.2:查找算法
考点1:顺序查找
顺序查找的思想:将待查找的关键字为key的元素从头到尾与表中元素进行比较,如果中间存在关健
字为key的元素,.则返回查找成功;否则,返回查找失败。
查找成功时,顺序查找的平均查找长度为(等概率情况下) :

考点2:二分查找
二分法查找的基本思想是:R[Iow,......,high]是当前的查找区)
(1)确定该区间的中点位置:mid=[(low+high)/2];
(2)将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区
间,继续二分查找,具体方法如下:
若R[mid].key > k,则由表的有序性可知R[mid,…,n].key均大于k,因此若表中存在关键字等于k的
结点,则该结点必定是在位置mid左边的子表R[low,…,mid-1]中。因此,新的查找区间是左子表
R[low,…,high],其中high=mid-1。
若R[mid].key<k,则要查找的k必在mid的右子表R[mid+1,…,high]中,即新的查找区间是右子表
R[low,…,high],其中low=mid+1。
若R[mid].key=k,则查找成功,算法结束。
(3)下一次查找是针对新的查找区间进行,重复步骤(1) 和(2)。
(4)在查找过程中,low逐步增加,而high逐步减少。如果high<low, 则查找失败,算法结束。
【示例】请给出在含有12个元素的有序表{1,4,10,16,17,18,23,29,33,40,50,51}中二分查找关健
字17的过程。
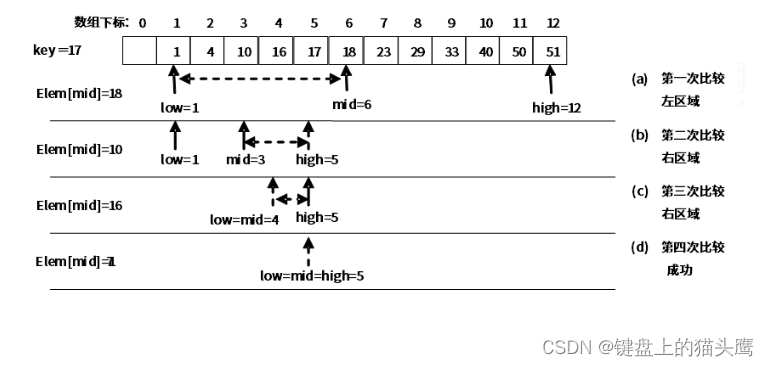
折半查找在查找成功时关键字的比较次数最多为+1次。
折半查找的时间复杂度为O()次。
折半查找的前提:有序、顺序存储。
考点3:哈希表查找
1.散列表
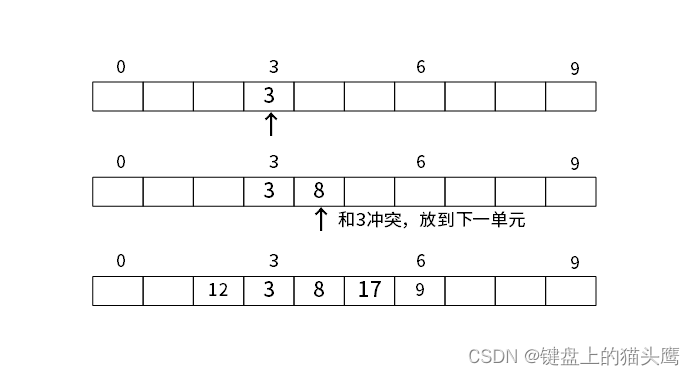
散列表查找的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关健
字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0...n-1]
(n<<m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
例:记录关键码为(3,8, 12, 17. 9) ,取m=10 (存储空间为1) ,p=5, 散列函数h=key%p。