1、单目运算符双目运算符
算数运算符分为单目运算符和双目运算符等
单目运算符只需要一个操作数,双目运算符需要两个操作数
- 双目运算符最常见:常见的算术运算符:±*/,比较运算符:<>=等等
- 以下是一些单目运算符:
正号 (+): 用于表示正数或给数值一个正号。例如:+5 仍然是 5。
num = +5
print(num) # 输出: 5
负号 (-): 用于表示负数或取一个数的相反数。例如:-5 是 -5,而 -(-5) 是 5。
num = -5
print(num) # 输出: -5
num = -(-5)
print(num) # 输出: 5
位非运算符 (~): 这是一个按位非运算符,用于对整数的每一位进行取反操作。例如,对于数字 5(其二进制表示为 101),位非运算的结果是 ~101,即 -6。
num = ~5
print(num) # 输出: -6
需要注意的是,Python中的大多数运算符(如加法、减法、乘法、除法、取模等)都是双目运算符,它们需要两个操作数。而逻辑运算符(如and、or、not)中的not是单目的,但它更常用于逻辑表达式中,而不是直接对单个值进行操作。
2、中缀表达式
两大特点:优先级、结合性
优先级:乘除法>加减法
结合性:优先计算括号内的表达式
中缀表达式交给计算机处理有很大的问题,计算机串行读数据,当遇到运算符时是立即计算还是延期计算
因此引入后缀表达式
3、后缀表达式
中缀表达式:3+4*(5+6)-3
后缀表达式:3456+*+3-
将中缀表达式转化成为后缀表达式有利于计算机处理算数运算
4、栈的应用——中缀转后缀
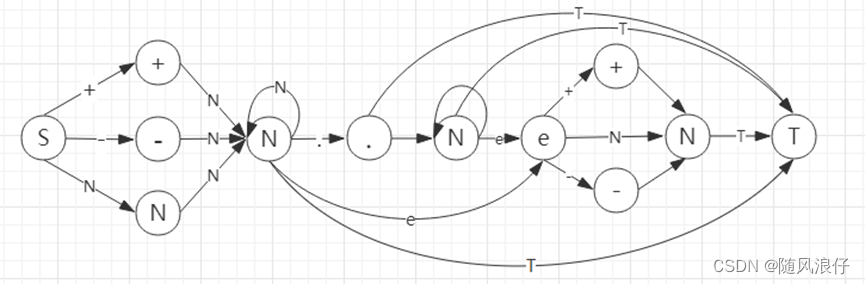
(1)手算图示

(2)计算机转化后缀表达式思路:
后缀表达式放在列表中,因为最后要将后缀表达式串行(按照顺序)读,运算符放在栈中,接下来解释过程
1、遇到数字:直接放在列表中
2、遇到符号分情况讨论
- 当栈为空:压入栈
- 当运算符优先级高于栈顶运算符:压入栈
- 遇到左括号,压入栈(括号相当与新的开始,括号后的符号优先级看作全部高于左括号)
- 遇到右括号,从栈中弹出运算符(append到后缀表达式列表中),直到遇到左括号
- 当运算符优先级低于或等于栈顶运算符,从栈中弹出运算符(append到后缀表达式列表中)
- 最后把栈中剩余的运算符弹出,直到栈为空
当然,要先把表达式利用正则表达式拆分,并利用字典定义符号优先级
(3)代码:
- 定义栈这样一个数据结构,具体方法如下:
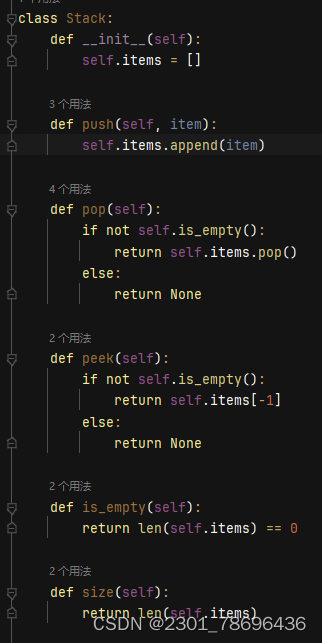
class Stack:
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
if not self.is_empty():
return self.items.pop()
else:
return None
def peek(self):
if not self.is_empty():
return self.items[-1]
else:
return None
def is_empty(self):
return len(self.items) == 0
def size(self):
return len(self.items)
- 用栈实现转化的代码:
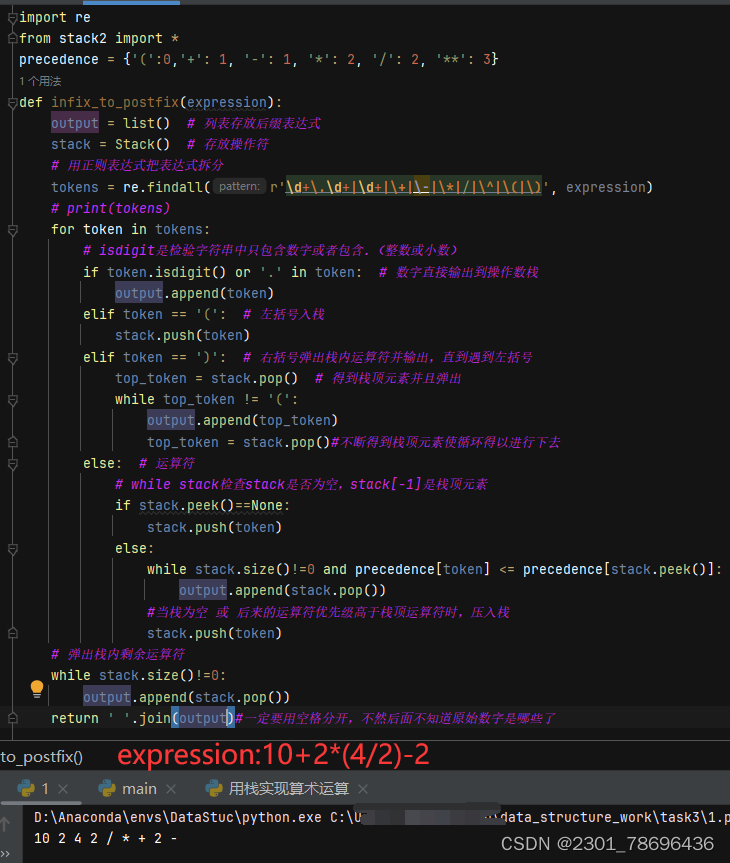
import re
from stack2 import *
precedence = {
'(':0,'+': 1, '-': 1, '*': 2, '/': 2, '**': 3}
def infix_to_postfix(expression):
output =