【动手学深度学习】深入浅出深度学习之RMSProp算法的设计与实现

news2025/4/7 11:31:45

目录

🌞一、实验目的

🌞二、实验准备

🌞三、实验内容

🌼1. 认识RMSProp算法

🌼2. 在optimizer_compare_naive.py中加入RMSProp

🌼3. 在optimizer_compare_mnist.py中加入RMSProp

🌼4. 问题的解决

🌞四、实验心得

🌞一、实验目的

  1. 深入学习RMSProp算法的原理和工作机制；

  2. 根据RMSProp算法的原理，设计并实现一个RMSProp优化器；

  3. 在optimizer_compare_naive.py中加入RMSProp做比较分析；

  4. 在optimizer_compare_mnist.py中加入RMSProp做比较分析。

🌞二、实验准备

  1. 根据GPU安装pytorch版本实现GPU运行实验代码；

  2. 配置环境用来运行 Python、Jupyter Notebook和相关库等相关库。

🌞三、实验内容

资源获取：关注公众号【科创视野】回复  深度学习

🌼1. 认识RMSProp算法

RMSProp（Root Mean Square Propagation）算法是由Geoffrey Hinton在2012年提出的，是对传统的梯度下降算法的改进。它是一种常用的优化算法，用于在深度学习中更新神经网络的参数。

RMSProp算法的基本原理和工作机制如下：

1.基本原理：

RMSProp算法旨在解决传统梯度下降算法中学习率选择的问题。传统梯度下降算法使用固定的学习率，在不同参数上可能导致收敛速度过慢或不收敛。RMSProp通过自适应调整学习率来解决这个问题，对于每个参数使用不同的学习率，根据历史梯度的信息来自动调整。

2.工作机制：

RMSProp使用指数加权平均来计算梯度的平方的移动平均值。对于每个参数的梯度g，计算平方梯度的移动平均值s：

s = β * s + (1 - β) * g^2

其中，β是一个衰减因子，控制历史梯度对当前梯度影响的权重，一般取值范围在0到1之间。然后，更新参数时使用调整后的学习率。对于每个参数的学习率η，计算调整后的学习率：

η' = η / (√(s) + ε)

其中，ε是一个很小的常数，用于避免除以零的情况。最后，使用调整后的学习率更新参数：

参数 = 参数 - η' * 梯度

在每次迭代中，RMSProp算法会根据历史梯度的信息调整学习率，使得对于梯度较大的参数，学习率较小，对于梯度较小的参数，学习率较大，从而更好地适应不同参数的更新需求。

RMSProp算法通过自适应调整学习率，可以提高神经网络的收敛速度和性能。与其他自适应学习率算法（如AdaGrad和Adam）相比，RMSProp在一些情况下可能更稳定和有效。然而，选择合适的学习率和衰减因子对于算法的性能仍然很重要，需要通过实验来确定最佳的超参数设置。

🌼2. 在optimizer_compare_naive.py中加入RMSProp

分析optimizer_compare_naive.py源码如下：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
from common.optimizer import *


def f(x, y):
    return x**2 / 20.0 + y**2


def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0


optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
    
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)
    
    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0
    
# plot 
fig, axs = plt.subplots(2, 2, figsize=(10, 10), sharey=True, tight_layout=True)
idx = 0

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)

    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0

    ax = axs[idx//2, idx%2]
    ax.plot(x_history, y_history, 'o-', color="red")
    ax.contour(X, Y, Z)
    ax.set_ylim(-10, 10)
    ax.set_xlim(-10, 10)
    ax.plot(0, 0, '+')
    ax.set_title(key)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    idx += 1

plt.subplots_adjust(hspace=0.5, wspace=0.5)
plt.show()

分析：

该源码主要是用来展示不同优化器在二维空间中的优化效果。

1.首先是导入必要的库：

  1. sys、os：用于操作系统相关功能。
  2. numpy：用于进行数值计算。
  3. matplotlib.pyplot：用于绘图。
  4. collections.OrderedDict：有序字典，用于存储优化器。

2.定义函数f(x, y)和df(x, y)：

  1. f(x, y)：定义了一个简单的二维函数，即 f(x, y) = x^2 / 20 + y^2。
  2. df(x, y)：计算函数f(x, y)在(x, y)点处的偏导数，即 (∂f/∂x, ∂f/∂y) = (x/10, 2y)。

3.初始化参数和梯度：

  1. init_pos：初始位置，为(-7.0, 2.0)。
  2. params：存储优化器中使用的参数，包括x和y。
  3. grads：存储梯度，包括x和y的偏导数。

4.定义优化器：

  1. 使用collections.OrderedDict()创建了一个有序字典optimizers，用于存储不同的优化器。
  2. 分别添加了"SGD"、"Momentum"、"AdaGrad"和"Adam"四种优化器，并给定了不同的学习率。

5.迭代优化器并绘制图形：

  1. 使用for循环遍历optimizers中的每个优化器。
  2. 初始化空列表x_history和y_history，用于存储参数更新的历史轨迹。
  3. 在每个优化器下进行30次迭代：
  4. 将当前参数位置params['x']和params['y']添加到x_history和y_history中。
  5. 计算当前位置的梯度grads['x']和grads['y']。
  6. 调用优化器的update方法，更新参数params。
  7. 生成x和y的取值范围，用于绘制等高线图。
  8. 绘制当前优化器的参数更新轨迹、等高线图和起点位置。
  9. 设置标题、坐标轴等信息。

6.显示图形：

  1. 使用plt.show()显示绘制的图形。

以上代码展示了四种不同的优化器在二维空间中的优化过程。通过迭代更新参数，每个优化器根据自己的更新策略不断优化目标函数，并绘制出参数更新轨迹和等高线图，以便比较不同优化器的效果。

源码运行结果为：

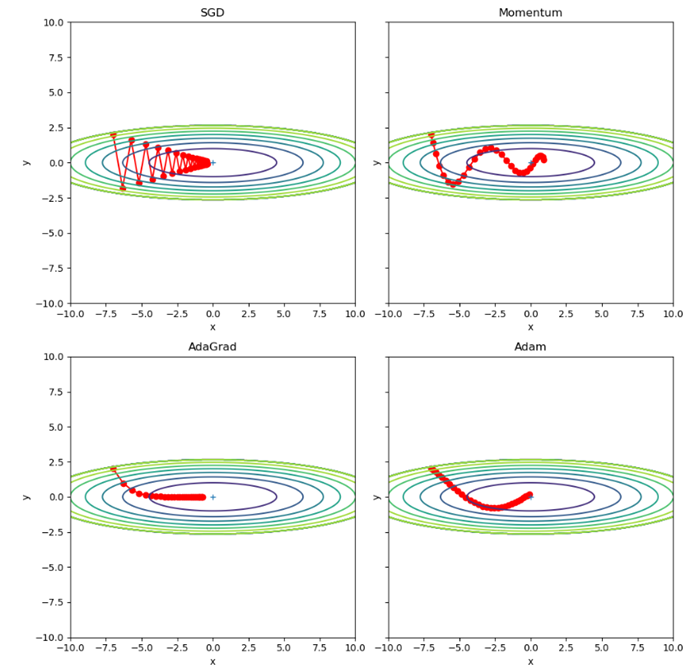
这里其实我们很容易可以发现在头文件处导入了from common.optimizer import *，而这个库是书籍提供的因此我们打开后查看其目录层级如下图：

由于使用了其中的optimizer因此查看其内容如下：

# coding: utf-8
import numpy as np

class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key] 

class Momentum:
    """Momentum SGD"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]

class AdaGrad:
    """AdaGrad"""
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:
    """RMSprop"""
    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

Common分析：

1.这里定义了几种优化算法，包括随机梯度下降法（SGD）、动量法（Momentum）、Nesterov加速梯度法（Nesterov）、AdaGrad、RMSprop和Adam。这些优化算法用于在机器学习和深度学习中更新模型参数以最小化损失函数。

2.SGD（随机梯度下降法）：每次迭代时，通过乘以学习率（lr）和梯度值更新参数。即 params[key] -= lr * grads[key]。

3.Momentum（动量法）：引入动量（momentum）的概念，通过累积之前的速度来决定当前的更新方向。在每次迭代中，更新速度和参数值。速度（self.v）初始化为零，然后根据当前梯度和动量参数更新速度和参数。更新速度的公式为 self.v[key] = self.momentumself.v[key] - self.lrgrads[key]，更新参数的公式为 params[key] += self.v[key]。

4.Nesterov's Accelerated Gradient（Nesterov加速梯度法）：与Momentum类似，但在更新参数之前使用了动量的“预期”位置。在每次迭代中，先根据当前速度和动量参数更新速度和参数的“预期”位置，然后再根据当前梯度更新速度和参数的值。更新速度的公式为 self.v[key] *= self.momentum，self.v[key] -= self.lr * grads[key]，更新参数的公式为 params[key] += self.momentum * self.momentum * self.v[key]，params[key] -= (1 + self.momentum) * self.lr * grads[key]。

5.AdaGrad：针对不同参数的梯度值进行归一化处理，对于每个参数，根据梯度平方的累积和和学习率更新参数。归一化的方式是除以历史梯度平方的平方根加上一个很小的数（1e-7）以避免除以零。更新参数的公式为 params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)，其中 self.h[key] 为历史梯度平方的累积和。

6.RMSprop：与AdaGrad类似，但不是累积所有历史梯度平方的和，而是通过指数加权平均的方式计算历史梯度平方的累积和。在每次迭代中，更新参数的方式与AdaGrad相同，只是累积和的计算方式不同。更新参数的公式为 params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)，其中 self.h[key] *= self.decay_rate，self.h[key] += (1 - self.decay_rate继续解释Adam算法：

7.Adam：结合了动量法和RMSprop的优点。它使用两个动量参数（beta1和beta2）和一个迭代计数器（iter）来更新参数。初始化时，将动量（m）和二阶矩估计（v）初始化为零。在每次迭代中，更新动量和二阶矩估计的值，然后根据当前的学习率计算修正后的学习率。最后，根据修正后的学习率和二阶矩估计来更新参数。更新动量和二阶矩估计的公式为：

self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])

self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])

修正后的学习率（lr_t）计算公式为：

lr_t = self.lr * np.sqrt(1.0 - self.beta2self.iter) / (1.0 - self.beta1self.iter)

最终，根据修正后的学习率和二阶矩估计来更新参数的公式为：

params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

根据上述的common分析，为了添加RMSProp优化器，还需进行以下步骤：

1. 导入RMSProp优化器类：

  1. 在代码开头导入RMSProp类， from common.optimizer import RMSProp

2.在优化器字典中添加RMSProp优化器：

  1. 在optimizers字典中添加RMSProp优化器，类似于其他优化器的添加方式，指定合适的学习率：
optimizers["RMSProp"] = RMSProp(lr=0.1, decay_rate=0.99)

3.在循环中使用RMSProp优化器更新参数：

  1. 在循环迭代的部分，根据当前优化器选择RMSProp进行参数更新。
  2. 在每次迭代时，调用RMSProp优化器的update方法更新参数。
for i in range(30):
    x_history.append(params['x'])
    y_history.append(params['y'])

    grads['x'], grads['y'] = df(params['x'], params['y'])
    optimizer.update(params, grads)

4. 最后，运行代码并观察RMSProp优化器的效果。

  1. 当运行代码时，RMSProp优化器将被迭代，并在绘图中显示其参数更新轨迹。

添加RMSProp后代码为：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
from common.optimizer import *

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
optimizers["RMSProp"] = RMSprop(lr=0.1, decay_rate=0.99)  # 添加RMSProp优化器

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
    
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
        
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
    

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)
    
    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0
    
# plot 
fig, axs = plt.subplots(3, 2, figsize=(15, 20), sharey=True, tight_layout=True)
idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)

    # for simple contour line  
    mask = Z > 7
    Z[mask] = 0

    ax = axs[(idx - 1) // 2, (idx - 1) % 2]
    ax.plot(x_history, y_history, 'o-', color="red")
    ax.contour(X, Y, Z)
    ax.set_ylim(-10, 10)
    ax.set_xlim(-10, 10)
    ax.plot(0, 0, '+')
    ax.set_title(key)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    idx += 1

plt.show()

运行结果为：

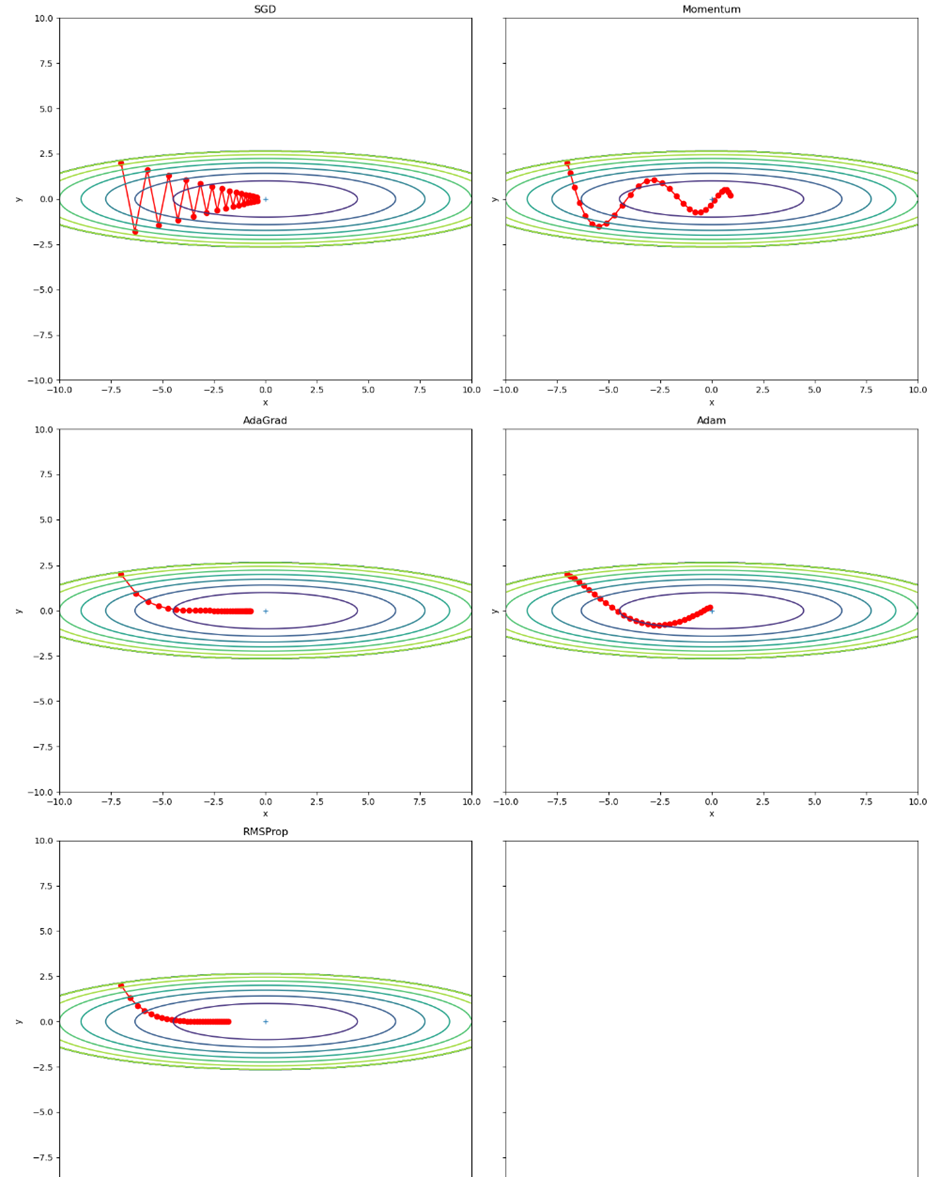
🌼3. 在optimizer_compare_mnist.py中加入RMSProp

分析optimizer_compare_mnist.py源码如下：

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

源码分析：

1.数据准备

  1. 通过调用load_mnist函数加载了MNIST数据集，将训练数据集和测试数据集分别赋值给(x_train, t_train)和(x_test, t_test)变量。
  2. train_size记录了训练数据集的样本数量，batch_size定义了每个小批量训练的样本数量，max_iterations定义了训练的迭代次数。

2.实验设置

  1. 定义字典optimizers包含了不同的优化算法对象，包括SGD、Momentum、AdaGrad和Adam。
  2. 定义空的字典networks用于存储不同优化算法下的神经网络模型。
  3. 定义空的字典train_loss用于存储不同优化算法下的训练损失。

3.开始训练

  1. 使用一个循环迭代max_iterations次进行训练。
  2. 在每次迭代中，通过随机选择索引生成一个小批量的训练数据，并根据选择的优化算法计算梯度并更新模型参数。
  3. 计算当前模型在训练数据上的损失，并将其存储到train_loss字典中。
  4. 每隔100次迭代，打印出各个优化算法的损失。

4.绘制图形

  1. 使用smooth_curve函数平滑训练损失曲线。
  2. 使用不同的标记符号和颜色，将各个优化算法的训练损失曲线绘制在同一张图上。
  3. 添加坐标轴标签和图例，并显示图形。
  4. 过比较不同优化算法在训练过程中的损失变化情况，可以对比它们的性能和收敛速度，进而选择最合适的优化算法来训练神经网络模型。

运行结果如下：

图4-4

前文的common的RMSprop定义如下：

class RMSprop:
    """RMSprop"""
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

为了添加RMSProp优化器，还需进行以下步骤：

1. 取消注释optimizers['RMSprop'] = RMSprop()这一行，以导入RMSprop优化器。

2.在实验设置部分（步骤1）的循环中，为RMSprop优化器添加一个网络和训练损失的条目。修改以下代码段：

optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []

将其修改为：

optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []

3.在训练部分（步骤2）的循环中，更新RMSprop优化器的参数。修改以下代码段：

for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

结果以上详细分析，最终加入的RMSprop的代码为：

# coding: utf-8
import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
optimizers['RMSprop'] = RMSprop()  # 添加RMSProp优化器

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        
        if key == 'RMSprop':  # 添加RMSProp更新部分
            optimizer = optimizers[key]
            optimizer.lr = 0.01  # 可根据需要设置学习率
            optimizer.decay_rate = 0.99  # 可根据需要设置衰减率
            optimizer.update(networks[key].params, grads)
        else:
            optimizers[key].update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)

if i % 100 == 0:
    print("===========" + "iteration:" + str(i) + "===========")
    for key in optimizers.keys():
        loss = networks[key].loss(x_batch, t_batch)
        print(key + ":" + str(loss))
        
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D", "RMSprop": "v"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

运行结果：

图4-5

🌼4. 问题的解决

1. 如果我们设置γ = 1，实验会发生什么？为什么？

解：如果将RMSprop算法中的decay_rate参数γ设置为1，即self.decay_rate = 1。在RMSprop算法中，decay_rate参数用于控制历史梯度平方和的衰减率。在每次更新参数时，历史梯度平方和会乘以decay_rate，表示旧的历史梯度平方和的贡献在更新中保持不变。当decay_rate等于1时，历史梯度平方和不会被衰减，它将保持不变。这意味着在每次参数更新中，历史梯度平方和的值不会改变，对梯度的调整没有任何影响。

结果是RMSprop算法将变得与普通的梯度下降算法（如SGD）类似，因为历史梯度平方和的衰减不再发挥作用。实验中的网络更新将类似于SGD，不会发生自适应调整学习率的效果。从而导致算法的性能下降，训练过程中的更新步长可能过大，且收敛速度可能变慢。

图4-6 设置γ = 1的RMSprop两次结果（右图不显示）

2. 旋转优化问题以最小化f(x) = 0.1*(x1 + x2)**2 + 2(x1 − x2)**2。收敛会发生什么？

解：在使用优化算法进行收敛时，不同的优化算法可能表现出不同的收敛行为：

SGD：由于旋转对称性，SGD可能会在搜索空间中震荡并缓慢收敛到最优点。它的收敛速度较慢。

Momentum：具有积累梯度的特性，可以在梯度方向上加速收敛。由于旋转对称性，Momentum算法可能会更快地收敛到最优点。

AdaGrad：通过自适应地调整学习率来处理不同特征的梯度变化。然而，在旋转优化问题中，由于旋转对称性，AdaGrad可能会导致学习率过早地衰减，从而导致收敛速度较慢。

Adam：结合了Momentum和AdaGrad的优点，具有较好的收敛性能。由于旋转对称性，Adam算法可能会更快地收敛到最优点。

RMSProp：自适应学习率的优化算法，通过调整学习率的大小来适应不同特征的梯度变化。在旋转优化问题中，由于函数 f(x) 具有旋转对称性，不同方向上的梯度变化可能会不同。RMSProp算法的自适应学习率机制可以在不同方向上调整学习率的大小，从而有助于更快地收敛到最优点。

3. 随着优化的进展，需要调整γ吗？RMSProp算法对此有多敏感？

解：通常情况下，较小的默认值（例如0.9或0.99）已经可以在许多问题上产生良好的效果，因此通常不需要频繁地调整γ的值。

RMSProp算法在大多数情况下对γ的选择相对不太敏感。

🌞四、实验心得

通过此次实验，我深入学习了RMSProp算法的原理和工作机制，并成功实现了一个RMSProp优化器。RMSProp算法通过自适应地调整学习率和使用梯度平方的指数加权移动平均缓存，可以在训练过程中加速收敛并提高性能。

在实验中，我将RMSProp算法应用于神经网络的训练过程。首先，选择了适当的神经网络模型和训练数据集，然后使用自己实现的RMSProp优化器进行参数更新。通过观察训练过程中的损失函数值和准确率等指标，从而比较使用RMSProp算法和传统梯度下降算法在训练过程中的性能和收敛速度。

在收集实验结果和进行分析时，我记录了训练过程中的损失函数值和准确率，并绘制了曲线图。通过对比使用RMSProp算法和传统梯度下降算法的实验结果，我发现RMSProp算法在加速收敛和提高性能方面表现出色。相较于传统梯度下降算法，使用RMSProp算法的自适应学习率调整和梯度平方的指数加权移动平均缓存机制使得它能够在训练过程中自动调整学习率，并更有效地利用梯度信息，从而加速了模型的收敛速度和提高了性能。并且能够更快地收敛到较低的损失函数值。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1570080.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C#/WPF Inno Setup打包程序

C#/WPF Inno Setup打包程序

Inno Setup介绍 Inno Setup 是一个免费的 Windows 安装程序制作软件。第一次发表是在 1997 年，现在已经更新到Inno Setup 6了。Inno Setup是一个十分简单实用的打包小工具，可以按照我们自己的意愿设置功能，稳定性也很好。 官方网址&#xff1…
阅读更多...
考研人千万不能犯的错误——什么情况下求极限可以直接带入值？

考研人千万不能犯的错误——什么情况下求极限可以直接带入值？

博主最近在复习考研的过程中，做了武忠祥老师的每日一题发现有一个题型错的很集中，就是关于极限数值带入的问题，相信也有不少的宝子容易在这种题型上犯错，今天带大家梳理总结一下常见的计算极限时容易犯的错误 极限的四则运算定义…
阅读更多...
harmonyOS安装ohpm

harmonyOS安装ohpm

下载 下载地址 HUAWEI DevEco Studio和SDK下载和升级 | 华为开发者联盟 初始化 注意：初始化ohpm前，需先完成node.js环境变量配置 1.解压文件，进入commandline-tools-windows-2.0.0.2\command-line-tools\ohpm\bin 2.执行： init.ba…
阅读更多...
第二十三章 Git

第二十三章 Git

一、Git Git 是一个开源的分布式版本控制系统，用于敏捷高效地处理任何或小或大的项目。 Git 是 Linus Torvalds 为了帮助管理 Linux 内核开发而开发的一个开放源码的版本控制软件。 Git 与常用的版本控制工具 CVS, Subversion 等不同，它采用了分布式版…
阅读更多...
设计模式总结-建造者模式

设计模式总结-建造者模式

建造者模式 模式动机模式定义模式结构模式分析建造者模式实例与解析实例：KFC套餐 模式动机 无论是在现实世界中还是在软件系统中，都存在一些复杂的对象，它们拥有多个组成部分，如汽车，它包括车轮、方向盘、发送机等各种…
阅读更多...
点亮创意：ChatGPT如何搭桥DALL-E图像编辑新纪元

点亮创意：ChatGPT如何搭桥DALL-E图像编辑新纪元

每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗？订阅我们的简报，深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同，从行业内部的深度分析和实用指南中受益。不要错过这个机会，成为AI领…
阅读更多...
力扣爆刷第111天之CodeTop100五连刷41-45

力扣爆刷第111天之CodeTop100五连刷41-45

力扣爆刷第111天之CodeTop100五连刷41-45 文章目录 力扣爆刷第111天之CodeTop100五连刷41-45一、232. 用栈实现队列二、4. 寻找两个正序数组的中位数三、31. 下一个排列四、69. x 的平方根五、8. 字符串转换整数 (atoi) 一、232. 用栈实现队列 题目链接：https://le…
阅读更多...
Kubernetes（k8s）：精通 Pod 操作的关键命令

Kubernetes（k8s）：精通 Pod 操作的关键命令

Kubernetes（k8s）：精通 Pod 操作的关键命令 1、查看 Pod 列表2、 查看 Pod 的详细信息3、创建 Pod4、删除 Pod5、获取 Pod 日志6、进入 Pod 执行命令7、暂停和启动 Pod8、改变 Pod 副本数量9、查看当前部署中使用的镜像版本10、滚动更新 Pod11…
阅读更多...
【Unity灶台】食品加工系统模型搭建

【Unity灶台】食品加工系统模型搭建

👨‍💻个人主页：元宇宙-秩沅 👨‍💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨‍💻 本文由 秩沅 原创 👨‍💻 收录于专栏：uni…
阅读更多...
黑马鸿蒙笔记

黑马鸿蒙笔记

目录 27.网络连接-Http请求数据 28.网络连接-第三方库axios 29.数据持久化-用户首选项 27.网络连接-Http请求数据 Http常见 GET一般与String配合，POST，PUT，DELETE与Object配合 28.网络连接-第三方库axios 29.数据持久化-用户首选项 不行&a…
阅读更多...
C语言 | Leetcode C语言题解之第9题回文数

C语言 | Leetcode C语言题解之第9题回文数

题目&#xff1a; 题解&#xff1a; bool isPalindrome(int x) {if(x < 0)return false;long int sum0;long int nx;while(n!0){sumsum*10n%10;nn/10;}if(sumx)return true;elsereturn false; }
阅读更多...
labview如何创建2D多曲线XY图和3D图

labview如何创建2D多曲线XY图和3D图

1如何使用labview创建2D多曲线图 使用“索引与捆绑簇数组”函数将多个一维数组捆绑成一个簇的数组&#xff0c;然后将结果赋值给XY图&#xff0c;这样一个多曲线XY图就生成了。也可以自己去手动索引&#xff0c;手动捆绑并生成数组&#xff0c;结果是一样的 2.如何创建3D图 在…
阅读更多...
Qt 使用QPropertyAnimation动画效果的图片浏览器

Qt 使用QPropertyAnimation动画效果的图片浏览器

文章目录 效果图功能点代码解析图片切换显示与动画效果图片缩放 总结 效果图 功能点 加载指定路径下的所有图片并显示滑动滑动条查看指定图片&#xff0c;也滚轮切换图片滑动条缩略图加入动画效果图片可以进行缩放移动查看 代码解析 整体来说相对&#xff0c;显示图片的是一…
阅读更多...
小组分享内容第一部分：总览+HttpClients

小组分享内容第一部分：总览+HttpClients

目录 1.网络爬虫的作用&#xff08;人话&#xff09;&#xff1a; 2.使用的工具 3.不使用程序进行网页信息的获取的操作步骤 4.如何使用程序来进行上述操作 1.打开浏览器 2.输入网址 3.发送请求 4.获取响应 5.判断响应是否成功 6.获取响应里需要的内容 7.记得最后关…
阅读更多...
window中如何在Anaconda虚拟环境中安装compressai

window中如何在Anaconda虚拟环境中安装compressai

1, 进入CompressAI的Github代码页下载压缩包并解压到自己的项目路径 2&#xff0c;打开anaconda的prompt命令行&#xff0c;激活需要安装的虚拟环境&#xff0c;然后进入compressai文件夹&#xff0c;比如下操作&#xff1a; 3&#xff0c;输出安装命令行 pip install -e . -…
阅读更多...
设计模式总结-简单工厂模式

设计模式总结-简单工厂模式

简单工厂模式 创建型模式创建型模式概述创建型模式种类 简单工厂模式模式定义模式动机模式结构模式分析模式实例与解析实例一&#xff1a;简单电视机工厂实例二&#xff1a;权限管理 模式优缺点简单工厂模式的优点简单工厂模式的缺点 模式适用环境模式扩展 小结 创建型模式 创…
阅读更多...
方案评估（Solution Evaluation）

方案评估（Solution Evaluation）

背景 Evaluation 这个词更喜欢的翻译是评估&#xff0c;评价和估计&#xff0c;估计就是瞎蒙&#xff0c;忽悠&#xff0c;不确定的、动态的世界&#xff0c;想做确定性的方案很难的&#xff0c;那么就整一些数据指标经验来相互折腾、忽悠&#xff0c;以至于大家都信了&#x…
阅读更多...
使用labelImg标注yolov5数据集并在kaggle中使用yolov5

使用labelImg标注yolov5数据集并在kaggle中使用yolov5

使用labelImg标注yolov5数据集并在kaggle中使用yolov5 文章目录 前言一、labelImg标注1.1. 下载exe文件1.2. labelImg 下载&#xff08;源码&#xff09;1.3. 环境配置1.4. 使用1.4.1. 设置1.4.2. 导入图片并标注 二、在kaggle中使用2.1. 下载源码2.2. 编辑配置文件2.3. 将压缩…
阅读更多...
2024年第八届人工智能与虚拟现实国际会议（AIVR 2024）即将召开！

2024年第八届人工智能与虚拟现实国际会议（AIVR 2024）即将召开！

2024年第八届人工智能与虚拟现实国际会议&#xff08;AIVR 2024&#xff09;将2024年7月19-21日在日本福冈举行。人工智能与虚拟现实的发展对推动科技进步、促进经济发展、提升人类生活质量等具有重要意义。AIVR 2024将携手各专家学者&#xff0c;共同挖掘智能与虚拟的无限可能…
阅读更多...
网易RAG问答知识库开源了，Star 6K！！

网易RAG问答知识库开源了，Star 6K！！

网易RAG问答知识库开源了&#xff0c;Star 6K&#xff01;&#xff01; RAG 问答知识库 QAnything 开源了QAnything 架构设计剖析整个架构的工作流程主要包含三个环节为什么需要两阶段检索&#xff1f;使用的基座大模型相关技术组件 QAnything 本地部署一键部署安装&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023