保研线性代数复习3

news2025/6/30 8:52:33

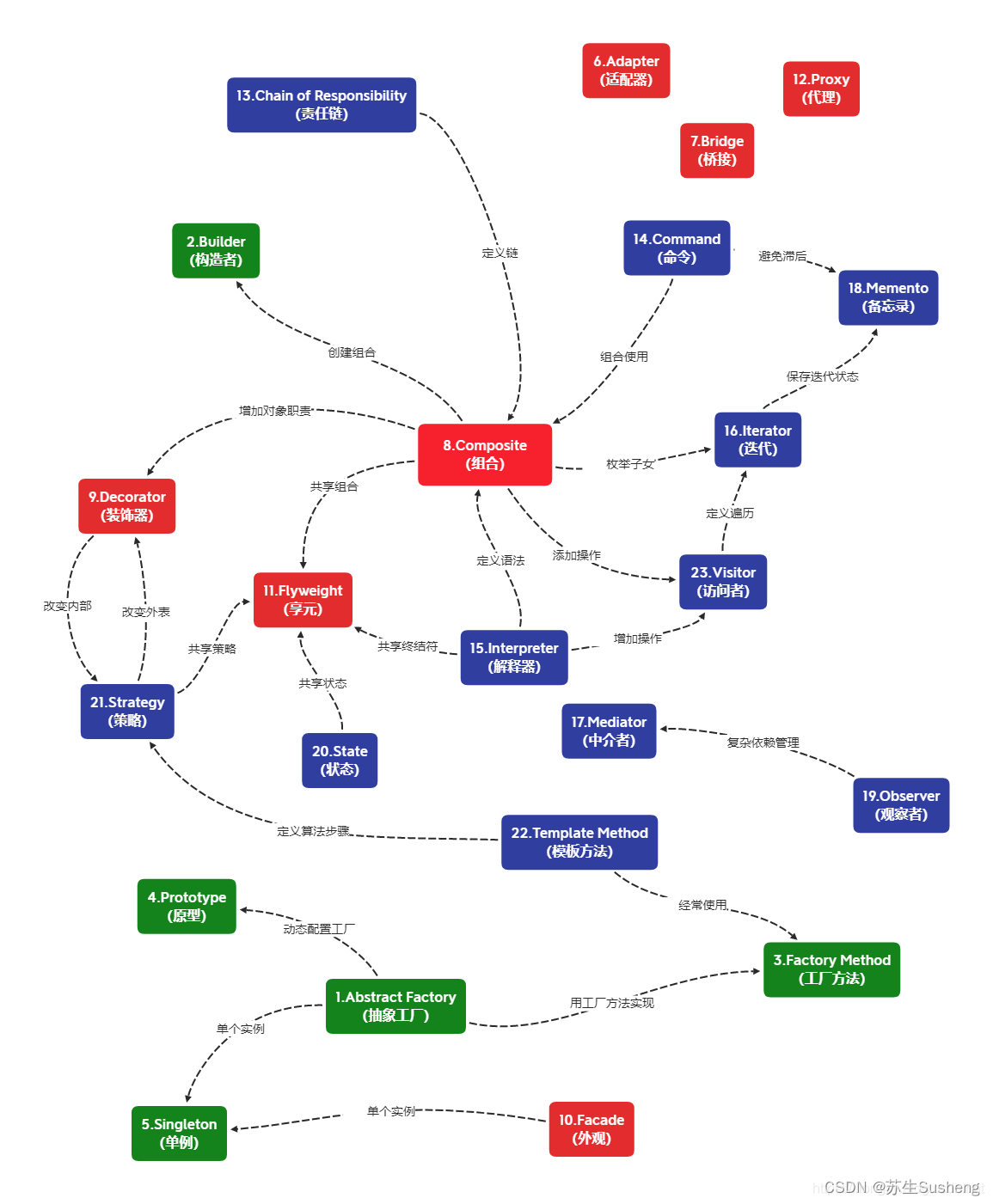
一.基底（Basis）

1.什么是生成集（Generating Set）？什么是张成空间（Span）？

存在向量空间V=(V，+，*)，和向量集 $A=\left \{ x_1,...,x_k \right \}\subseteq V$ （xi是所说的列向量），如果每一个属于V的向量都能被A中向量线性组合来表示，那么说明 A 是向量空间 V 的生成集，A的所有线性组合（所有线性组合不同）称为A的张成空间。

如果A张成了线性空间V，写成V=span[A]=span[x1,...,xk]。

2.什么是基底（Basis）？

基底是相对于向量空间来说的，每一个向量空间都拥有一个基底。例如向量空间V，向量空间V的基底B是向量空间V最小的（除了B之外没有B的子集可以张成向量空间V）线性无关的生成集。对于基底B，增加任何其他向量到B中都会让这个向量集合线性相关，所以基底B也称作向量空间V中最大线性无关的集合。

举例： $R^3$ 的标准基是（当然不止下面这几个）

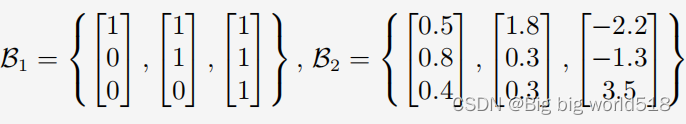
3.如何定义向量空间的维数（dimension）？

对于一个确定的向量空间V，向量空间V的基底中基向量（列向量）的个数是相同的。并且基底中基向量的个数等于向量空间的维数。

4.给定一个矩阵A（n个列向量），A是向量空间V的子集，如何找到A张成的向量空间的基底？

根据行阶梯法找到A中线性无关的向量组合。

二.秩（Rank）

1.什么是矩阵A的秩rk(A)？

矩阵 $A\epsilon R^{m*n}$ ，矩阵A线性无关的行向量的个数=矩阵A线性无关的列向量的个数=rk(A)。

2.矩阵的秩的性质如下：

矩阵A的秩=矩阵A的转置的秩

矩阵 $A\epsilon R^{m*n}$ 的列向量张成一个子空间 $U\epsilon R^m$ ，dim(U)=rk(A)

如果矩阵 $A\epsilon R^{m*n}$ 是正则的/可逆的，那么rk(A)=n

线性方程组 $Ax=b$ 有解的条件是rk(A)=rk(A|b)

对于 $A\epsilon R^{m*n}$ ， $Ax=0$ 的解的维数是n-rk(A)

如果 $A\epsilon R^{m*n}$ 满秩，那么rk(A)=min(m,n)

三.线性映射（Linear Mapping）

1.什么是线性映射？

对于向量空间V和W，存在一种映射 $\Phi:V\rightarrow W$ 称为线性映射并且要满足下面的条件：。

2.什么是单射双射满射？

单射满射双射都是基于线性映射，满足不同的情况的时候线性映射称为单射满射双射。

单射（injective）:原域中的样本对应目标域中的不同元素。

满射（surjective）:原域中至少存在一个目标域对应元素，原域中的样本就应该把目标域中的样本对应满。

双射（bijective）：单射和满射

3.什么是同构（Isomorpshism）？什么是自同态（Endomorphism）？什么是自同构（Automorphism）？

同构：线性映射and双射，两个有限维度的向量空间同构说明他们的维度相同。如果 $\Phi$ 是同构的，那么 $\Phi ^{-1}$ 也是同构的。

自同态： $\Phi: V\rightarrow V$ ，线性

自同构： $\Phi: V\rightarrow V$ ，线性and双射

4.什么是坐标（coordinate）？

对于一个线性空间V，和向量空间V的有序基底B=(b1,...bn)，对于任何一个 $x\in V$ ，我们都能得到一个唯一的线性组合 $x=\alpha_1b_1+...+\alpha_nb_n$ ，这些α1...αn称为是向量x相对于基底B的坐标。如果基底B不同，那么表示一个向量x的坐标不同。