| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 1. 倒退+迭代(除基取余法)
- 2. 省略掉反转操作
- 3. 系统提供API的自实现
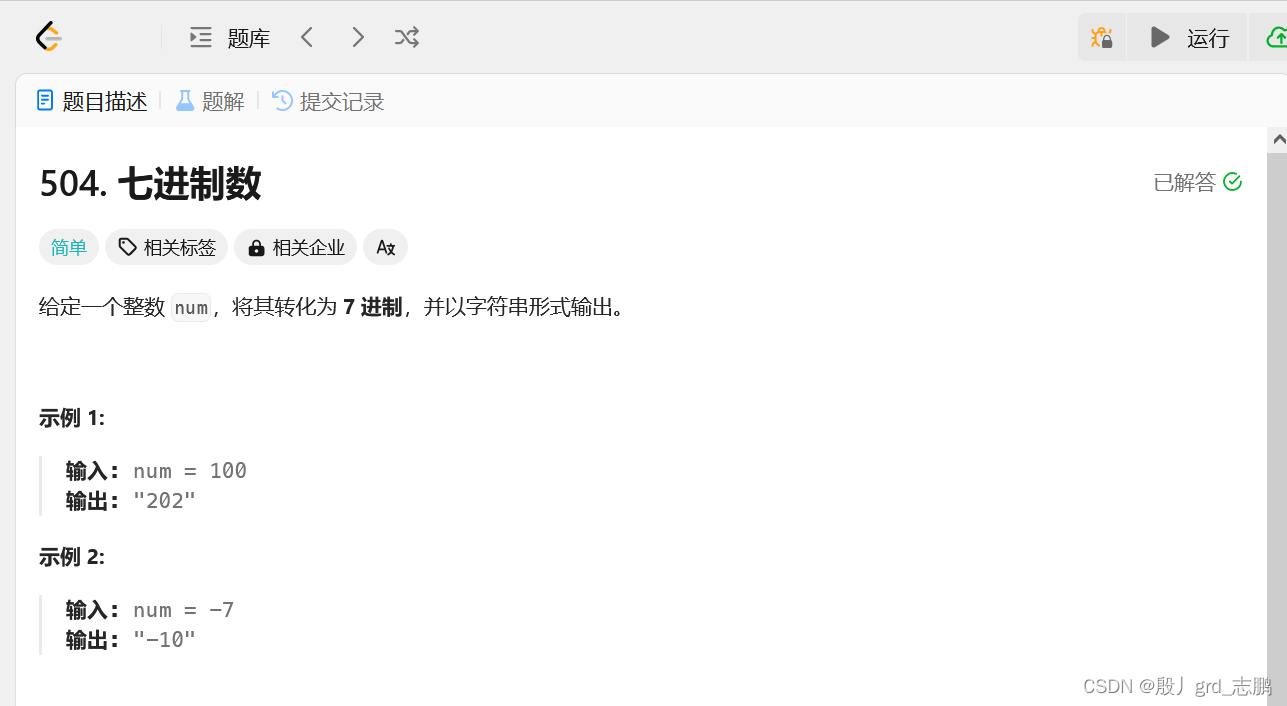
当使用经典算法除基取余法后,发现效率最快的是调用的系统提供的API,所以我研究了底层代码,会在方法二给出。法一依然是经典的除基取余法。
1. 倒退+迭代(除基取余法)
| 解题思路:时间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣),空间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣) |
|---|
- 如果是0,则不需要转换,直接返回0
- 创建一个negative的boolean型变量,如果num是负数,就设置为true
- 然后num取绝对值,我们只对正数操作
- 我们通过字符数组,来保存除基取余的结果
- 每次都将取余7的结果保存到数组中,然后num变为除以7的商。就是除基取余的原理。直到num被除完。
- 最后如果negative是true,就添加一个负号
- 因为除基取余法,需要从后往前读取结果,所以需要我们将数组反转后返回
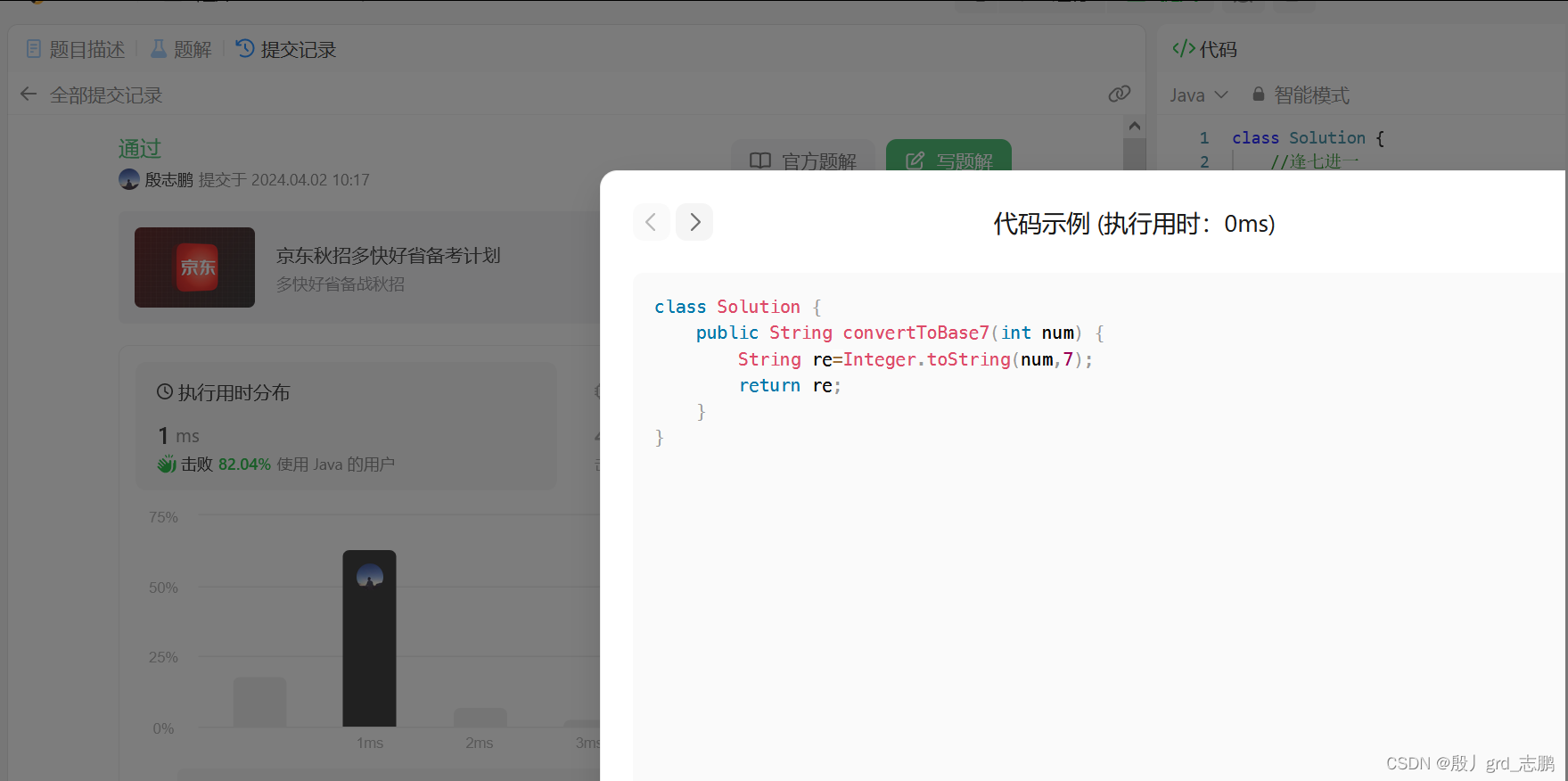
class Solution {
public String convertToBase7(int num) {
if (num == 0) return "0";
boolean negative = num < 0;
num = Math.abs(num);
StringBuffer digits = new StringBuffer();
while (num > 0) {
digits.append(num % 7);
num /= 7;
}
if (negative) {
digits.append('-');
}
return digits.reverse().toString();
}
}
2. 省略掉反转操作
| 解题思路:时间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣),空间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣) |
|---|
- 法一中,我们最后需要将整个结果进行反转操作,因为这是除基取余的特性
- 但是如果我们从一开始就反着添加结果,最后不就不需要反转了吗?
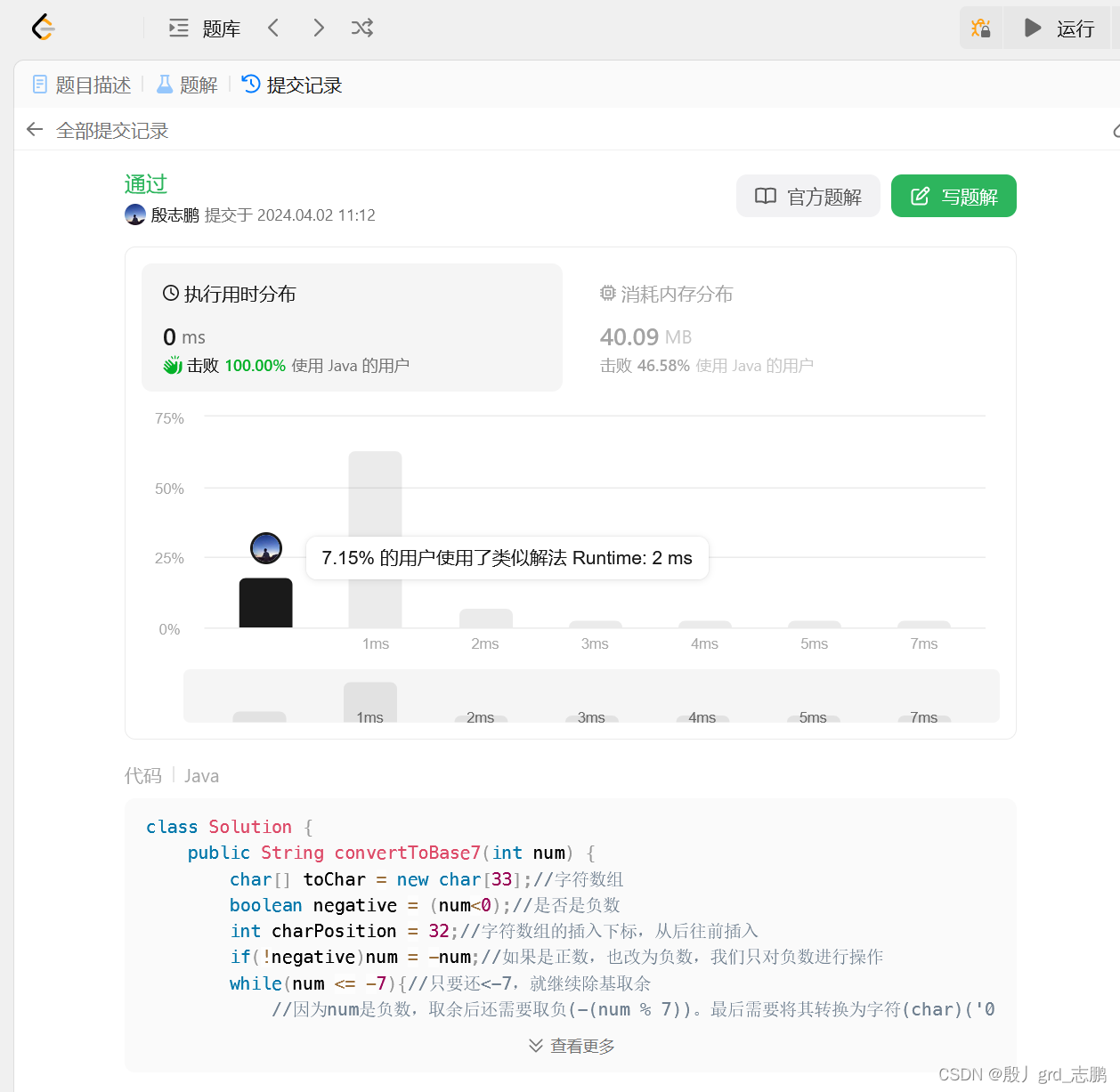
class Solution {
public String convertToBase7(int num) {
char[] toChar = new char[33];
boolean negative = (num<0);
int charPosition = 32;
if(!negative)num = -num;
while(num <= -7){
toChar[charPosition--] = (char)('0'+(-(num % 7)));
num = num/7;
}
toChar[charPosition] = (char) ('0'+(-num));
if(negative)toChar[--charPosition] = '-';
String s = new String(Arrays.copyOfRange(toChar, charPosition, charPosition+(33 - charPosition)));
return s;
}
}
3. 系统提供API的自实现
| 解题思路:时间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣),空间复杂度O(
l
o
g
2
∣
n
u
m
∣
log_2|num|
log2∣num∣) |
|---|
- Java提供的API是通过字节数组实现,效率更高
- 我们也通过字节数组将其实现. 而其实现居然和我们法二中大差不差,而且也是省略了反转操作。居然和我优化后的思路是一样的。
| 代码:效率会比法二高很多,但是官方测试用例太小,已经无法体现出差距了,如果数据量够大,一定是这个方法的字节数组更快。 |
|---|
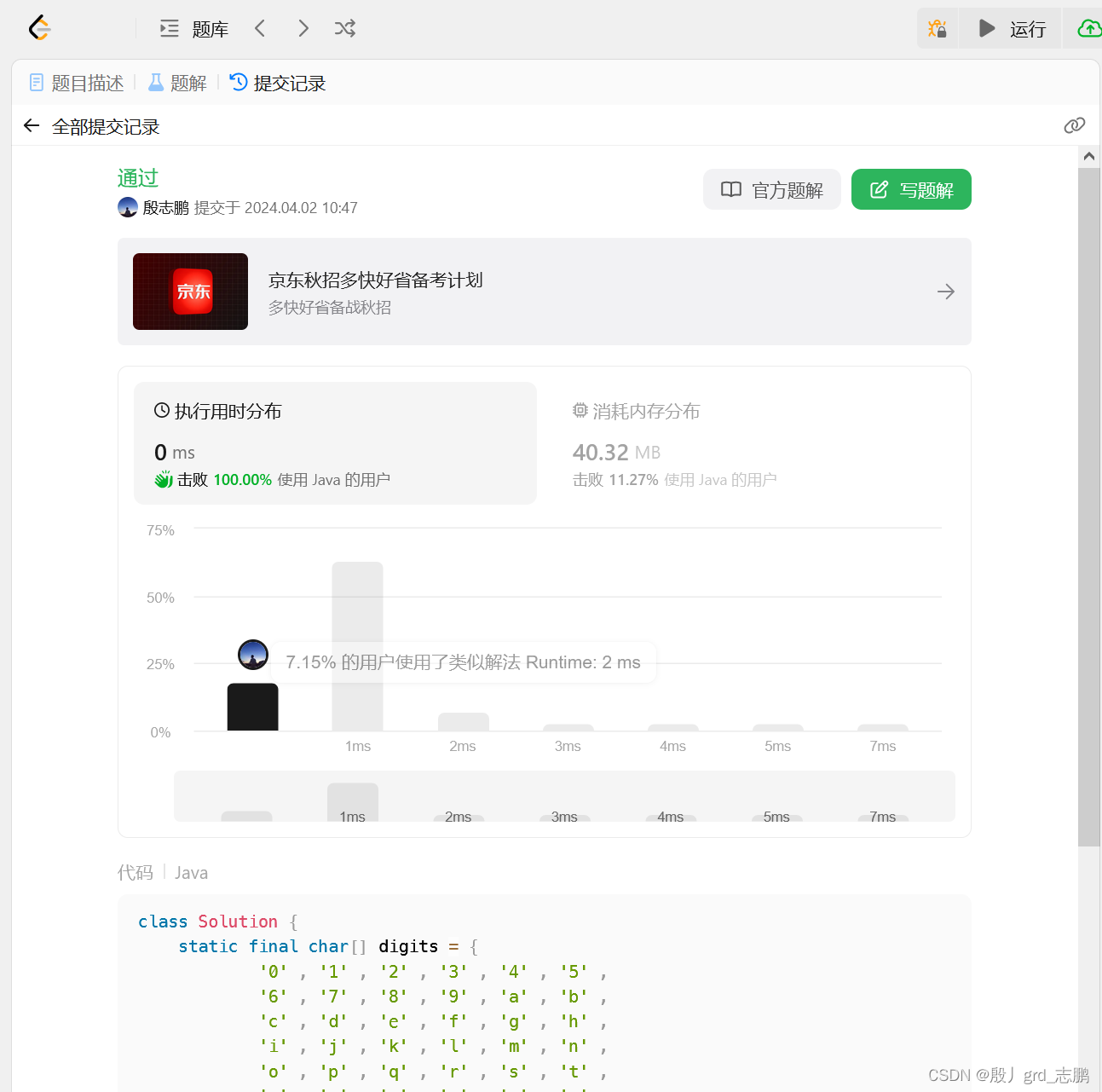
class Solution {
static final char[] digits = {
'0' , '1' , '2' , '3' , '4' , '5' ,
'6' , '7' , '8' , '9' , 'a' , 'b' ,
'c' , 'd' , 'e' , 'f' , 'g' , 'h' ,
'i' , 'j' , 'k' , 'l' , 'm' , 'n' ,
'o' , 'p' , 'q' , 'r' , 's' , 't' ,
'u' , 'v' , 'w' , 'x' , 'y' , 'z'
};
public String convertToBase7(int num) {
byte[] buf = new byte[33];
boolean negative = (num<0);
int charPosition = 32;
if(!negative)num = -num;
while(num <= -7){
buf[charPosition--] = (byte)digits[-(num % 7)];
num = num/7;
}
buf[charPosition] = (byte) digits[-num];
if(negative)buf[--charPosition] = '-';
String s = new String(Arrays.copyOfRange(buf, charPosition, charPosition+(33 - charPosition)));
return s;
}
}











![[计算机知识] 各种小问题思考](https://img-blog.csdnimg.cn/direct/9e0d7351c3c9427291ebd7b73c2be0f4.png)