题目

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

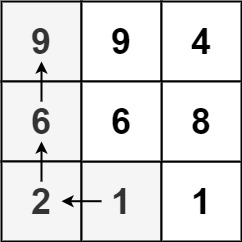
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

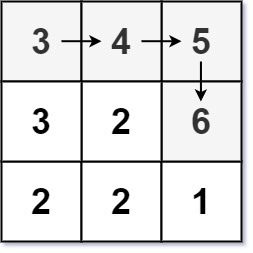
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

注意：本题与主站 329 题相同： . - 力扣（LeetCode）

---

请问您在哪类招聘中遇到此题？

1/5

社招

校招

实习

未遇到

通过次数

16.3K

提交次数

28.2K

通过率

57.6%

记忆化搜索

遍历所有的点[i][j]，求出从[i][j]为起点时的递增路径长度，所有长度的最大值即为所求。正常搜索时会有很多重复操作，所以加上一个记忆化的数组f来记录从[i][j]出发的路径长度,初始化为0,在搜索[i][j]这个点时，如果f[i][j]非零，则直接返回f[i][j]的值。

class Solution {
public:
    int tx[4]={-1,1,0,0};
    int ty[4]={0,0,-1,1};
    int m;
    int n;
    int dfs(int x,int y,vector<vector<int>>& matrix,vector<vector<int>>& f)
    {
        if(f[x][y]!=0)
        {
            return f[x][y];
        }
        ++f[x][y];
        for(int i=0;i<4;i++)
        {
            int dx=x+tx[i];
            int dy=y+ty[i];
            if(dx>=0&&dx<m&&dy>=0&&dy<n&&matrix[dx][dy]>matrix[x][y])
            {
                f[x][y]=max(f[x][y],dfs(dx,dy,matrix,f)+1);
            }
        }
        return f[x][y];
    }
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m=matrix.size();
        n=matrix[0].size();
        int maxLen=0;
        vector<vector<int>> f(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                maxLen=max(maxLen,dfs(i,j,matrix,f));
            }
        }
        return maxLen;
    }
};

拓补排序

在一条上升路径中，必须先经过值小的点，才能再经过值大的点。也就是说在这个图中，值更小是值更大的先决条件，并且这个图中所有的路径是不可能构成环的。对于这种存在先决条件的无环有向图，可以用拓补排序来解决。

核心代码模式（官解）

class Solution {
public:
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    int rows, columns;

    int longestIncreasingPath(vector< vector<int> > &matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        rows = matrix.size();
        columns = matrix[0].size();
        auto outdegrees = vector< vector<int> > (rows, vector <int> (columns));
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < columns; ++j) {
                for (int k = 0; k < 4; ++k) {
                    int newRow = i + dirs[k][0], newColumn = j + dirs[k][1];
                    if (newRow >= 0 && newRow < rows && newColumn >= 0 && newColumn < columns && matrix[newRow][newColumn] > matrix[i][j]) {
                        ++outdegrees[i][j];
                    }
                }
            }
        }
        queue < pair<int, int> > q;
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < columns; ++j) {
                if (outdegrees[i][j] == 0) {
                    q.push({i, j});
                }
            }
        }
        int ans = 0;
        while (!q.empty()) {
            ++ans;
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                auto cell = q.front(); q.pop();
                int row = cell.first, column = cell.second;
                for (int k = 0; k < 4; ++k) {
                    int newRow = row + dirs[k][0], newColumn = column + dirs[k][1];
                    if (newRow >= 0 && newRow < rows && newColumn >= 0 && newColumn < columns && matrix[newRow][newColumn] < matrix[row][column]) {
                        --outdegrees[newRow][newColumn];
                        if (outdegrees[newRow][newColumn] == 0) {
                            q.push({newRow, newColumn});
                        }
                    }
                }
            }
        }
        return ans;
    }
};

自己输入数据的模式

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<utility>
using namespace std;
int n,m;
int height[105][105];
int outdegrees[105][105];
int tx[]={-1,1,0,0};
int ty[]={0,0,-1,1};
int main()
{
    cin>>n>>m;
    queue<pair<int,int>> p;
    int maxLen=0;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            cin>>height[i][j];
            outdegrees[i][j]=0;
        }
    }
    //初始化出度,出度为0的入队
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            for(int k=0;k<4;k++)
            {
                int dx=i+tx[k];
                int dy=j+ty[k];
                if(dx>=0&&dx<n&&dy>=0&&dy<m&&height[dx][dy]>height[i][j])
                    ++outdegrees[i][j];
            }
            if(outdegrees[i][j]==0)
                p.push({i,j});
        }
    }
    //开始拓补排序,类似于广度优先
    while(!p.empty())
    {
        ++maxLen;
        int size=p.size();
        for(int i=0;i<size;i++)
        {
            pair<int,int> cur=p.front();
            p.pop();
            int x=cur.first,y=cur.second;
            //更新相邻节点的出度为0的出度
            for(int k=0;k<4;k++)
            {
                int dx=x+tx[k];
                int dy=y+ty[k];
                if(dx>=0&&dx<n&&dy>=0&&dy<n&&height[dx][dy]<height[x][y])
                {
                    --outdegrees[dx][dy];
                    if(outdegrees[dx][dy]==0)
                    {
                        p.push({dx,dy});
                    }
                }
            }
        }
    }
    cout<<maxLen;
}