算法学习——LeetCode力扣补充篇6

132. 分割回文串 II

132. 分割回文串 II - 力扣（LeetCode）

描述

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是
回文串
。

返回符合要求的 最少分割次数 。

示例

示例 1：

输入：s = “aab”
输出：1
解释：只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。

示例 2：

输入：s = “a”
输出：0

示例 3：

输入：s = “ab”
输出：1

提示

1 <= s.length <= 2000
s 仅由小写英文字母组成

代码解析

动态+递归（超时）

class Solution {
public:
    int result_num = INT_MAX;
    void trak_back(vector<vector<bool>> &dp , int indnx ,int result)
    {
       
        if(indnx == dp[0].size())
        {
            if(result_num > result) result_num = result;
            return;
        }
        for(int i=0 ; i<dp[0].size() ;i++)
        {
            if(dp[indnx][i] == true )
            {
                trak_back(dp,i+1,result+1);
            }
        }
    }
    int minCut(string s) {
        int result =0;
        vector<vector<bool>> dp(s.size() , vector<bool>(s.size(),false));
        for(int i=s.size()-1 ; i>=0 ;i--)
        {
            for(int j=i ; j<s.size() ;j++)
            {
                if(s[i]==s[j] && ( j-i<=1|| dp[i+1][j-1] == true )) dp[i][j] = true;
            }
        }
       
        trak_back(dp,0,result);
        return result_num-1;
    }
};

双DP

class Solution {
public:
    int minCut(string s) {
        vector<vector<bool>> dp(s.size() , vector<bool>(s.size(),false)); //dp[i][j]为i到j内是否是回文子串
        for(int i=s.size()-1 ; i>=0 ;i--)
        {
            for(int j=i ; j<s.size() ;j++)
            {
                if(s[i]==s[j] && ( j-i<=1|| dp[i+1][j-1] == true )) dp[i][j] = true;
            }
        }
       
       vector<int> dp2(s.size() , 0); //dp2[i] 为i内最少可以分为几段

       for(int i=0 ; i<s.size() ;i++) dp2[i] = i+1;//初始化，最差的情况，一个字符一段

       for(int i=0 ; i<s.size() ;i++) 
       {
            if(dp[0][i] == true)  //如果0到i是一段，则不看0到i内部，直接dp2[i] = 1；
            {
                dp2[i] = 1;
                continue;
            }
            for(int j=0 ; j<i ;j++) //判断j+1 到 i是否是一段，如果是 在dp2[i] 和 dp[j]+1选最小
                if(dp[j+1][i] == true) dp2[i] = min(dp2[i] , dp2[j] + 1 );
            
       }
        
        return dp2[s.size()-1] - 1;
    }
};

673. 最长递增子序列的个数

673. 最长递增子序列的个数 - 力扣（LeetCode）

描述

给定一个未排序的整数数组 nums ， 返回最长递增子序列的个数 。

注意 这个数列必须是 严格 递增的。

示例

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。

提示:

1 <= nums.length <= 2000
-106 <= nums[i] <= 106

代码解析

递归（超时）

class Solution {
public:
    int result = 0;
    vector<int> path;
    int max_path = 0;
    void track_back(vector<int>& nums , int indnx)
    {
        if(path.size() > max_path)
        {
            max_path = path.size();
            result = 1;
        }else if(path.size() == max_path) result++;

        if(indnx >= nums.size() ) return;

        for(int i = indnx ;i<nums.size();i++)
        {
            if( (path.size() == 0)||(path.size() !=0 && nums[i] > path[path.size()-1]) ) 
            {
                path.push_back(nums[i]);
                track_back(nums,i+1);
                path.pop_back();
            }
        }
        return;
    }
    int findNumberOfLIS(vector<int>& nums) {
        track_back(nums,0);
        return result;
    }
};

动态规划

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size(),1);//i以内的最长子序列
        vector<int> count(nums.size(),1);//i以内最长子序列的个数
        int max_long = 1;
        for(int i=1 ; i<nums.size() ;i++)
        {
            for(int j=0 ; j<i ; j++)
            {
                if(nums[i] > nums[j] && dp[i] < dp[j] + 1) //发现更长的最长子序列
                {
                    count[i] = count[j]; 
                    dp[i] =  dp[j] + 1;
                }else if(nums[i] > nums[j] && dp[i] == dp[j] + 1) //发现和当前最长一样长的
                {
                    count[i] += count[j];
                    dp[i] = dp[i];
                }else if(nums[i] > nums[j] && dp[i] <= dp[j] + 1) //没发现最长的
                {
                    dp[i] = dp[i];
                }
                
                if(dp[i] > max_long) max_long = dp[i];
            }
        }

        int result = 0;
        for(int i=0 ; i<nums.size() ;i++)
            if(dp[i] == max_long) result += count[i];

        return result;
    }
};

841. 钥匙和房间

841. 钥匙和房间 - 力扣（LeetCode）

描述

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true，否则返回 false。

示例

示例 1：

输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2：

输入：rooms = [[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

提示

n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <= sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同

代码解析

class Solution {
public:
    
    void track_back(vector<vector<int>> &rooms ,vector<int> &keys , int indnx)
    {
        if(keys[indnx] != 0 ) return;
        
        keys[indnx]++;
       
        for(int i=0 ; i<rooms[indnx].size() ; i++)
        {
            track_back(rooms,keys,rooms[indnx][i]);
        }
        return;
    }
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        vector<int> keys(rooms.size() ,0);

        track_back(rooms,keys,0);

        for(int i=0 ; i<keys.size() ;i++) 
            if(keys[i] == 0) return false;
        
        return true;
    }
};

463. 岛屿的周长

463. 岛屿的周长 - 力扣（LeetCode）

描述

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例

示例 1：

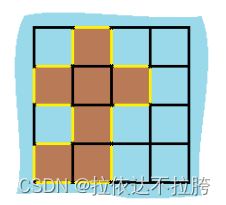
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：

输入：grid = [[1]]
输出：4

示例 3：

输入：grid = [[1,0]]
输出：4

提示

row == grid.length
col == grid[i].length
1 <= row, col <= 100
grid[i][j] 为 0 或 1

代码解析

class Solution {
public:
    int result = 0;
    int m,n;
    int dir[4][2] = {0,-1,0,1,-1,0,1,0};
    void dfs(vector<vector<int>>& grid ,int x , int y)
    {
        for(int i=0 ; i<4 ;i++)
        {
            int next_x = x + dir[i][0];
            int next_y = y + dir[i][1];
            if(next_x<0||next_x>=m||next_y<0||next_y>=n) result++;
            else if(grid[next_x][next_y] == 0) result++;
        }
        return;
    }
    int islandPerimeter(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();

        for(int i=0 ; i<m ;i++)
        {
            for(int j=0 ; j<n ;j++)
            {
                if(grid[i][j] == 1)
                    dfs(grid,i,j);
            }
        }
        return result;
    }
};