个人主页 : zxctscl
如有转载请先通知
题目
- 1. 413. 等差数列划分
- 1.1 分析
- 1.2 代码
- 2. 978. 最长湍流子数组
- 2.1 分析
- 2.2 代码
- 3. 139. 单词拆分
- 3.1 分析
- 3.2 代码
1. 413. 等差数列划分

1.1 分析
一、题目解析:
至少有三个元素才能构成等差数列,题目要求返回的是子序列等差数列的个数
二、算法原理:
-
状态表示
以i位置为结尾,找所有子数组中有多少个等差数列
dp[i]表示以i位置为结尾的所有子数组中有多少个等差数列。 -
状态转移方程
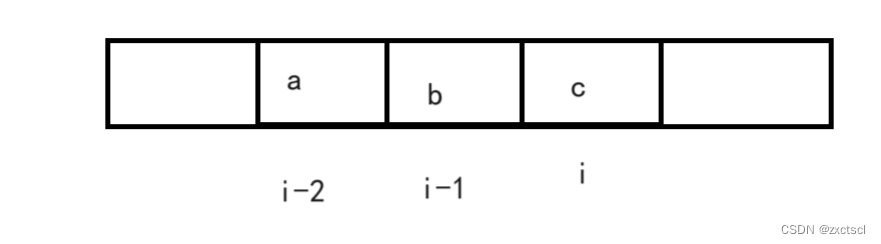
子数组是连续的,如果i位置是等差数列的子序列,那么它前面的两个至少也是构成等差数列。
第一种:考虑abc构成等差数列:c-b=b-a
如果abc能构成等差数列,那么以ab结尾的所有的等差数列再加上一个c也是等差数列。
以ab为结尾,也就是以b为结尾,那么以b结尾的所有子数组等差数列就有dp[i-1]个。但是ab就不在这个数列里面,可abc能构成等差数列,但是也多了一种,所以得多加一个1,这里的1是多加了abc这样的一种情况。
第二种:考虑abc不构成等差数列:c-b≠b-a
那么前面的数再多也不能构成等差数列,此时dp[i]=0。
状态转移方程:dp[i]=c-b==b-a?dp[i-1]+1:0
-
初始化
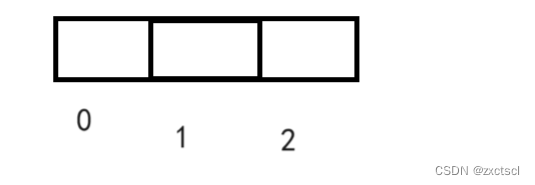
因为要三个才能构成等差数列,所以
dp[0]=0
dp[1]=0 -
填表顺序
从左往右 -
返回值
题目要求返回的不一定是最后一个位置的值,而是所有子序列等差数列的个数,所以得全部加起来。返回值就是dp表中所以元素的和。
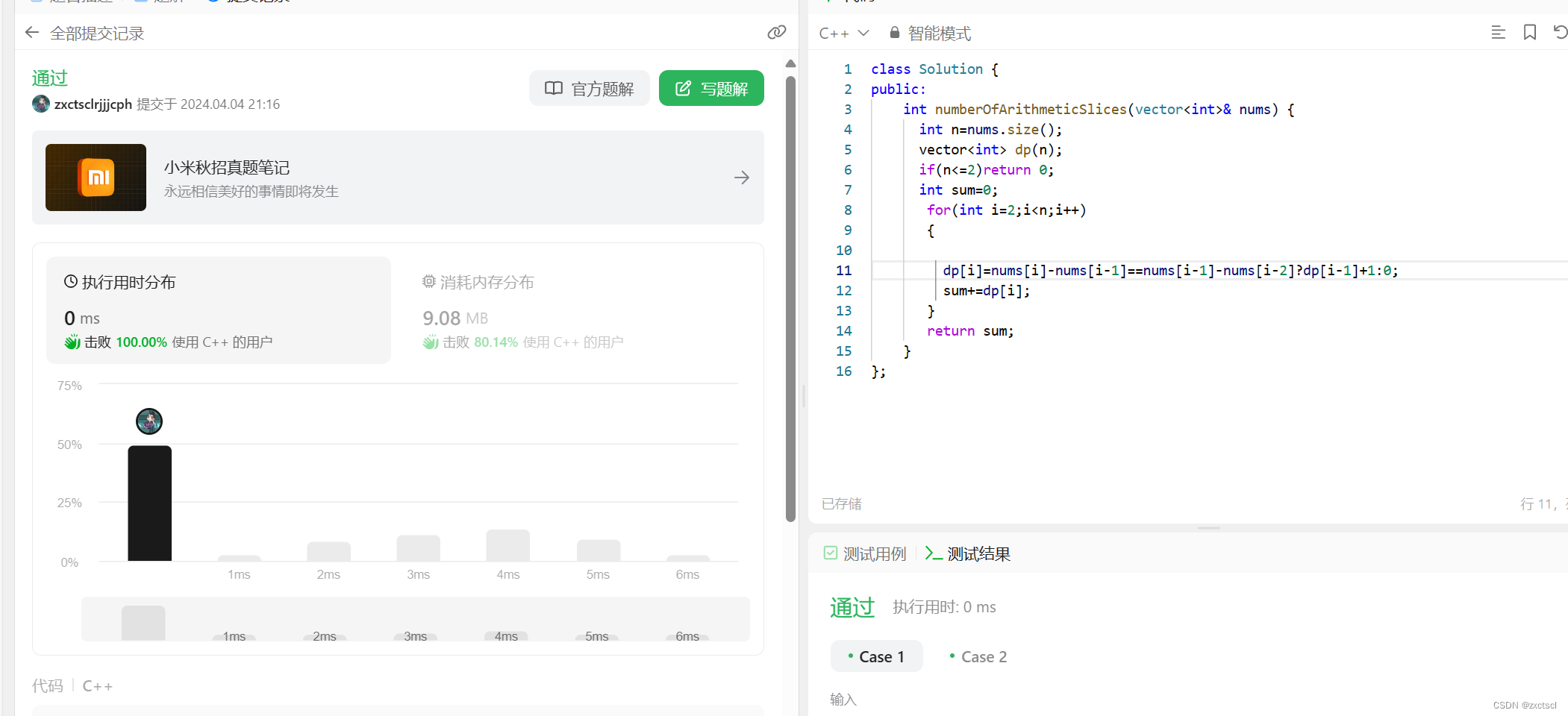
1.2 代码
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
vector<int> dp(n);
if(n<=2)return 0;
int sum=0;
for(int i=2;i<n;i++)
{
dp[i]=nums[i]-nums[i-1]==nums[i-1]-nums[i-2]?dp[i-1]+1:0;
sum+=dp[i];
}
return sum;
}
};
2. 978. 最长湍流子数组

2.1 分析
一、题目解析:
湍流数组意思是相邻两个元素大小一升一降
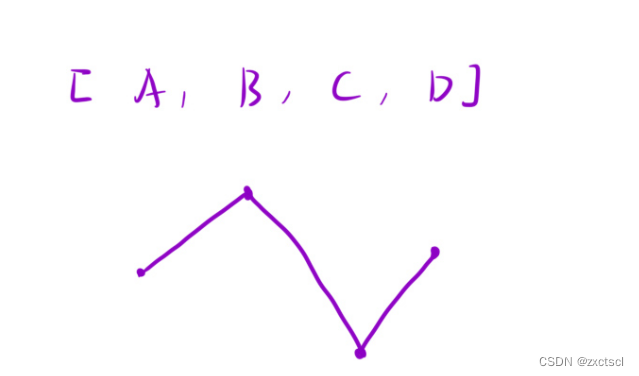
像题目给的例子1就是在第二个位置4和第三个位置都是降的就不行2。而到了第七个位置8和第六个位置8是平的没有变化,就不是湍流数组,所以例1的最大湍流数组长度就是5。

在例2中都是升的,所以最大湍流数组长度就是2。

在例1中只有一个元素,所以最大湍流数组长度就是1。

二、算法原理:
-
状态表示
以某一个位置为结尾
如果以dp[i]表示以i位置为结尾的所以子数组中,最长的湍流数组长度,那么可能会出现三种情况最后一个位置可能会出现下降趋势,也可能是上升趋势,还可以是水平的,一个状态表示不能满足情况,所以得换状态表示。
**f[i]表示i位置为结尾的所以子数组中,最后呈现“上升”**状态下,最长的湍流数组长度
**g[i]表示i位置为结尾的所以子数组中,最后呈现“下降”**状态下,最长的湍流数组长度 -
状态转移方程
在f[i]中会出现三种情况,第一种:i-1大于i,这样就不能呈现上升状态,所以i位置自己成为上升状态。第二种:i-1小于i,刚好呈现上升状态,接下来就要i-1位置为结尾成下降状态,就是g[i-1]。第三种,i位置的值和i位置相同,就得自己成为上升状态。
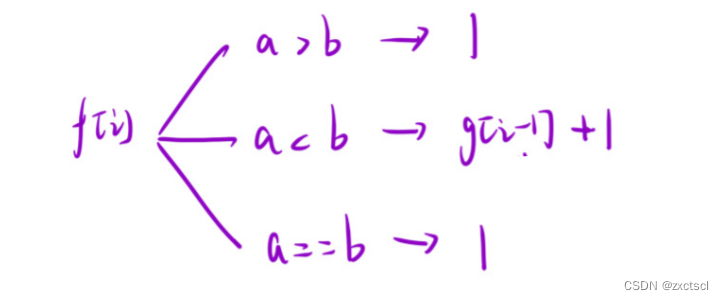
在g[i]中会出现两种情况,第一种:i-1小于i,这样就不能呈现下降状态,所以i位置自己成为下降状态。第二种:i-1打于i,刚好呈现下降状态,接下来就要i-1位置为结尾成上升状态,就是f[i-1]。第三种,i位置的值和i位置相同,就得自己成为下降状态。
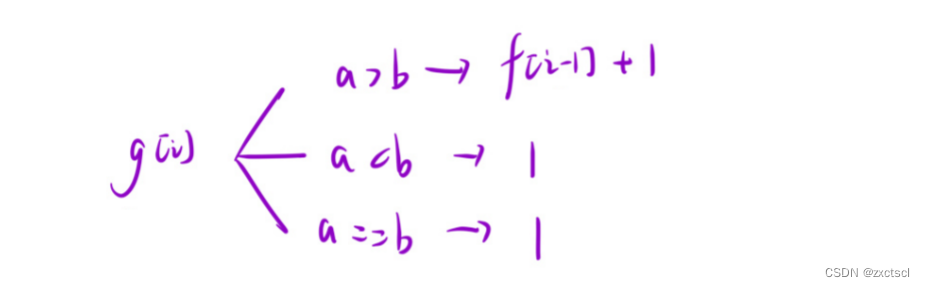
- 初始化
在f表和g表中最差的情况就是1,所以把表中元素全部初始化为1。这样就减少了很多判断情况。
-
填表顺序
从左往右
两个表一起填 -
返回值
返回f表和g表中最大的那个
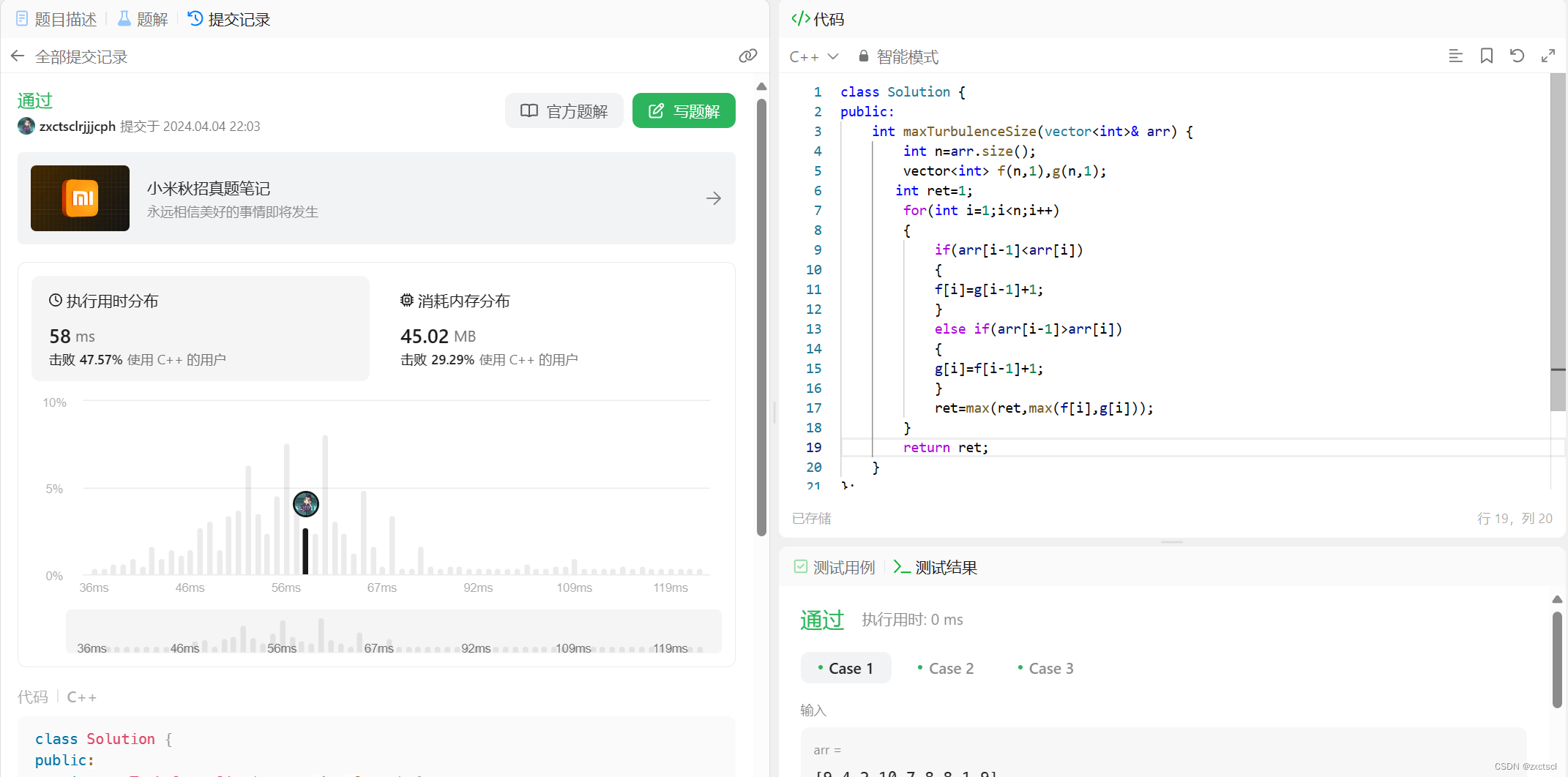
2.2 代码
class Solution {
public:
int maxTurbulenceSize(vector<int>& arr) {
int n=arr.size();
vector<int> f(n,1),g(n,1);
int ret=1;
for(int i=1;i<n;i++)
{
if(arr[i-1]<arr[i])
{
f[i]=g[i-1]+1;
}
else if(arr[i-1]>arr[i])
{
g[i]=f[i-1]+1;
}
ret=max(ret,max(f[i],g[i]));
}
return ret;
}
};
3. 139. 单词拆分

3.1 分析
一、题目解析:
在给的 wordDict 字典里面可以重复使用某一个单词,还没有要求全部使用。
看一下给的例2:s里面给的字符串就可以在wordDict 字典里面找到就返回true。

例3:第一单词不管是选择cat还是cats最后剩下的og在wordDict 字典里面都没有找到,就返回false。

二、算法原理:
-
状态表示
以某一个位置为结尾
dp[i]表示以i位置为结尾的[0,i]区间内的字符串,能否被字典中的单词拼接而成。能被拼接而成就是true,不能就是false。 -
状态转移方程
根据最后一个位置的情况来划分问题:前面那一部分单词,加上最后一个单词,而最后一个单词中的i,只要能确定前面部分能拼接而成,并且最后一个单词在wordDict 字典里面能找到,那么这个字符串就能拼接而成。
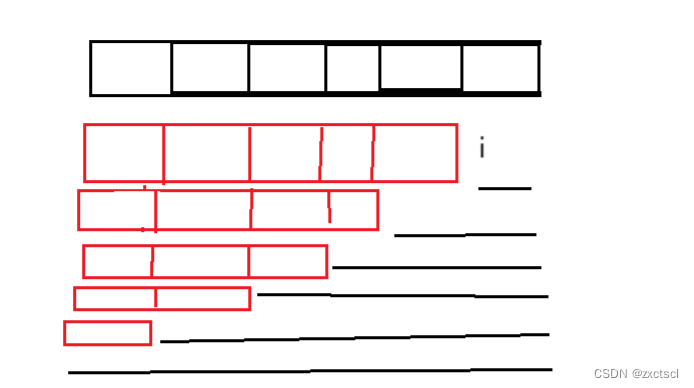
那么在设一个变量j来作为左边部分的最后一个下标,左边这个字符串的开始在0,结尾在j-1,这个区间能否作为字典中的单词拼接而成就是dp[j-1],右边这个位置就[j,i]组成的单词是否在字典中就行。左右两种情况都为true的时候就能拼接。
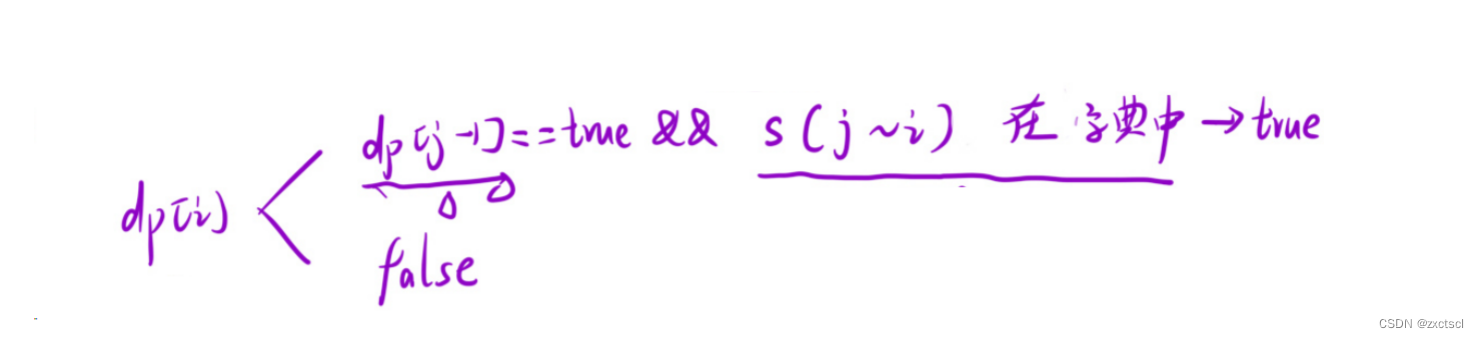
-
初始化
为了dp[j-1]不越界,就加一个虚拟节点。为了保证后面的填表顺序是正确,那么dp[0]=true。
还得注意下标的映射关系,这里加了一个新节点,那么s表就得加一个辅助字符。
-
填表顺序
从左往右 -
返回值
题目要求返回是s字符串能否被拼接,就是dp[n]。
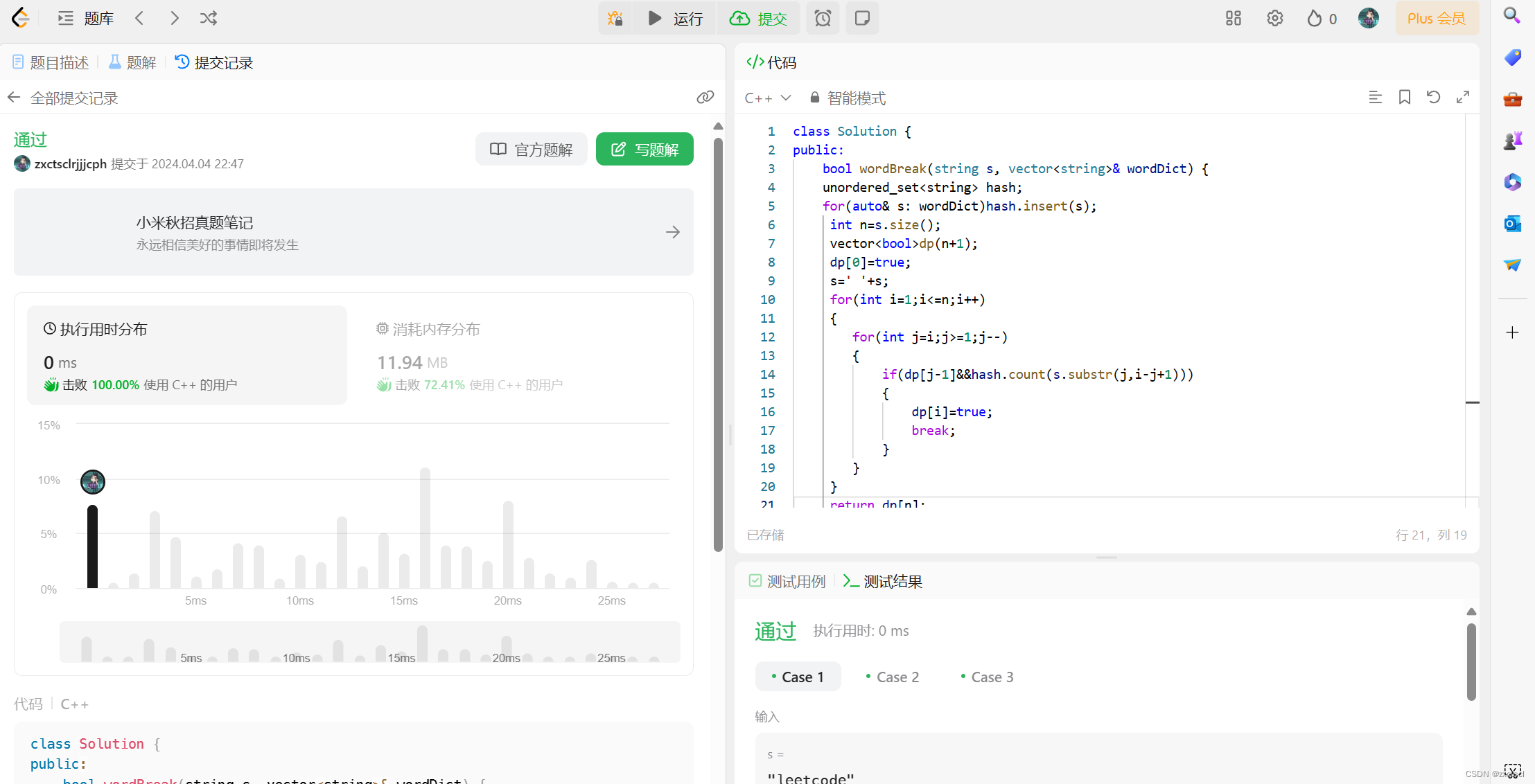
3.2 代码
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> hash;
for(auto& s: wordDict)hash.insert(s);
int n=s.size();
vector<bool>dp(n+1);
dp[0]=true;
s=' '+s;
for(int i=1;i<=n;i++)
{
for(int j=i;j>=1;j--)
{
if(dp[j-1]&&hash.count(s.substr(j,i-j+1)))
{
dp[i]=true;
break;
}
}
}
return dp[n];
}
};/* */
有问题请指出,大家一起进步!!!









![[AutoSar]BSW_Memory_Stack_004 创建一个简单NV block并调试](https://img-blog.csdnimg.cn/direct/cf7515a471fb4dabb035da6bb88e0278.png)