Facing Changes: Continual Entity Alignment for Growing Knowledge Graphs

面对变化：不断增长的知识图谱的持续实体对齐

Abstract

实体对齐是知识图谱(KG)集成中一项基本且重要的技术。多年来，实体对齐的研究一直基于知识图谱是静态的假设，忽略了现实世界知识图谱增长的本质。随着知识图谱的增长，之前的对齐结果需要重新审视，同时新的实体对齐等待被发现。在本文中，我们提出并深入研究了一个现实但尚未探索的环境，称为持续实体对齐。为了避免每当新实体和三元组出现时在整个 KG 上重新训练整个模型，我们为此任务提出了一种持续对齐方法。它根据实体邻接关系重建实体的表示，使其能够使用现有邻居快速、归纳地生成新实体的嵌入。它选择并重放部分预对齐的实体对，以仅训练部分知识图谱，同时提取值得信赖的对齐以增强知识。由于不断增长的知识图谱不可避免地包含不可匹配的实体，与以前的工作不同，该方法采用双向最近邻匹配来找到新的实体对齐并更新旧的对齐。此外，我们还通过模拟多语言 DBpedia 的增长来构建新的数据集。大量的实验表明，我们的持续对齐方法比基于再训练或归纳学习的基线更有效。

1 Introduction

实体对齐，也称为实体匹配或实体解析，一直是语义网和数据库社区中的一个长期研究主题。该任务的目的是在不同的知识图(KG)中匹配具有不同URI的相同实体。例如，来自DBpedia的两个实体http://dbpedia.org/RESOURCE//Hangzhou 和 http://zh.dbpedia.org/resource/杭州 以不同的语言引用了同一个中国城市，杭州是ISWC2022会议的举办地。早期研究主要探索字面相似性与概率或语义推理来匹配实体。然而，这些方法受到不同知识图谱的符号异质性的阻碍，特别是跨语言知识图谱。为了解决这个问题，最近基于嵌入的方法努力构建一个统一的向量空间来表示不同的知识图谱，并使用实体嵌入来推断实体相似性。此外，通过对齐各种知识图谱构建的统一空间的嵌入被证明对于下游任务非常有用，例如跨语言知识转移和多语言知识图谱补全。因此，作为知识融合和迁移的支柱，基于嵌入的实体对齐受到越来越多的关注。

然而，现有的基于嵌入的实体对齐方法假设了静态知识图谱的理想化场景，忽略了许多现实世界的困难，例如对齐不完整、知识图谱增长和对齐增长。在本文中，我们认为实体对齐不是一次性任务。我们提出并研究了一种新的设置，即不断增长的知识图谱和不完整的知识图谱之间的持续实体对齐。我们的动机来自现实世界 KG 的增长和不完整性。例如，DBpedia 的发布机器人每月提取约 210 亿个新三元组，Wikidata以每周为周期发布数据转储。新的实体和三元组带来了新的对齐方式被发现和使用。为修正之前的对齐提供新的线索。图 1 给出了一个示例。

这种真实场景对基于嵌入的实体对齐提出了新的挑战。第一个挑战是如何以有效且高效的方式学习新实体的嵌入。当知识图谱增长时，预训练的实体对齐模型第一次看到新的实体，因为新的三元组给知识图谱带来了结构变化。

为了处理新实体，从头开始重新训练模型的成本很高。此外，归纳实体嵌入对结构变化的适应性较差。因此，需要对预训练模型进行重要更新以合并新实体和新三元组。第二个挑战是如何捕捉新旧实体的潜在一致性。在实际情况中，知识图谱总是包含未知的不可匹配实体，这需要更可靠的对齐检索策略，而不是简单地对测试集中的候选者进行排名。此外，由于新实体通常链接很少，捕获新实体的潜在对齐变得更加困难。第三个挑战是如何将旧的预测对齐与新的预测相结合。在我们的设置中，每次 KG 增长时我们都会输出对齐结果。新旧结盟不可避免地会发生冲突。我们需要一个有效的整合策略来组合它们并更新最终的对齐方式。

作为解决这些挑战的首次尝试，我们提出了一种持续实体对齐方法 $ContEA$。我们的关键想法是微调预训练模型以合并新实体和三元组，同时捕获潜在的实体对齐。具体来说，我们使用 $Dual-AMN$ (一种著名的对齐模型)作为我们的基础编码器。为了使其能够有效地处理新实体，我们设计了一个实体重建目标，它允许编码器仅使用相邻子图来生成实体嵌入。为了从嵌入空间检索对齐，我们提出了一种双向最近邻搜索策略。当且仅当两个实体是彼此最近的邻居时，才预测它们是对齐的。当新的实体和三元组出现时，$ContEA$ 根据变化的结构对预训练模型进行微调。为了捕获潜在的实体对齐，我们重放部分已知的对齐以避免知识遗忘并选择高置信度预测来增强知识。

为了支持这项新的实用任务的研究，我们基于广泛使用的基准 $DBP15K$ 构建了三个新数据集，其中包含三个跨语言数据集，即$ZH-EN$、$JA-EN$ 和 $FR-EN$。对于每个数据集，我们通过将新实体和新三元组添加到前面的快照中来构建六个快照（即 $t=0,1,2,3,4,5$），以模拟 KG 的增长。我们对数据集进行了广泛的实验。我们的方法优于使用再训练或归纳嵌入技术的强大基线，同时时间成本较低。我们的数据集和源代码是公开的，以促进未来的研究。

2 Problem Statement

我们将 KG 定义为三元组 G = { E , R , T } \mathcal{G}=\{\mathcal{E},\mathcal{R},\mathcal{T}\} G={E,R,T}，其中 $\mathcal{E}$ 和 $\mathcal{R}$ 分别表示实体和关系的集合。 $\mathcal{T}\subseteq \mathcal{E}\times \mathcal{R}\times \mathcal{E}$ 是关系三元组的集合。给定两个 KG G 1 = { E 1 , R 1 , T 1 } \mathcal{G_1}=\{\mathcal{E_1},\mathcal{R_1},\mathcal{T_1}\} G1​={E1​,R1​,T1​} 和 G 2 = { E 2 , R 2 , T 2 } \mathcal{G_2}=\{\mathcal{E_2},\mathcal{R_2},\mathcal{T_2}\} G2​={E2​,R2​,T2​}，实体对齐的目的是识别 ${\mathcal{G}}_1$ 和 ${\mathcal{G}}_2$ 中引用同一现实世界对象的实体，即寻求一组对齐$\mathcal{A}=\{(e_1,e_2)\in {\mathcal{E}}_s\times {\mathcal{E}}_t|e_1\equiv e_2\}$，其中$“\equiv ”$表示等价。通常预先提供一小组种子实体对齐 ${\mathcal{A}}_{\mathrm{s}}\subset \mathcal{A}$ 作为锚点（即训练数据），以帮助对齐其余实体。

不时会有新的三元组出现并添加到KG中，这带来了KG的规模增长。我们提出生长KG的定义如下：

定义1（不断增长的知识图((Growing knowledge graphs)）。增长的KG $\mathcal{G}$ 是一系列快照 $\mathcal{G}=({\mathcal{G}}^0,{\mathcal{G}}^1,\dots ,{\mathcal{G}}^T)$，其中上标数字表示不同的时间戳。对于任意两个连续的时间戳 G t = { E t , R t , T t } \mathcal{G}^{t}=\{\mathcal{E}^{t},\mathcal{R}^{t},\mathcal{T}^{t}\} Gt={Et,Rt,Tt}和 G t + 1 = { E t + 1 , R t + 1 , T t + 1 } \mathcal G^{t+1} = \{\mathcal{E}^{t+1},\mathcal{R}^{t+1},\mathcal{T}^{t+1}\} Gt+1={Et+1,Rt+1,Tt+1}，存在 ${\mathcal{E}}^t\subseteq {\mathcal{E}}^{t+1}$, ${\mathcal{R}}^t\subseteq {\mathcal{R}}^{t+1}$ 和 ${\mathcal{T}}^t\subseteq {\mathcal{T}}^{t+1}$。

在此定义中，在 $t$ 和 $t+1$ 之间的 $\Delta {\mathcal{T}}^{\mathrm{t}+1}$中每个新添加的三元组包含零个、一个或两个新实体。考虑到知识图谱中的关系集远不如实体的多样化，我们在本文中忽略了新关系的出现，并假设知识图谱中的关系是预先定义的。

在不断增长的知识图谱上实践实体对齐。我们提出持续实体对齐的任务并给出其定义如下：

定义 2（持续实体对齐(Continual entity alignment)）。给定两个不断增长的 KG ${\mathcal{G}}_1$ 和 ${\mathcal{G}}_2$，以及种子实体对齐 ${\mathcal{A}}_s$ 在时间 $t=0$ 时，在时间 $t$ 的连续实体对齐旨在基于当前学习的 KG 嵌入和对齐模型在 ${\mathcal{G}}_1^t$ 和 ${\mathcal{G}}_2^t$ 之间找到潜在的实体对齐 ${\mathcal{A}}_p^t$。

在此定义中，${\mathcal{A}}_s$的大小是恒定的，而 ${\mathcal{A}}_p^t$随着时间的推移而增长，因为新实体可能会发现新的实体对齐。考虑到种子实体对齐通常是有缺陷且难以获得的，我们不假设新快照带来新的种子对齐来增强训练数据。也就是说 $t>0$ 时刻的快照 ${\mathcal{A}}_s$ 与 $t=0$ 时刻的快照 ${\mathcal{A}}_s$ 相同。

3 Methodology

在本节中，我们介绍所提出的连续实体对齐方法$ContEA$。图2描述了它的框架。它由两个模块组成：基于子图的实体对齐模块以及嵌入和对齐更新模块。以下是它们的简要概述：

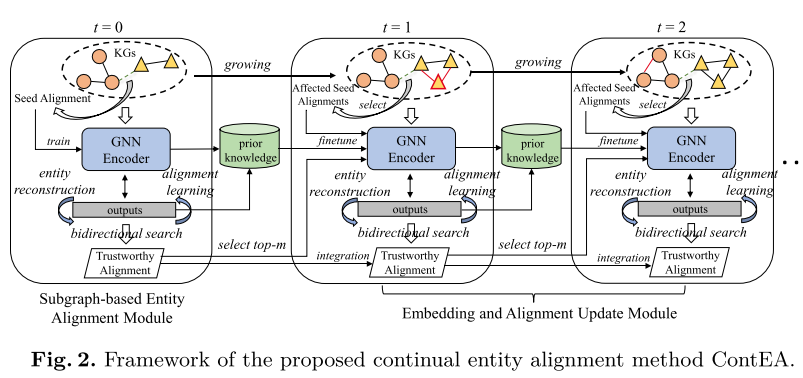
3.1 Subgraph-based Entity Alignment 基于子图的实体对齐

该模块基于 GNN构建，GNN通过聚合其邻域子图来表示实体。GNN背后的关键假设是具有相似邻域的实体看起来很接近，这使得 GNN 可扩展以表示新实体。请注意，我们并不关注如何开发强大的 GNN 来进行实体对齐，而是关注如何以有效且高效的方式合并新实体和三元组以实现持续的实体对齐。

子图编码器。 我们采用基于 GNN 的 Dual-AMN编码器作为我们的子图编码器，因为它的有效性和简单性。 Dual-AMN的编码器由捕获单个KG内的结构信息的内图层（即$Aggregato{r}_1$）和基于$Aggregato{r}_1$的输出捕获跨图匹配信息的跨图层（$Aggregato{r}_2$）组成。从技术上讲，$Aggregato{r}_1$是一个 2 层关系感知 GNN，$Aggregato{r}_2$是一个代理注意力网络，将实体与代理节点列表连接起来。总体而言，给定一个实体 $e$，其经过 Dual-AMN 编码后的表示为

$$\text{Encoder}(e)={\text{Aggregator}}_2({\text{Aggregator}}_1(e,{\mathcal{N}}_e),{\mathcal{E}}_{\text{proxy}}),(1)$$

其中 $Aggregato{r}_1()$ 聚合实体本身及其关系邻居 ${\mathcal{N}}_e$ 以生成其嵌入，$Aggregato{r}_2()$将输出嵌入与代理节点 ${\mathcal{E}}_{proxy}$ 组合以生成实体的最终表示。为了节省篇幅，我们在这里不介绍 Dual-AMN 的详细技术。有兴趣的读者可以参考其原始论文https://arxiv.org/pdf/2103.15452.pdf了解更多详细信息。

实体重建。 随着 KG 的增长，预训练的 GNN 编码器会遇到新的实体和三元组。关键的挑战是如何将看不见的实体合并到编码器中。随机初始化新实体的嵌入可能不利于之前优化的嵌入空间并导致表示不一致。基于嵌入的实体对齐的典型假设是，如果两个实体的邻域子图相似（即两个子图具有相似或预先对齐的实体），则两个实体相似。受此启发，我们提出了一个自监督学习目标，使编码器能够使用其邻域子图重建实体：

$${\mathcal{L}}_{\text{reconstruct}}=\sum _{e\in \mathcal{E}}{\Vert \mathbf{e}-\frac{1}{|{\mathcal{N}}_e|}\sum _{e^{\prime }\in {\mathcal{N}}_e}{\mathbf{e}}^{\prime }\Vert }_2^2.(2)$$

这里，${\mathcal{N}}_e$表示 $e$的一跳邻居集合。该目标最小化实体与其相邻子图嵌入（所有相邻嵌入的平均向量）之间的距离。

对齐学习。 给定编码器的输出，对齐学习的目的是收集相似的实体对并距离不相似的实体对。通过负采样对不同的实体对进行建模。继 Dual-AMN 之后，我们还采用 LogSumExp 函数来计算损失：

$${\mathcal{L}}_{\mathrm{align}}=\log [1+\sum _{(e_1,e_2)\in {\mathcal{A}}_s}\sum _{(e_1,e_2^{\prime })\in {\mathcal{A}}_{e_1}^{\mathrm{neg}}}\exp (\gamma (\lambda +\mathtt{s}\mathtt{in}(e_1,e_2)-\mathtt{s}\mathtt{im}(e_1,e_2^{\prime }))\left)\right],(3)$$

其中 ${\mathcal{A}}_{e_1}^{\mathrm{neg}}$ 表示为实体 $e_1$生成的负对齐。 $\gamma$是比例因子，$\lambda$是用于分离种子对齐对和负对的相似性的余量。余弦用于计算嵌入相似度，即 $\text{sim}(e_1,e_2)=\cos (\text{Encoder}(e_1),\text{Encoder}(e_2)$。我们采用批量负生成方法。具体来说，对于实体 $e_1$，训练批次中的其他实体（例如 $e_2^{\prime }$）充当其负对应物以生成负对 ${\mathcal{A}}_{e_1}^{\mathrm{neg}}$ 。基于子图的实体对齐模块 ${\mathcal{L}}_1$ 的最终学习目标是 ${\mathcal{L}}_{align}$ 和 ${\mathcal{L}}_{reconstruct}$的组合，${\mathcal{L}}_{reconstruct}$上的权重为 $\alpha$：

$${\mathcal{L}}_1={\mathcal{L}}_{\text{align}}+\alpha \cdot {\mathcal{L}}_{\text{reconstruct}}.(4)$$

值得信赖的对齐搜索。 对齐学习完成后，我们根据优化的嵌入空间检索可信的实体对齐作为预测。之前基于嵌入的实体对齐方法假设一个 KG 中的每个实体必须在另一个 KG 中具有对应项。典型的推理过程是最近邻搜索，即它寻求

$${\hat{e}}_2=\arg \underset{e_2\in {\mathcal{E}}_2}{\min }\pi (\text{Encoder}(e_1),\text{Encoder}(e_2)),(5)$$

其中 $\pi ()$ 是对齐搜索的度量，${\hat{e}}_2$ 是 $e_1$ 的预测对应项。然而，这种“理想化”的假设在现实环境中可能并不成立，因为两个知识图谱中有许多不匹配的实体。为了解决这个问题并改进对齐搜索，我们提出了一种称为双向最近对齐搜索的无参数策略。它在一个 KG 中搜索另一个 KG 中实体的最近邻居。当且仅当 $e_2={\hat{e}}_2$ 且 $e_1={\hat{e}}_1$ 时，对齐对 $(e_1,e_2)$ 才是值得信赖的对齐。其他对齐对被丢弃。

3.2 Embedding and Alignment Update 嵌入和对齐更新

在时间 $t>0$ 时，KG 的关系结构随着新三元组的出现而发生变化。它需要在捕获结构变化的同时为新实体生成嵌入。为了解决这一挑战，我们建议通过部分种子对齐和选定的可信对齐来微调 GNN 编码器和新实体嵌入。微调后，根据更新的模型和嵌入检索新的可信实体对齐。新的预测对齐用于使用启发式策略来完成和更新在时间 $t-1$ 发现的旧对齐。

编码器微调。 我们使用前一个模块/时间中学到的参数来初始化编码器。由于我们的实体重建目标，编码器能够初始化新实体 $e$ 的嵌入，如下所示：

$$\text{Encoder}(e)={\text{Aggregator}}_2({\text{Aggregator}}_1(\text{MP}({\mathcal{N}}_e^{\prime })),{\mathcal{E}}_{\text{proxy}}),(6)$$

其中 ${\mathcal{N}}_e^{\prime }$ 表示新实体 $e$ 的可见邻居。$MP()$ 是使用 ${\mathcal{N}}_e^{\prime }$生成 $e$ 嵌入的均值池化过程。

基于新实体和现有实体的输出嵌入，我们对 GNN 编码器进行微调。具体来说，我们冻结内图层 $Aggregato{r}_1$，同时使跨图 $Aggregato{r}_2$可学习。对于单个 KG，新数据的到来不会改变邻居聚合模式，因为 KG 的模式保持一致（没有新的关系或实体域）。但在所提出的场景中，两个 KG 独立且不对称地增长。需要对匹配网络进行微调，做出调整和新的发现。

对于训练数据，考虑到潜在的实体对齐更有可能发生在锚点附近，我们仅重播包含新三元组中涉及的锚点的受影响的种子实体对齐。这有助于新实体的协调，而这原本由于其程度低而很困难。此外，为了帮助对齐来自更广泛和更动态区域的实体，我们选择具有最高相似性分数的 $top-m$ 预测可信对齐，并将它们视为“新锚点”。

我们对获得的受影响种子对齐（简称 ASA）和 $m$ 个选定的可信对齐（简称 TA）上的 GNN 编码器和新实体嵌入进行微调。我们对 $m$ 个值得信赖的对齐的学习损失使用权重 $\beta$ 来平衡其重要性。最终finetuning的损失函数${\mathcal{L}}_2$为

$${\mathcal{L}}_2={\mathcal{L}}_{\text{align}}(ASA)+\alpha \cdot {\mathcal{L}}_{\text{reconstruct}}+\beta \cdot {\mathcal{L}}_{\text{align}}(TA).(7)$$

值得信赖的对齐更新。 微调后，可以使用更新的实体嵌入和模型检索一组新的可信对齐。有必要将其与先前发现的值得信赖的对齐方式结合起来，因为它们是从不同的快照中收集的，并且可以相互补充以产生更好的结果。在这里，我们采用启发式策略来整合它们。我们在两个新实体之间保持新的值得信赖的联盟。但对于导致对齐冲突与之前值得信赖的对齐（即一个实体与不同实体对齐）的新对齐，我们决定保留具有更高相似性分数的对齐。随着知识图谱的增长，可信实体联盟的规模不断累积。

3.3 Put It All Together

算法 1 描述了 $ContEA$ 用于持续实体对齐的训练和微调细节。第 1-3 行描述了时间 $t=0$ 时基于子图的实体对齐模块的过程。第 4-8 行描述了时间 $t>0$ 时嵌入和对齐更新模块的过程。

4 Experiments

4.1 New Datasets for Continual Entity Alignment

由于缺乏建议设置的现成基准，我们基于 $DBP15K$ 构建新的数据集。对于每个 $DBP15K$ 的跨语言实体对齐数据集，我们使用其两个 KG 作为第一个快照（即 t = 0）。$DBP15K$ 仅考虑三元组的头实体之间的实体对齐，而忽略其他实体对齐对。因此，我们首先使用DBpedia中的语言间链接完成参考实体对齐，从而在第一个快照中产生超过15K的参考对齐对。然后，将参考实体对齐分为训练集、验证集和测试集（即 ${\mathcal{A}}_s$、${\mathcal{A}}_v$ 和 ${\mathcal{A}}_p^0$），比例为 2:1:7。我们进一步构建五个快照来模拟 KG 的增长：

• 在时间 $t>0$ 时，我们首先从 DBpedia 收集包含 ${\mathcal{G}}_1^{t-1}$ 和 ${\mathcal{G}}_2^{t-1}$中实体的关系三元组。然后，在这些三元组中，我们删除在时间 $t-1$ 时看到的三元组，并从剩余的三元组中采样新的三元组，其大小为先前快照中三元组的 20%。将新的三元组添加到 ${\mathcal{G}}_1^{t-1}$和 ${\mathcal{G}}_2^{t-1}$ 中，我们创建快照 ${\mathcal{G}}_1^t$ 和 ${\mathcal{G}}_2^t$。
• 然后，我们通过添加来自 DBpedia 的附加关系三元组来完成 ${\mathcal{G}}_1^t$ 和 ${\mathcal{G}}_2^t$，其中头实体和尾实体都在快照中，导致三元组大小增长超过 20%。
• 最后，我们检索新添加的实体带来的新实体对齐对，并将它们添加到快照 $t$ 的测试集 ${\mathcal{A}}_p^t$ 中。,训练集 ${\mathcal{A}}_s$ 或验证集 ${\mathcal{A}}_v$ 仍然遵循时间 $t=0$ 时第一个快照中的情况。我们不假设新快照引入新的训练数据，因为获得新兴实体的种子对齐通常比为旧实体找到种子对齐更困难,现实世界中的实体。

我们数据集的详细统计数据如表 1 所示。

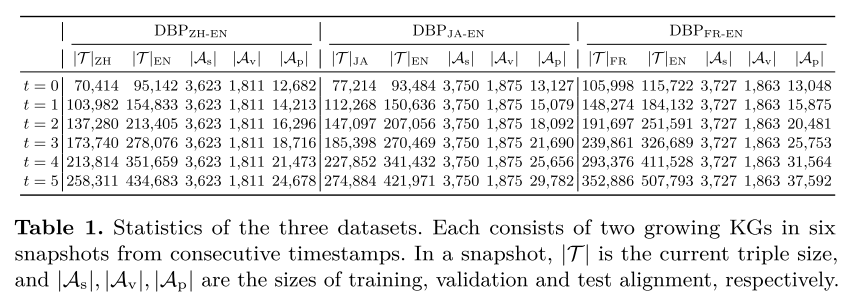
4.2 Baselines

我们将 ContEA 与两组实体对齐方法进行比较。

• 再训练基线(Retraining baselines)。由于大多数现有的基于嵌入的 EA 方法都是为静态 KG 设计的，因此每次新的三元组出现时都需要重新训练。在这里，我们选择代表性的基于翻译的方法 MTransE，以及几种最先进的基于 GNN 的方法，包括 GCN-Align、AlignE、AliNet、KEGCN 和 Dual-AMN 作为我们的基线。
• 归纳基线(Inductive baselines)。唯一关注 KG 增长的实体对齐方法是 DINGAL。我们选择建议的变体之一 DINGAL-O 作为基线，它可以处理我们的场景。此外，由于有一些归纳知识图谱嵌入（KGE）方法可以为新实体生成嵌入，因此我们探索它们与静态方法的组合来解决我们的任务。在这里，我们选择两种代表性的归纳式 KGE 方法 MEAN 和 LAN 作为实体表示层，并将它们与 Dual-AMN 结合起来。我们用 $MEA{N}^{+}$ 和 $LA{N}^{+}$ 表示两个基线。

4.3 Experiment Settings

评估指标。 在每个时间 $t$，使用双向最近邻搜索和对齐集成来获得最终的可信对齐。详细内容在第 3.1和3.2节中有描述。然后，我们将最终的可信对齐与黄金测试对 At p 进行比较。我们报告准确率、召回率和 F1 分数作为评估指标。

执行。 我们使用 PyTorch 实现 ContEA、Dual-AMN、$MEA{N}^{+}$ 和 $LA{N}^{+}$。对于其他再训练基线，我们使用开源库中的实现。我们将嵌入维度设置为 100。嵌入相似度度量为 CSLS。我们对超参数使用网格搜索并提前停止以找到最佳性能。特别是对于 ContEA，我们设置 $\alpha =0.1$、$\beta =0.1$ 和 $m=500$。更详细的超参数设置可以在我们的 GitHub 存储库中找到。为了公平比较，所有基线仅依赖 KG 的结构信息，不使用预训练模型进行初始化。

4.4 Results

一般结果。 我们对构建的数据集进行了实验，结果如表 2、表 3 和表 4 所示。与基线相比，ContEA 在发现潜在实体对齐方面达到了最佳性能。在 $DB{P}_{ZH-EN}$、$DB{P}_{JA-EN}$ 和 $DB{P}_{FR-EN}$ 的 6 个快照上，其 F1 分数平均比最佳基线 Dual-AMN 分别高出 27.1%、19.4% 和 15.2%。 ContEA 优于再训练方法的性能是因为 ContEA 可以迭代地利用过去快照中的先验知识（例如，先前预测的对齐和模型参数）。此外，ContEA 通过整合新旧可信对齐来共同获得预测的实体对齐，而不是在再训练中完全忽略旧的预测。对于归纳基线，$MEA{N}^{+}$和$LA{N}^{+}$的性能比ContEA和Dual-AMN差，这表明在不调整对齐网络的情况下直接添加归纳KGE层并不能给出令人满意的性能。 DINGALO 也显示出不令人满意的结果，因为它是纯归纳式的并且不更新对齐网络。此外，我们可以注意到所有方法的性能都会随着时间的推移而下降。这是由于对齐候选的搜索空间扩大，以及种子对齐与待对齐对齐的比率下降所致。这两者都会增加实体不匹配的可能性。

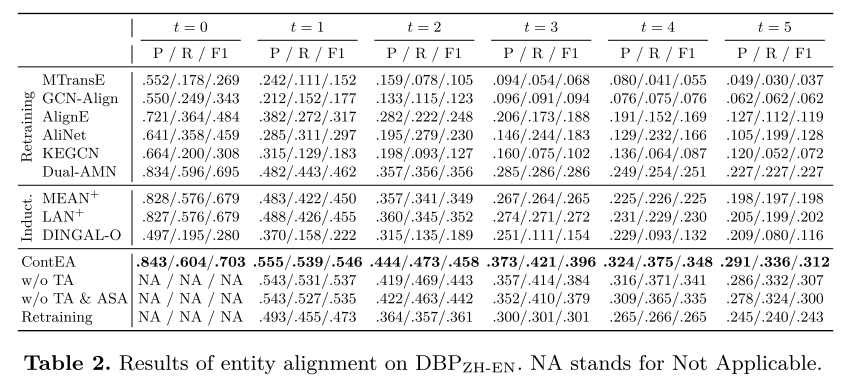
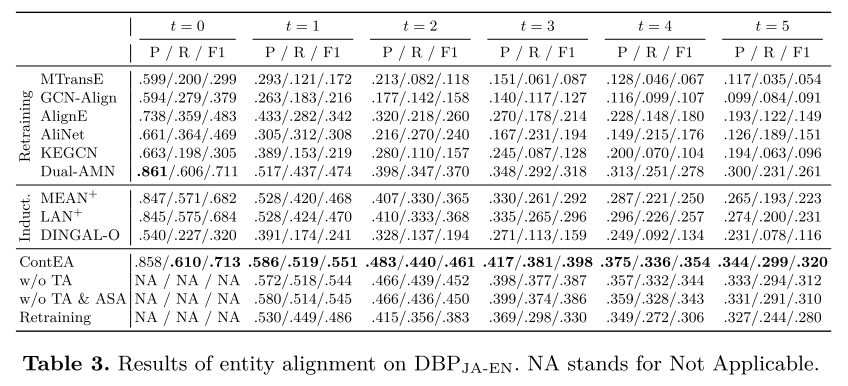
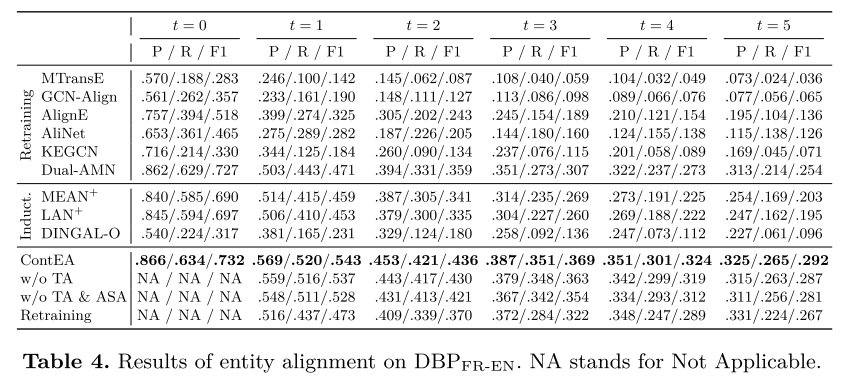
消融研究。 为了研究 ContEA 每种设计的影响，也为了在 ContEA 和基线之间进行更公平的比较，我们放弃了 ContEA 的某些部分，并提出了三种变体，如下所示：

• ContEA 不带 TA。在微调过程中，我们丢弃选定的可信实体对齐，仅对受影响的种子对齐进行训练。
• ContEA 不含 TA 和 ASA。我们丢弃选定的可信对齐和受影响的种子对齐。因此，我们的方法不需要微调并简化为归纳方法。实体重建方法使用其邻居为新实体生成嵌入。
• ContEA 再培训。与再训练基线相同，ContEA 将每个快照视为 $t=0$。旧预测的实体对齐完全被新预测的实体对齐取代，而不是集成。

我们在表 2、表 3 和表 4 中显示了三个变体的结果。这些变体在 $t=0$ 时继承了经过训练的 ContEA，并在之后分别执行。当丢弃选定的可信对齐时，我们可以注意到性能下降。如果进一步降低受影响的种子排列，则会出现更大的下降。这证明了所选择的可信对齐和受影响的种子对齐重放的有效性。对于ContEA再训练，虽然它的表现比ContEA差很多，但它仍然优于所有再训练基线，包括Dual-AMN，这表明了实体重建的有效性。

发现新的对齐方式。 接下来，我们展示 ContEA 在发现新实体对齐方面的性能。在时间 t = { 1 , 2 , 3 , 4 , 5 } t = \{1, 2, 3, 4, 5\} t={1,2,3,4,5} 时，我们收集涉及新实体的最终预测对齐，并通过将其与包含新实体的黄金测试对齐进行比较来计算召回值。我们在表 5 中显示了 $DB{P}_{ZH-EN}$ 上的结果。ContEA 相对于所有基线达到了最高的召回率，这表明我们的方法在发现新实体的对齐方面的优势。我们还可以注意到，新实体的黄金对齐召回率明显低于所有黄金对齐召回率。这是因为新实体往往是稀疏链接的，这阻碍了对齐模型正确匹配它们。此外，图 3 说明了 ContEA 的总正确预测比对的增长。在时间 $t$，正确预测的总对齐大小计算为 $|{\mathcal{A}}_{\mathrm{p}}^t|\times \mathrm{Recall}$（表 2 中的 R）。结果表明，随着 KG 的增长，ContEA 可以找到越来越大的正确实体对齐，这满足了持续实体对齐的建议。

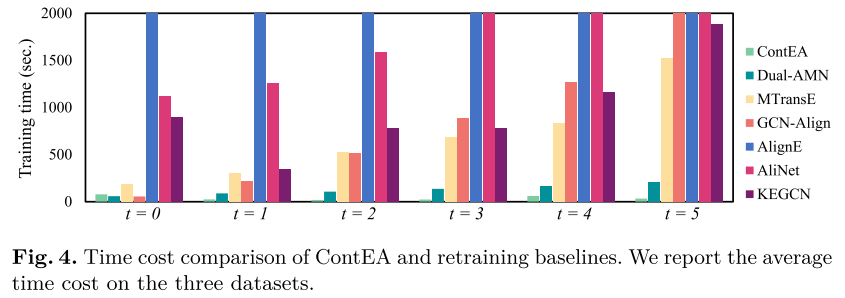
效率。 我们将 ContEA 的训练效率与再训练基线进行比较。请注意，由于归纳基线在新三元组出现时没有训练过程，因此我们不将它们包含在此处。我们在配备 512GB 内存、两个 Xeon Gold 6326 CPU 和四个 RTX A6000 GPU 的服务器上运行所有实验。图 4 描述了不同快照下三个数据集的平均时间成本。为了更好的呈现，我们将垂直轴的上限设置为2000秒。我们可以看到 ContEA 的训练时间显着减少，这显示了其在处理连续实体对齐任务方面的部分优势。

4.5 Further Analysis

合并实体名称。 在这里，我们探讨利用实体名称的优势。实际上，我们使用 fasttext 库来生成实体的名称嵌入。由于 fasttext 的原始词嵌入维度为 300，为了使嵌入空间可扩展，我们使用官方降维器将维度降低到 100。此外，我们还引入了 Google Translate (G.T.) 作为竞争方法。对于跨语言数据集，我们首先将两个知识图谱中的实体翻译成同一种语言（英语或非英语），然后使用 Levenshtein 距离（语言学中流行的测量方法 和本体匹配 来计算名称相似度）。稍后还使用双向最近邻搜索来获得预测的可信实体对齐，将其与黄金测试集进行比较以计算 $P$、$R$ 和 $F1$ 分数。我们在表 6 中列出了 $F1$ 结果。通过利用名称属性，ContEA (fasttext) 的性能大幅优于 ContEA。随着时间的推移，谷歌翻译提供了令人满意且强大的性能，正如预期的那样强大。它的性能更稳定，对 KG 的大小不太敏感，在三个数据集的大多数快照上（第一个快照除外），其表现优于 ContEA（fasttext）。

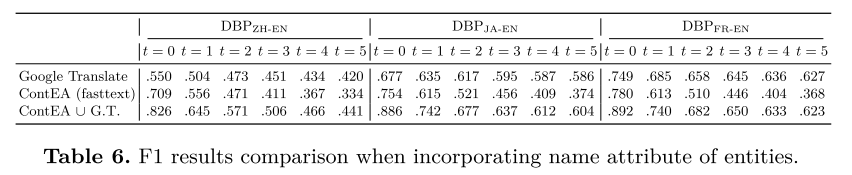
我们进一步探索 ContEA 和 Google Translate 的结合。为此，我们在搜索从一个 KG 到另一个 KG 的最近邻居时组合它们的预测对齐，然后采用双向交集来获得最终的组合预测对齐。这种组合的结果显示在最后一行。我们可以看到，在三个数据集的几乎所有快照中，它们的组合都优于 Google Translate 和 ContEA。我们相信，当 Google 翻译无法对齐实体时，ContEA 可以成为一个实用的替代方案。

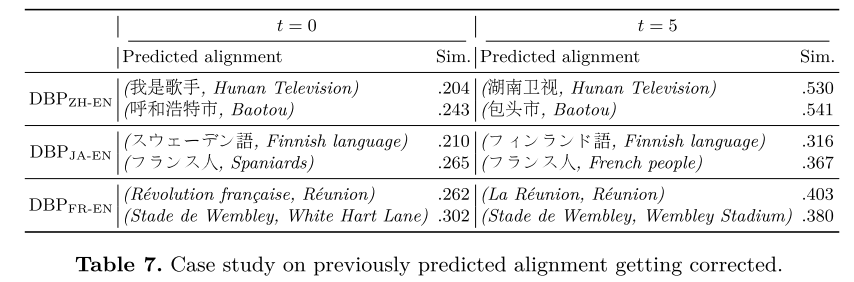
纠正先前对齐的案例研究。 最后，我们在表7中提供了几个关于先前预测的对齐在以后的精调过程中得到纠正的案例。我们保存预测的比对及其在时间 $t=0$和 $t=5$的相似性分数，并将每次涉及相同实体的两个比对对并列在一起。我们手动检查并置列表，并注意到，在 $t=0$处的预测对齐通常是不正确的，具有较小的相似性分数，而在$t=5$处的它们的对应物是正确的，具有较高的相似性分数。这表明了ContEA的自我纠正能力。同时，在$t=0$处错误预测的对准中的两个实体并非完全无关。例如，在$DB{P}_{FR-EN}$数据集的第二个案例中，温布利体育场和白鹿巷都是伦敦的体育场。在$DB{P}_{ZH-EN}$数据集的第一个案例中，我是歌手是湖南卫视制作的一档热门电视节目。在$DB{P}_{JA-EN}$数据集的第一个例子中，スウェーデン語表示瑞典语(瑞典和芬兰是两个相邻的北欧国家)。这给了一个有趣的洞察力，让我们了解ContEA如何预测实体对齐，但略有不准确。

5 Related Work

静态实体对齐。 大多数现有的基于嵌入的实体对齐方法都关注静态知识图谱。根据 KG 编码器的技术，它们通常可以分为两类：基于翻译的 和基于 GNN 的。前一类采用基于翻译的知识图谱嵌入（KGE）技术来嵌入实体，并基于预对齐的实体对将跨图实体映射到统一空间。基于 GNN 的实体对齐方法的编码器学习共享邻域聚合器以将实体嵌入到不同的 KG 中。近年来，它们获得了压倒性的流行，因为它们具有使用实体周围的子图而不是单个三元组来捕获结构信息的强大能力。有关更多详细信息，有几项调查（A comprehensive survey of entity alignment for knowledge graphs.和A benchmarking study of embedding-based entity alignment for knowledge graphs.）全面总结了最新进展。

动态实体对齐。 据我们所知，DINGAL是唯一解决知识图谱动态的实体对齐方法。在其动态场景中，新的三元组被添加到 KG 中，并且与这些新实体一起提供新的已知对齐。他们的工作中还提出了一种名为 DINGAL-O 的 DINGAL 变体，用于处理与我们类似的环境，其中预先已知的对齐不会增长。 DINGAL-O 是一种归纳方法，利用先前学习的模型参数来预测新的对齐方式。特别是，他们使用名称属性来生成用于实体初始化的词嵌入。

归纳知识图嵌入。 动态 KG 嵌入的研究多年来引起了广泛的关注。在 GNN 的支持下，提出了许多用于 KG 补全的归纳嵌入方法来生成新实体的嵌入。早期的归纳方法要么专注于半归纳设置，其中新实体连接到现有 KG 并在新实体和现有实体之间进行推理，要么专注于全归纳设置，其中新实体形成独立图并进行推理,新实体之间的推论。后来的归纳法打算解决这两种情况。同时，一些归纳知识图谱嵌入方法专注于特殊任务，例如小样本学习和超关系知识图谱补全。具体来说，作为第一个归纳 KG 嵌入方法，MEAN通过简单地对相邻实体关系对的信息进行均值池学习来使用其邻居来表示实体。LAN通过在池化过程中结合对实体关系对的基于规则的注意力和基于 GNN 的注意力来改进 MEAN。

6 Conclusion and Future Work

在本文中，考虑到现实世界知识图谱的增长性质，我们重点关注两个图都在增长的实体对齐场景，并解决名为连续实体对齐的新任务。我们提出了一种新方法 ContEA 作为该任务的解决方案。此外，我们构建了三个数据集来模拟场景并进行广泛的实验。实验结果表明，ContEA 相对于一系列再训练和归纳基线在有效性和效率方面具有优越性。对于未来的工作，当前提案有许多有希望的改进和扩展。关于设置，未来的研究可以考虑更复杂的场景，例如添加新关系、添加新的已知对齐方式，甚至删除实体和三元组。就方法而言，需要更可靠、更全面的值得信赖的对齐更新策略来处理复杂的对齐冲突情况。

论文原文：

https://arxiv.org/pdf/2207.11436.pdf

GitHub仓库：

https://github.com/nju-websoft/ContEA