计算机视觉——图像金字塔理解与代码示例

news2024/11/19 23:22:26

图像金字塔

有时为了在图像中检测一个物体（例如人脸、汽车或其他类似的物体），需要调整图像的大小或对图像进行子采样，并进行进一步的分析。在这种情况下，会保持一组具有不同分辨率的同一图像。称这种集合为图像金字塔。之所以称之为金字塔，是因为当按分辨率降序排列这些图像时，会形成一个以正方形为底的金字塔形状。下面的图片可以帮助你更详细地理解这个概念。
在这里插入图片描述
新层的面积将是下面层的1/4。如果底层图像（高分辨率或第0层）的大小是M x N，那么它上面的层的大小将是(M/2 x N/2)。其中图层越高，尺寸越小。
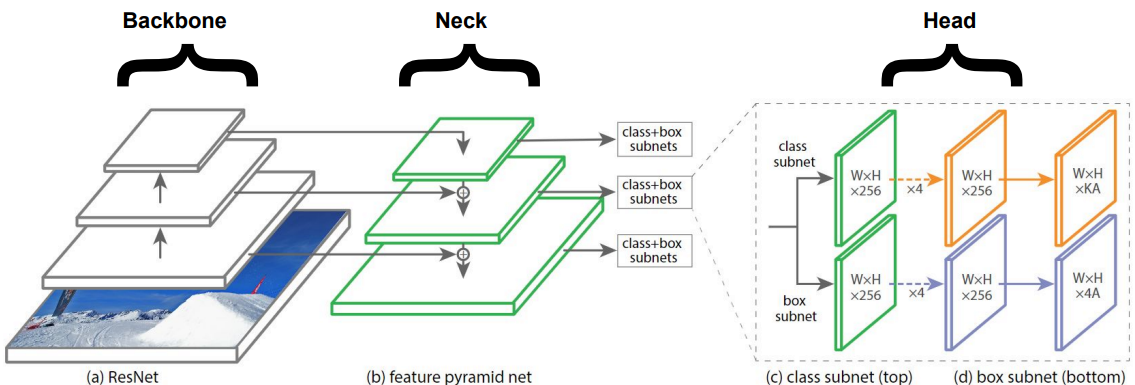
在一些著名的CNN神经网络中(如ResNet、YOLO、SSD等)，它们都使用了图像金字塔获取输入图像的特征。
在这里插入图片描述

高斯金字塔

高斯金字塔是SIFT算法中引入的概念。实际上，高斯金字塔并不是一个金字塔，而是由多个组（Octave）金字塔组成，每个组金字塔包含多个层（Interval）。

构建高斯金字塔的过程如下：

首先，将原始图像放大一倍，作为高斯金字塔的第一组的第一层。然后，对第一组的第一层图像进行高斯平滑（也称为高斯滤波），得到第一组金字塔的第二层。高斯卷积函数如下所示：

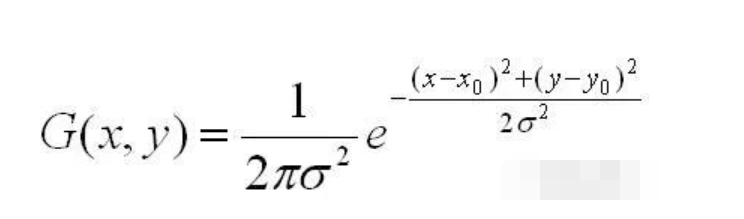
在这里插入图片描述

在SIFT算法中，参数σ取固定值1.6。

接下来，将σ乘以一个比例系数k，得到新的平滑因子σ= k * σ，然后使用该因子对第一组的第二层图像进行平滑处理，得到第一组的第三层。
重复以上步骤，直到得到L层图像。在同一组内，每层图像的尺寸相同，但平滑系数不同。它们的平滑系数分别为：0，σ，kσ，k^2σ，k3σ，……，k^(L-2)σ。
将第一组的倒数第三层图像进行比例因子为2的降采样，得到第二组的第一层。然后对第二组的第一层图像进行σ的高斯平滑处理，得到第二组的第二层，类似于步骤2。重复此过程，得到第二组的L层图像。在同一组内，它们的尺寸相同，但在不同组之间，第二组的图像尺寸是第一组图像尺寸的一半。

通过反复执行以上步骤，可以得到O组金字塔，每组包含L层，共计O*L个图像。这些图像一起构成了高斯金字塔。

在同一组内，不同层图像的尺寸相同，后一层图像的平滑系数是前一层图像平滑系数的k倍。在不同组之间，后一组的第一个图像是前一组倒数第三个图像的二分之一采样，尺寸是前一组的一半。

缩减或下采样

高斯金字塔中的缩减操作是根据下面给出的关系进行的。
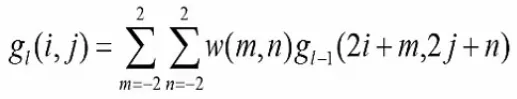
在这里插入图片描述
这里的l代表层级，w(m,n)是窗口函数（高斯）。缩减操作与卷积操作的唯一区别是，在卷积操作中，步长值为1，而在缩减操作中步长值为2。用高斯掩模与每一行和每一列交替进行卷积。

window=5
offset= window//2
gwindow =gkern(window,1.4)
row,col = gray_img.shape
if row%2==0:
    h = row-offset
else:
    h = row-offset-1
if col%2==0:
    w = row-offset
else:
    w = row-offset-1
nextLevel= np.zeros((w//2-1,h//2-1))
for i in range(2, w):
    for j in range(2, h):
        if j%2==0 and i%2==0:
            patch = gray_img[i-offset:i+offset+1,j-offset:j+offset+1]
            psum= np.dot(patch,gwindow).sum()
            nextLevel[(i//2)-1,(j//2)-1] = psum

opencv 实现

lowResImage = cv2.pyrDown(highResImage)

扩展或上采样

高斯金字塔中的扩展操作是根据下面给出的关系进行的。为了更清楚地理解上面的关系，让我们在一维情况下展开上面的公式。
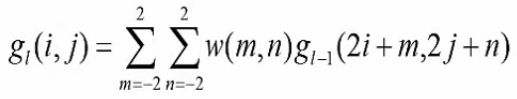
在这里插入图片描述
上面的公式中的非整数值最终将被消除，最终公式将只有三个项。

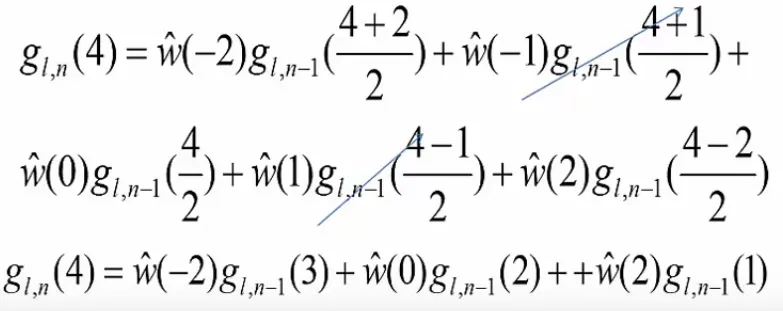
上面的图片中的a、b、c、d和e项是一维中的高斯权重。在扩展操作中，新像素是通过不同的高斯权重组合从旧像素创建的。
在这里插入图片描述

highResImage = cv2.pyrUp(lowResImage)

拉普拉斯金字塔

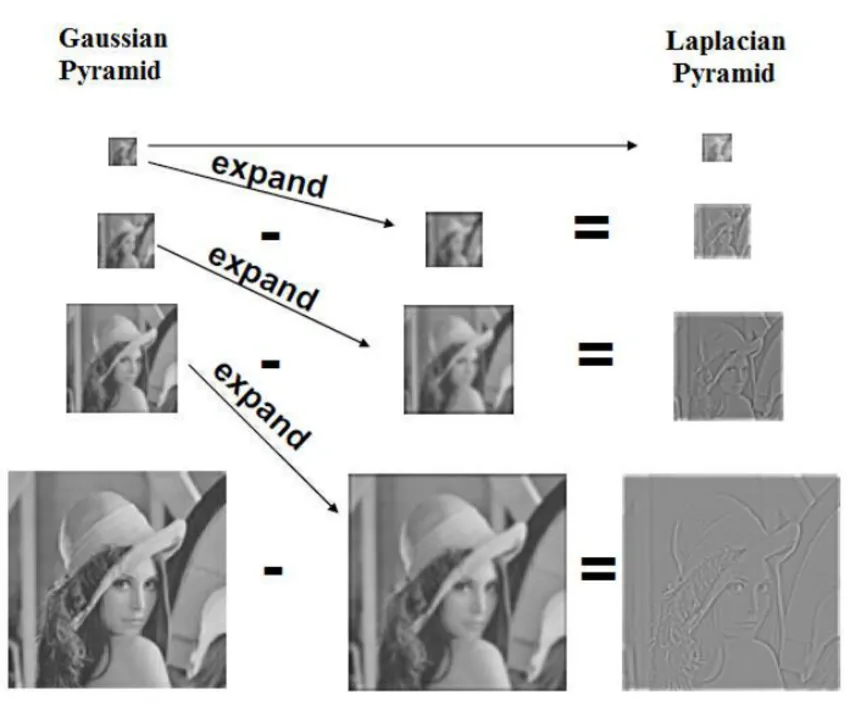
在这里插入图片描述
在高斯金字塔中，首先对图像应用高斯模糊，然后进行子采样以降低分辨率。这一过程在每个后续层级上重复进行，从而构建出一个由多个分辨率逐渐减小的图像层组成的金字塔结构。

而在拉普拉斯金字塔中，首先创建一个高斯金字塔，然后通过对每个高斯层级的应用拉普拉斯算子来构建。拉普拉斯算子，也就是拉普拉斯-高斯（LoG）算子，用于突出图像中的边缘和高频细节。这与Marr-Hildreth边缘检测器中使用的概念相似，该检测器利用LoG来识别图像中的边缘。

实际上，拉普拉斯金字塔是通过从高斯金字塔的每个层级中减去其下一层级上采样后的图像来创建的。这个过程在下面的公式中有所体现：

$L_{i} = G_{i} - upsample(G_{i+1})$

其中 $L_{i}$ 是拉普拉斯金字塔的第 $i$ 层， $G_{i}$ 是高斯金字塔的第 $i$ 层， $u p s am pl e$ 是上采样操作。

通过这种方法，可以生成拉普拉斯金字塔的每一层，从而捕获图像的不同尺度的细节信息。这在图像处理和计算机视觉中非常有用，尤其是在需要对图像进行多尺度分析的应用中，如图像融合、纹理分析和特征提取等。

OpenCV代码实现

import cv2
import numpy as np

def laplacian_pyramid(image, levels):
    pyramid = [image]
    for _ in range(levels):
        image = cv2.GaussianBlur(image, (5, 5), 0)
        downsampled = cv2.pyrDown(image)
        expanded = cv2.pyrUp(downsampled)
        diff = cv2.subtract(image, expanded)
        pyramid.append(diff)
        image = downsampled
    return pyramid

# Example usage
image = cv2.imread('input_image.jpg', cv2.IMREAD_GRAYSCALE)
levels = 4
laplacian_pyr = laplacian_pyramid(image, levels)