主要是我自己刷题的一些记录过程。如果有错可以指出哦,大家一起进步。
转载代码随想录
原文链接:
代码随想录
leetcode链接:654. 最大二叉树
题目:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例:
示例 1:
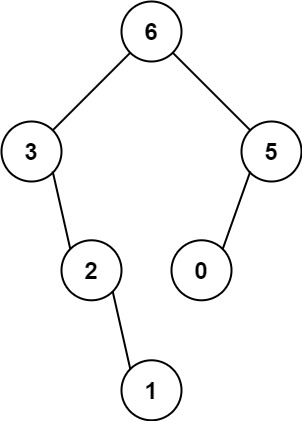
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:
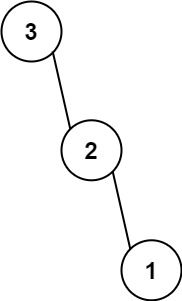
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
思路:
最大二叉树的构建过程如下:
 构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
确定递归函数的参数和返回值
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
代码如下:
TreeNode* constructMaximumBinaryTree(vector<int>& nums)
确定终止条件
题目中说了输入的数组大小一定是大于等于1的,所以我们不用考虑小于1的情况,那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。
那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
代码如下:
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
node->val = nums[0];
return node;
}
确定单层递归的逻辑
这里有三步工作
1.先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组。
代码如下:
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > maxValue) {
maxValue = nums[i];
maxValueIndex = i;
}
}
TreeNode* node = new TreeNode(0);
node->val = maxValue;
2.最大值所在的下标左区间 构造左子树
这里要判断maxValueIndex > 0,因为要保证左区间至少有一个数值。
代码如下:
if (maxValueIndex > 0) {
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
3.最大值所在的下标右区间 构造右子树
判断maxValueIndex < (nums.size() - 1),确保右区间至少有一个数值。
代码如下:
if (maxValueIndex < (nums.size() - 1)) {
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
}
这样我们就分析完了,整体代码如下:(详细注释)
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
node->val = nums[0];
return node;
}
// 找到数组中最大的值和对应的下标
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > maxValue) {
maxValue = nums[i];
maxValueIndex = i;
}
}
node->val = maxValue;
// 最大值所在的下标左区间 构造左子树
if (maxValueIndex > 0) {
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
// 最大值所在的下标右区间 构造右子树
if (maxValueIndex < (nums.size() - 1)) {
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
}
return node;
}
};
以上代码比较冗余,效率也不高,每次还要切割的时候每次都要定义新的vector(也就是数组),但逻辑比较清晰。
和文章二叉树:构造二叉树登场!中一样的优化思路,就是每次分隔不用定义新的数组,而是通过下标索引直接在原数组上操作。
优化后代码如下:
class Solution {
private:
// 在左闭右开区间[left, right),构造二叉树
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left >= right) return nullptr;
// 分割点下标:maxValueIndex
int maxValueIndex = left;
for (int i = left + 1; i < right; ++i) {
if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
}
TreeNode* root = new TreeNode(nums[maxValueIndex]);
// 左闭右开:[left, maxValueIndex)
root->left = traversal(nums, left, maxValueIndex);
// 左闭右开:[maxValueIndex + 1, right)
root->right = traversal(nums, maxValueIndex + 1, right);
return root;
}
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums, 0, nums.size());
}
};
拓展
可以发现上面的代码看上去简洁一些,主要是因为第二版其实是允许空节点进入递归,所以不用在递归的时候加判断节点是否为空
第一版递归过程:(加了if判断,为了不让空节点进入递归)
if (maxValueIndex > 0) { // 这里加了判断是为了不让空节点进入递归
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
if (maxValueIndex < (nums.size() - 1)) { // 这里加了判断是为了不让空节点进入递归
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
}
第二版递归过程: (如下代码就没有加if判断)
root->left = traversal(nums, left, maxValueIndex);
root->right = traversal(nums, maxValueIndex + 1, right);
第二版代码是允许空节点进入递归,所以没有加if判断,当然终止条件也要有相应的改变。
第一版终止条件,是遇到叶子节点就终止,因为空节点不会进入递归。
第二版相应的终止条件,是遇到空节点,也就是数组区间为0,就终止了。
总结
这道题目其实和 二叉树:构造二叉树登场!是一个思路,比二叉树:构造二叉树登场!还简单一些。
注意类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
一些同学也会疑惑,什么时候递归函数前面加if,什么时候不加if,这个问题我在最后也给出了解释。
其实就是不同代码风格的实现,一般情况来说:如果让空节点(空指针)进入递归,就不加if,如果不让空节点进入递归,就加if限制一下, 终止条件也会相应的调整。
自己的代码
我自己提交了3份代码,对比了一下
1.时间击败5.42%
class Solution {
public:
int findMax(const vector<int>& nums) {
int maxV = INT_MIN;
for (const auto& num : nums) {
maxV = maxV > num ? maxV : num;
}
return maxV;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (!nums.size()) return nullptr;
if (nums.size()==1 ) return new TreeNode(nums[0]);
int maxVal = findMax(nums);
unordered_map<int, int> hashMap;
int i = 0;
for (const auto& num : nums) {
hashMap[num]=i++;
}
TreeNode* root = new TreeNode(maxVal);
vector<int> leftVec{ nums.begin(), nums.begin()+ hashMap[maxVal] }; //左闭右开
root->left = constructMaximumBinaryTree(leftVec);
vector<int> rightVec{ nums.begin() + hashMap[maxVal]+1, nums.end() }; //左闭右开
root->right = constructMaximumBinaryTree(rightVec);
return root;
}
};
2.时间击败84.40%
class Solution {
public:
TreeNode* helpFunc(int leftIndex, int rightIndex, vector<int>& nums) {
if (leftIndex== rightIndex) return nullptr;
if (leftIndex+1 == rightIndex) return new TreeNode(nums[leftIndex]); //只有一个元素
int maxVal = -1;
int index = -1;
for (int i = leftIndex; i < rightIndex; i++) { //至少有一个元素
if (maxVal < nums[i]) {
maxVal = nums[i];
index = i;
}
}
TreeNode* root = new TreeNode(maxVal);
root->left = helpFunc(leftIndex, index, nums);//左闭右开 特殊情况[0,0) 即没有元素。
root->right = helpFunc(index+1, rightIndex, nums);//左闭右开 特殊情况[0,0) 即没有元素。
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.size() == 1) return new TreeNode(nums[0]);
return helpFunc(0, nums.size(), nums);//左闭右开
}
};
3.时间击败43.11%
class Solution {
public:
unordered_map<int, int>hashMap;
TreeNode* helpFunc(int leftIndex, int rightIndex, vector<int>& nums) {
if (leftIndex== rightIndex) return nullptr;
if (leftIndex+1 == rightIndex) return new TreeNode(nums[leftIndex]); //只有一个元素
int maxVal = -1;
for (int i = leftIndex; i < rightIndex; i++) { //至少有一个元素
maxVal = maxVal > nums[i] ? maxVal : nums[i];
}
int index = hashMap[maxVal];
TreeNode* root = new TreeNode(maxVal);
root->left = helpFunc(leftIndex, index, nums);//左闭右开 特殊情况[0,0) 即没有元素。
root->right = helpFunc(index+1, rightIndex, nums);//左闭右开 特殊情况[0,0) 即没有元素。
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.size() == 1) return new TreeNode(nums[0]);
for (int i = 0; i < nums.size(); i++) {
hashMap[nums[i]] = i;
}
return helpFunc(0, nums.size(), nums);//左闭右开
}
};
感觉这3份代码各有特色吧,其实还有一种更高效的方法我没太搞懂。下次再来看。下面是力扣官方题解。
作者:力扣官方题解
链接:https://leetcode.cn/problems/maximum-binary-tree/solutions/1759348/zui-da-er-cha-shu-by-leetcode-solution-lbeo/
来源:力扣(LeetCode)
方法二:单调栈
思路与算法
我们可以将题目中构造树的过程等价转换为下面的构造过程:
初始时,我们只有一个根节点,其中存储了整个数组;
在每一步操作中,我们可以「任选」一个存储了超过一个数的节点,找出其中的最大值并存储在该节点。最大值左侧的数组部分下放到该节点的左子节点,右侧的数组部分下放到该节点的右子节点;
如果所有的节点都恰好存储了一个数,那么构造结束。
由于最终构造出的是一棵树,因此无需按照题目的要求「递归」地进行构造,而是每次可以「任选」一个节点进行构造。这里可以类比一棵树的「深度优先搜索」和「广度优先搜索」,二者都可以起到遍历整棵树的效果。
既然可以任意进行选择,那么我们不妨每次选择数组中最大值最大的那个节点进行构造。这样一来,我们就可以保证按照数组中元素降序排序的顺序依次构造每个节点。因此:
当我们选择的节点中数组的最大值为 nums[i]时,所有大于 nums[i]的元素已经被构造过(即被单独放入某一个节点中),所有小于 nums[i]的元素还没有被构造过。
这就说明:
在最终构造出的树上,以 nums[i]为根节点的子树,在原数组中对应的区间,左边界为 nums[i]左侧第一个比它大的元素所在的位置,右边界为 nums[i]右侧第一个比它大的元素所在的位置。左右边界均为开边界。
如果某一侧边界不存在,则那一侧边界为数组的边界。如果两侧边界均不存在,说明其为最大值,即根节点。
并且:
nums[i] 的父结点是两个边界中较小的那个元素对应的节点。
因此,我们的任务变为:找出每一个元素左侧和右侧第一个比它大的元素所在的位置。这就是一个经典的单调栈问题了,可以参考 503. 下一个更大元素 II。如果左侧的元素较小,那么该元素就是左侧元素的右子节点;如果右侧的元素较小,那么该元素就是右侧元素的左子节点。
代码
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
int n = nums.size();
vector<int> stk;
vector<int> left(n, -1), right(n, -1);
vector<TreeNode*> tree(n);
for (int i = 0; i < n; ++i) {
tree[i] = new TreeNode(nums[i]);
while (!stk.empty() && nums[i] > nums[stk.back()]) {
right[stk.back()] = i;
stk.pop_back();
}
if (!stk.empty()) {
left[i] = stk.back();
}
stk.push_back(i);
}
TreeNode* root = nullptr;
for (int i = 0; i < n; ++i) {
if (left[i] == -1 && right[i] == -1) {
root = tree[i];
}
else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) {
tree[left[i]]->right = tree[i];
}
else {
tree[right[i]]->left = tree[i];
}
}
return root;
}
};
我们还可以把最后构造树的过程放进单调栈求解的步骤中,省去用来存储左右边界的数组。下面的代码理解起来较为困难,同一个节点的左右子树会被多次赋值,读者可以仔细品味其妙处所在。
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
int n = nums.size();
vector<int> stk;
vector<TreeNode*> tree(n);
for (int i = 0; i < n; ++i) {
tree[i] = new TreeNode(nums[i]);
while (!stk.empty() && nums[i] > nums[stk.back()]) {
tree[i]->left = tree[stk.back()];
stk.pop_back();
}
if (!stk.empty()) {
tree[stk.back()]->right = tree[i];
}
stk.push_back(i);
}
return tree[stk[0]];
}
};
复杂度分析
时间复杂度:O(n),其中 nnn 是数组 nums\textit{nums}nums 的长度。单调栈求解左右边界和构造树均需要 O(n)的时间。
空间复杂度:O(n),即为单调栈和数组 tree 需要使用的空间。