【动态规划】【01背包问题】
- 解法 二维dp数组01背包
- 解法 一维dp数组(滚动数组)01背包
---------------🎈🎈题目链接🎈🎈-------------------
解法 二维dp数组01背包
😒: 我的代码实现============>
动规五部曲
✒️确定dp数组以及下标的含义
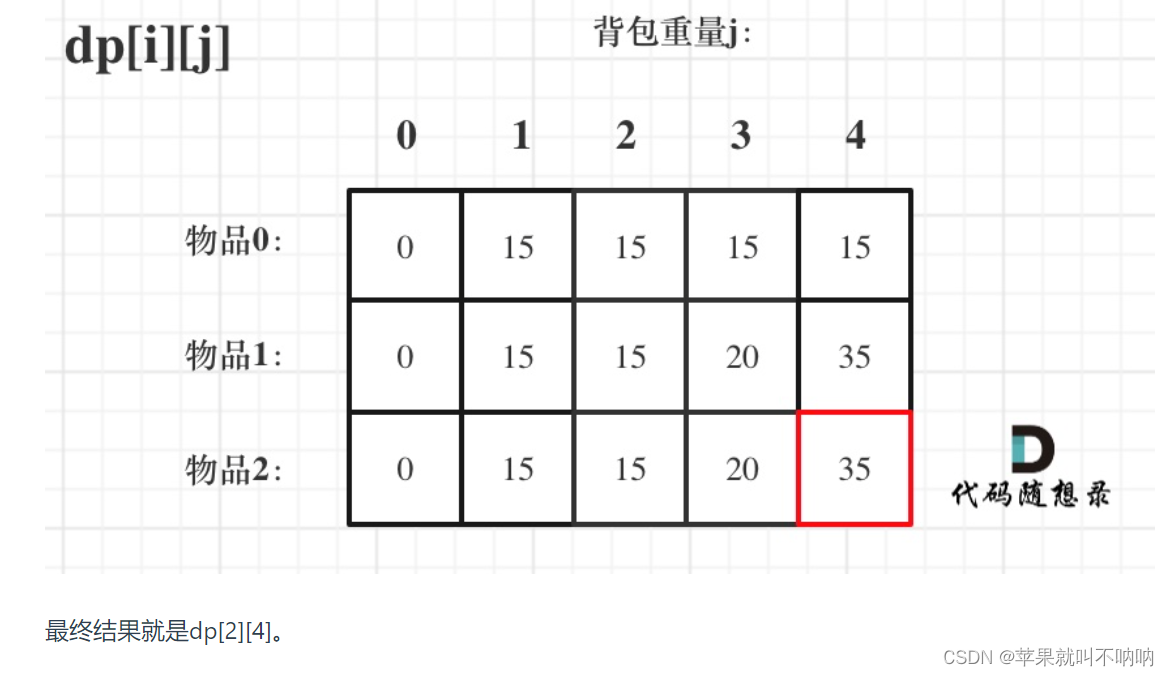
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
✒️确定递推公式
不放物品i:由
dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,
那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
✒️dp数组初始化
空间为0时,所有物品都放不进去,价值都为0
物品0的重量超过书包重量时,放不进去,价值为0。超过后就可以放入,此时价值为物品0的价值,value[0]
✒️确定遍历顺序
先遍历背包和先遍历物品都可以
✒️举例推导dp数组
时间复杂度O(N)
空间复杂度O(N)
📘代码
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner scanner = new Scanner(System.in);
int goodscount = scanner.nextInt(); //物品个数
int bagsize = scanner.nextInt(); //书包大小
int[] space = new int[goodscount];
int[] value = new int[goodscount];
scanner.nextLine();
for(int i = 0; i < goodscount ; i++){
space[i] = scanner.nextInt();
}
scanner.nextLine();
for(int j = 0; j < goodscount ; j++){
value[j] = scanner.nextInt();
}
// dp[i][j]:代表0-i号物品 放到j大小的背包中 的最大价值
int[][] dp = new int[goodscount][bagsize+1];
//初始化dp数组
// 背包重量为0的时候,所有物品对应的价值均为0
for(int i = 0; i < goodscount; i++){
dp[i][0] = 0;
}
//物品0:只有在其重量小于等于背包容量 bagsize 时,对应的dp[i][j]才等于其价值value[0],否则就都是0
for(int i = space[0]; i <= bagsize; i++){
dp[0][i] = value[0];
}
// 递推表达式:dp[i][j] = max( dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] )
for(int i = 1; i < goodscount; i++){
for(int j = 1; j <= bagsize; j++){
if(j<space[i]){
// 当当前书包容量小于物品i重量space[i]时 就放不进去
// 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
dp[i][j] = dp[i-1][j];
}
else{
// 当前背包的容量可以放下物品i,那么此时分两种情况:
// 1、不放物品i
// 2、放物品i
// 比较这两种情况下,哪种背包中物品的最大价值最大
dp[i][j] = Math.max( dp[i-1][j] , dp[i-1][j-space[i]] + value[i] );
}
}
}
System.out.println(dp[goodscount-1][bagsize]);
}
}
解法 一维dp数组(滚动数组)01背包
😒: 我的代码实现============>
动规五部曲
✒️确定dp数组以及下标的含义
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。。
✒️确定递推公式
不放物品i:dp[j]
放物品i:dp[j - weight[i]] + value[i]
所以递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
✒️dp数组初始化
空间为0时,所有物品都放不进去,值都为0:dp[0] = 0
其他下初始化:dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
✒️确定遍历顺序
先正向遍历物品
再反向遍历背包容量
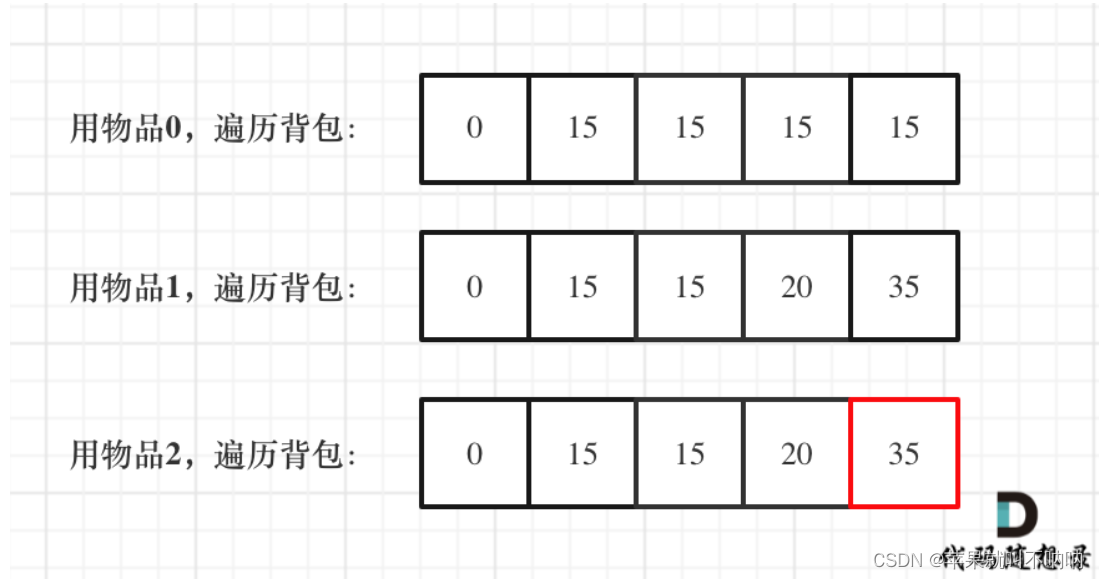
✒️举例推导dp数组
📘代码
package ACM;
import java.util.*;
public class test{
public static void main (String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
testWeightBagProblem(weight, value, bagWeight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
// 【dp[j]:代表背包容量为j时候 能获得的最大价值】
int[] dp = new int[bagWeight+1];
//【初始化dp数组】
// 背包重量为0的时候,价值为0,其余初始化均为0
dp[0] = 0;
// 二维递推表达式:dp[i][j] = max( dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] )
// 一维滚动数组:dp[j] = max( dp[j], dp[j-weight[i]]+value[i] )
// 【遍历顺序:正序遍历物品i + 倒序遍历背包容量j】
// 用物品0遍历背包 0 15 15 15 15
// 物品0,背包容量为bagWight=4时,能获得的最大价值 dp[4] = max(不放物品0:0, 放物品0:dp[4-weight[0]] + value[0]) = 15
// 物品0,背包容量为3时,能获得的最大价值 15 dp[3] = max(0, dp[3-weight[0]] + value[0]) = 15
// 物品0,背包容量为2时,能获得的最大价值 15 dp[2] = max(0, dp[2-weight[0]] + value[0]) = 15
// 物品0,背包容量为1时,能获得的最大价值 15 dp[1] = max(0, dp[1-weight[0]] + value[0]) = 15
// 物品0,背包容量为0时,能获得的最大价值 0 0
// 用物品1遍历背包 0 15 15 20 35
// 物品1,背包容量为bagWight=4时,能获得的最大价值 dp[4] = max(dp[4], dp[4-weight[1]] + value[1]) = max(15, 15+20) = 35
// 物品1,背包容量为3时,能获得的最大价值 15 dp[3] = max(dp[3], dp[3-weight[1]] + value[1]) = max(15, 0+20) = 20
// 物品1,背包容量为2时,能获得的最大价值 15 dp[2] = max(dp[2], 物品1放不下:0) = max(15, 0) = 15
// 物品1,背包容量为1时,能获得的最大价值 15 dp[1] = max(dp[1], 物品1放不下:0) = max(15, 0) = 15
// 物品1,背包容量为0时,能获得的最大价值 0 0
// 用物品2遍历背包
// ...
// 物品weight.length-1
for(int i = 0; i < weight.length; i++){ // 正向遍历物品i
for(int j = bagWeight; j >= weight[i]; j--){ // 反向遍历背包容量j
dp[j] = Math.max(dp[j] , dp[j-weight[i]]+value[i]);
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
}