图论(Graph theory)

抽象数据结构类型

Graphic操作接口

操作接口	功能描述	操作接口	功能描述
e()	获取图的总边数	n()	顶点的总数
exits(v,u)	判断v,u两个顶点是否存在边	insert(v)	在顶点集 V 中插入新顶点 v
remove(v,u)	删除从v 到u的关联边	remove(v)	将顶点 v 从顶点集中删除
type(v,u)	边所属的类型(主要用于遍历树~)	inDegree(v) outDegree(v)	顶点 v的入度、出度
edge(v,u)	该边所对应的数据域	firstNbr(v)	顶点 v的首个邻接顶点
weight(v,u)	该边所对应的权重	nextNbr(v, u)	在 v的邻接顶点中， u 的后继
		status(v)	顶点的状态
		parent(v)	顶点 v 在遍历树中的父节点

Graphic抽象数据结构设计

🎈 顶点类:

// 节点简化封装
template<typename Tv> 
struct Vertex
{
	// 顶点val
	Tv _data;
	// 入度、出度、 父节点
	int _inDegree, _outDegree, _parent;
	VStatus _stat;
		// 构造新节点
	Vertex(const Tv& data = (Tv)0) :_data(data), _inDegree(0), _outDegree(0), _stat(UNDISCOVERED), _parent(-1){}
};

其包含该顶点表示的数据域，以及顶点状态、入、出度数量等

🎈 关联边类:

// 边对象优化
template<typename Te>
struct Edge
{
	//数据、权重、类型
	Te _data;
	int _weight;
	EType _type;
	Edge(const Te& data, int weight) :_data(data), _weight(weight), _type(UNDETERMINED){}
};

关联边最直接的表现是两个顶点的连接情况~ 但在有些应用场景中，需要关联边的存储记录更详尽的数据，例如：从四川开往北京的火车中，从成都 - 北京是一条线，从成都-西安-太原-北京又是另一条路线。这条线可以有这些数据：路程长度、价格、时间长短，这就是关联便所能表示的数据域。

🎈 图类:

template<typename Tv,typename Te>
class Graph
{
protected:
	int _n = 0;  //顶点总数
	int _e = 0;	 //边总数

public:
	// 顶点
	virtual Tv& vertex(int) = 0;					 // 顶点v癿数据（诠顶点癿确存在）
	virtual int inDegree(int) = 0;					 // 顶点v癿入度（诠顶点癿确存在）
	virtual int outDegree(int) = 0;					 //顶点v癿出度（诠顶点癿确存在）
	virtual VStatus& status(int) = 0;				 //顶点v癿状态
	virtual int& parent(int) = 0;					 //顶点v在遍历树中癿父亲

	virtual int insert(Tv const&) = 0;				 // 插入顶点，返回编号
	virtual Tv remove(int) = 0;						 // 初除顶点及其关联边，返回顶点信息
	virtual int firstNbr(int) = 0;					 //顶点v癿首个邻接顶点
	virtual int nextNbr(int, int) = 0;				 //顶点v的（相对亍顶点j癿）下一邻接顶点

	// 边
	virtual bool exists(int, int) = 0;				    //边(v, u)是否存在
	virtual void insert(Te const&, int, int, int) = 0;  //在顶点v和u乀间揑入权重为w癿边e
	virtual Te remove(int, int) = 0;					//初除顶点v和u之间的边e，返回该边信息
	virtual EType& type(int, int) = 0;					//边(v, u)的类型
	virtual Te& edge(int, int) = 0;						//边(v, u)的数据 
	virtual int& weight(int, int) = 0;					//边(v, u) 的权重

    // ... 在这里我只列举一部分出来
};

这里选择的是模板类的设计，是为了兼容不同图的存储方式。其中，声明大量的纯虚函数，其本质就是为了让子类全然重写这些函数。

🎃 邻接矩阵

// 基类进行重写
template<typename Tv,typename Te>
class GraphMatrix :public Graph<Tv, Te>
{
private:
	// 数据抽象管理  —— 邻接表
	vector<Vertex<Tv>> _V;   // 顶点集合 —— 多少个顶点被插入
	vector<vector<Edge<Te>*>> _E; // 边集合

    // ...  完成 虚函数重写~
}

接口函数实现:

{
	// 顶点操作
	virtual Tv& vertex(int i) { return _V[i]._data; }
	virtual int inDegree(int i) { return _V[i].__inDegree; }
	virtual int outDegree(int i) { return _V[i]._outDegree; }
	virtual VStatus& status(int i) { return _V[i]._status; }
	virtual int& parent(int i) { return _V[i]._parent; }
	virtual int firstNbr(int i) { return nextNbr(i, _n); }

    // 边的操作
	virtual EType& type(int i, int j) { return _E[i][j]->_type; }   // 边(i, j)的类型
	virtual Te& edge(int i, int j) { return _E[i][j]->_data; }	  //边(i, j)的数据
	virtual int& weight(int i, int j) { return _E[i][j]->_weight; } //边(i, j)的权重
	virtual bool exists(int i, int j)
	{
				// 保证不越界
		return ((i >= 0) && (i < _n) && (j >= 0) && (j < _n)) && _E[i][j] != nullptr;
	}

}

接口插入与删除的实现:

{
		// 顶点动态插入  返回的是插入节点的 迭代器
		virtual int insert(const Tv& vertex)
		{
			// 每个顶点新曾一列  —— 用于 关联这个新节点
			for (int j = 0;j < _nVertexs;++j) _E[j].insert(nullptr);
		
			// 创建该顶点 以及对应的 关联边默认为:nullptr
			//vector<Edge*> new_matrix(n, nullptr);
			//_E.push_back(new_matrix);
			++_nVertexs;
			_E.insert(_nVertexs, _nVertexs, (Edge<Te>*)nullptr);
			return _V.insert(Vertex<Tv>(vertex));
		}

		// 顶点移除 初除第i个顶点及其兲联边（0 <= i < n）
		virtual Tv remove(int i)
		{
			// 删除其所有的 入边
			// i -> j
			for (int j = 0;j < _nVertexs;++j)
				if (exists(i, j)) { delete _E[i][j]; _V[j]._inDegree--; }	// 当我们要删除某个顶点时，先将其边删除
 
			// 删除其所有的 出边
			// j -> i
			for (int j = 0;j < _nVertexs;++j)
				if (Edge<Te>* e = _E[j].erase(i)) { delete e; _V[j]._outDegree--; }

			// 移除边
			_E.erase(i);
			_nVertexs--;

			// 获取备份 + 从顶点集中移除
			Tv vbak = vertex(i);
			_V.erase(i);

			return vbak; // 返回被删除顶点的信息
		}
    
/
		// 边的动态操作 针对两点 之间的边操作~
		virtual void insert(const Te& edge,int w,int i,int j)  // 针对带 权值的边e
		{
			if (exists(i, j)) return; // 已经存在边 不能插入了~
			_E[i][j] = new Edge<Te>(edge, w);	// 创建新边
			++_eEdges;
			// 更新关联点的 出入度
			// [i,j]  i --> j
			_V[i]._outDegree++;
			_V[j]._inDegree++;
		}

		virtual Te remove(int i, int j)
		{
			Te ebak = edge(i, j);
			delete _E[i][j];
			_E[i][j] = nullptr;

			++_eEdges;
			_V[i]._outDegree--;
			_V[j]._inDegree--;
			return ebak;
		}
}

🎃 邻接表

关于邻接表如何进行的存储以及接口实现并不在此表述，只是稍微进行写一份伪代码~

	template<typename Tv, typename Te>
	class GraphTables :public Graph<Tv, Te>
	{
	private:
		vector<Vertex<Tv>> _V; // 顶点集合
		vector<Edge<Te>*> _tables; // 与顶点集合的下标对应 存储 真正的临界表~
		unordered_map<Vertex<Tv>,int> _tablesMap; // 这里我们采用哈希结构 快速找到与顶点V 相关联的边

	public:
		virtual int insert(const Tv& vertex)
		{
			++_n;
			// 直接入 顶点集合即可~ 
			return _V.insert(Vertex<Tv>(vertex));
		}

		virtual void insert(const Te& edge, int w, int i, int j)
		{
			if (exists(i, j)) return;
			Edge<Te>* new_edge = new Edge<Te>(edge, w);
			// 你要进入哪个表？
			int idx = _tablesMap[vertex(i, j)];
			// 进行头插
			new_edge->_next = _tables[idx];
			_tables[idx] = new_edge;
			
			int idx2 = _tablesMap[vertex(j, i)];
			_V[idx]._outDegree++;
			_V[idx]._inDegree++;
			++_e;
		}
        // .... and so on ....
	};

注: 这里的所有实现本身就是一份伪代码，只是具有部分参考意义~

图的搜索遍历

广度优先搜索

template<typename Tv, typename Te>
void Graph<Tv, Te>::bfs(int s)
{
	// 从每一个节点进行遍历~
	int v = s; // s: 0 ~ n
	do
	{
		if (status(v) == UNDISCOVERED) {
			// 该节点没有被遍历 进行BFS
			BFS(v);
		}
	} while (s != (v = (++v % n));	// 这里本质就是从第一个节点开始向后遍历~ 当v==n-1时 就会退出

	
}

template<typename Tv, typename Te>
void Graph<Tv, Te>::BFS(int v)
{
	// 引入辅助队列 进行层序遍历~
	queue<int> que;
	status(v) = DISCOVERED; // 标记v已经被访问
	while (!que.empty())
	{
		int front = que.front();
		que.pop();

		// firstNbr: u从n开始-- 直到找到 有关联的节点v
		// 否则返回 -1
		for (int u = firstNbr(front); -1 < u; u = nextNbr(front, u))
		{
			if (status(u) == UNDISCOVERED) {
				// 该顶点尚未被 发掘插入进队列
				status(u) = DISCOVERED;
				que.push(u);

				// 记录其他信息 这些步骤 对于简单的BFS或DFS可以不用
				parent(u) = v;
				type(v, u) = TREE;	// 引入树边拓展支撑树
			}
			else {
				type(v, u) = CROSS	// 该节点 跨边了
			}
		}
		status(front) = VISITED; // 该节点被访问了~
	}
}

"bfs()" 将所有存在于顶点集中的顶点挨个进行迭代，每个顶点是否需要进行“BFS()”的根据在于是否处于 "UNDISCOVERED".

“BFS()”的每一步迭代，都需要从队列que中取出当前的 “首顶点”v，再对其邻居u顶点逐一筛查 —— 如果是“UNDISCOVERED” 入队列，否则记录 “CROSS”状态(这个状态再当前不考虑)~

BFS()遍历结束后，所有访问过的顶点通过 parent[]指针依次联接，从整体上给出了原图某一连通或可达域的一棵遍历树。

深度优先搜索

template<typename Tv, typename Te>
void Graph<Tv, Te>::dfs(int s)
{
	int v = s; // s: 0 ~ n
	do
	{
		if (status(v) == UNDISCOVERED) {
			BFS(v);
		}
	} while (s != (v = (++v % n));
}

template<typename Tv, typename Te>
void Graph<Tv, Te>::DFS(int v)
{
	status(v) = DISCOVERED;  // 标记该 顶点已经被遍历
	for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u))
	{
		// 找到自己邻居顶点u
		switch (u)
		{
			case UNDISCOVERED:
				// u尚未被发现 就以它进行 拓展~
				type(v, u) = TREE;
				parent(u) = v;
				DFS(u);
				break;
			case DISCOVERED:
				// u尚未访问完毕 v是u的祖先节点~
				type(v, u) = BACKWARD;
				break;
			default:
				break;
		}
	}
	status(v) = VISITED; // 访问完毕~ ——> 该顶点的所有邻居顶点都完成了访问~
}

深度优先搜索dfs通常都是使用递归方法来实现的，每一递归实例中，都先将当前节点v标记为 “DISCOVERED”，再逐一核对其各邻居u的状态并做相应处理。待其所有邻居均已处理完毕之后，将顶点v置为VISITED（访问完毕）状态，便可回溯。

若顶点u尚处于UNDISCOVERED，归类(v,u)的父子关系后，继续以u作为首顶点进行遍历。

DFS(s)返回后，所有访问过的顶点通过parent[]指针依次联接从整体上给出了顶点s所属连通或可达分量的一棵遍历树。

注: 这里的讨论仅限于 ”无向图“

有关图的其他应用

拓扑排序

template <typename Tv, typename Te>
stack<Tv>* Graph<Tv, Te>::tSort(int s)
{
	// 用于记录 拓扑顺序
	stack<Tv>* st = new  stack<Tv>(); 
	// 我们用每个节点进行拓扑~
	do {
		if (UNDISCOVERED == status(v)) {
			if (!TSort(v, st)) {
				while (!st->empty())
					st->pop();
			}
		}
	}while (s != (v = (++v % n)));
	return st;
}

template <typename Tv, typename Te>
bool Graph<Tv, Te>::TSort(int v,stack<Tv>* st)
{
	// 枚举v所在的顶点
	for (int u = firstNbr(v), -1 < u;u = nextNbr(v, u))
	{
		switch (status(u))
		{
			case UNDISCOVERED:
				parent(u) = v;
				type(u, v) = TREE;
				// 继续以u进行 拓扑
				if (!TSort(u, st)) {
					return false;
				}
				break;
			case DISCOVERED:
				// 出现了指向前驱 顶点的指针
				type(v, u) = BACKWARD;
				return false;
			default:
				// visited
				return false;
		}
	}
	// 说明以该顶点进行拓扑是顺利的
	status(v) = VISITED;
	st->push(v);
	return true;
}

相对于标准的DFS搜索算法，这里增设了一个栈结构。一旦某个顶点被标记为VISITED状态，便随即令其入栈。如此，当搜索终止时，所有顶点即按照被访问完毕的次序，在栈中自顶向下而排列！

如果你感兴趣，可以试试这道考察图拓扑结构的题目: 课程表 ...

双连通域分解

template <typename Tv, typename Te>
void Graph<Tv, Te>::bcc(int s)
{
	int v = s;
	stack<int>* st = new stack<int>();
	do {
		if (UNDISCOVERED == status(v)) {
			BCC(v, st);
			// 访问完成
			st->pop();
		}
	} while (s != 0);
}
#define hca(x) (fTime(x)) // 利用此处闲置的fTime[]充当hca[]
template<typename Te,typename Tv>
void Graph<Te, Tv>::BCC(int v, stack<int>* st)
{
	// 标志更新
	status(v) = DISCOVERED;
	st->push(v);

	// 遍历邻里节点
	for (int u = firstNbr(v);u > -1;u = nextNbr(v, u))
	{
		switch (status(u))
		{
			case UNDISCOVERED:
				parent(u) = v;
				type(v, u) = TREE;
				BCC(u, st);
				if (hac(u) < dtime(v)) {
					// u遍历回来后 发现自己可以指向v的先祖节点 那么v压根不能称为关节点
					hca(v) = min(hca(v), hca(u));  // 进行更新v的先祖节点
				}
				else {
					// v 是关节点 
					while (v != st->top()) {
						st->pop();
					}
				}
				break;
			case DISCOVERED:
				type(v, u) = BACKWARD; // 表示u一定是v的 先祖先
				if (u != parent(v)) hac(v) = min(hca(v), dtime(u)); // 重新找先祖先
				break;
			default:
				// visiatd
				type(v, u) = (dtime(v) < dtime(u)) ? FOWARD : CROSS;
				break;
		}
	}
	status(v) = VISITED;
}

DFS搜索在顶点v的孩子u处返回之后，通过比较hca[u]与dTime[v]的大小，即可判断v是否关节点。通过比较hca[u]与dTime[v]，则说明u及其后代无法通过后向边与v的真祖先连通，故v为关节点。

既然栈S 存有搜索过的顶点，与该关节点相对应的双连通域内的顶点，此时都应集中存放于S顶部，故可依次弹出这些顶点。v本身必然最后弹出，作为多个连通域的联接枢纽，它应重新进栈，访问另一个连通域。

最小生成树

Edge类封装:

		struct Edge
		{
			size_t _srci;
			size_t _dsti;
			W _w;
			Edge(size_t srci, size_t dsti, const W& w)
				:_srci(srci)
				, _dsti(dsti)
				, _w(w)
			{}

			bool operator>(const Edge& e) const
			{
				return _w > e._w;
			}
		};

Kruskal算法：

		W Kruskal(Self& minTree)
		{
			// 初始化
			int n = _vertex.size();
			minTree._vertex = _vertex;
			minTree._tablemap = _tablemap;
			minTree._edges.resize(_edges.size());
			for (size_t i = 0;i < minTree._edges.size();++i)
				minTree._edges[i].resize(n, MAX_W);

			// 凭借优先级队列 选出权值最短的两条边
			priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
			for(int i=0;i<n;++i)
				for (int j = 0;j < n;++j)
				{
					if (i < j && _edges[i][j] != MAX_W)
					{
						minque.push(Edge(i, j, _edges[i][j]));
					}
				}
		
			// 选边
			size_t size = 0; // 是否满足生成树条件
			W totalW = W();
			UnionFindSet ufs(n);

			while (!minque.empty())
			{
				auto min = minque.top();
				minque.pop();
				if (!ufs.isSet(min._srci, min._dsti))
				{
					minTree._AddEdge(min._srci, min._dsti, min._w);
					ufs.Union(min._srci, min._dsti);
					size++;
					totalW += min._w;
				}
			}
			if (size == n - 1) return totalW;
			else return W();
		}

Prim算法：

		W Prim(Self& minTree, const V& vv)
		{
			size_t srci = getVertexIndex(vv);

			// 进行初始化
			int n = _vertex.size();
			minTree._vertex = _vertex;
			minTree._tablemap = _tablemap;
			minTree._edges.resize(n);
			for (int i = 0;i < n;++i)
				minTree._edges[i].resize(n,MAX_W);
			
			// 以vv作为顶点纳入minqueue
			priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
			// 将与vv有关的边加入队列
			for (int i = 0;i < n;++i)
				if (_edges[srci][i] != MAX_W)
					minque.push(Edge(srci, i, _edges[srci][i]));

			// 开始选边
			size_t size = 0; // 记录选择的边数 n - 1 结束
			W totalW = W();   // 按照这个方式选择的边权数

			// 生成树其本质就是一种树形结构
			// 判断一个子图是否构成回路 即看它能否通过某条路径回到原点
			vector<int> start(n, false);
			vector<int> end(n, true);
			start[srci] = true; // 作为起点开始
			end[srci] = false; // 不会作为终边

			while (!minque.empty())
			{
				auto min = minque.top();
				minque.pop();

				// 现在是以dsti 作为顶点 是否被访问过
				if (!start[min._dsti]){
					// 选择出了一条边min
					minTree._AddEdge(min._srci, min._dsti, min._w);
					// 注意这里需要更新 desi!
					start[min._dsti] = true;
					end[min._dsti] = false; // 自己不能再称为ends

					size++;
					totalW += min._w;
					if (size == n - 1) break;
				
					// 将新纳入的顶点 dsti 关联边也纳入
					for (int i = 0;i < n;++i)
					{
						// 该边必须存在 且这个顶点不能是 作为作为终点的！
						if (_edges[min._dsti][i] != MAX_W && end[i])
						{
							minque.push(Edge(min._dsti, i, _edges[min._dsti][i]));
						}
					}
				}
				else {
					// ... 不构成边 ...
				}
			}

			if (size == n - 1) return totalW;
			else return W();
		}

最短路径

最短路径算法	Dijstrak	Bellman-ford	Floyd-warshall
时间复杂度	O(n^2)	O(e*n)	O(n^3)
空间复杂度	O(m)	O(m)	O(n^2)
适用情况	稠密图	稀疏图(暴力更新边)	稠密图
负权	存在负权问题	无	无

Dijkstra算法:

几个问题:

🎨 我们需要从除S集合内以外的点中，找到最短边，是不是仍然可以使用优先级队列帮我们完成这部分排序？

使用优先级队列当然能为我们在选取阶段，一定能选到 ”边值最小边“，但我们最终是通过选“顶点”来规划处 “最短路径”。优先级队列首要的缺陷就在于其不能 ”随意(random)访问“，后面还会牵涉到更新最小路径重新建堆等问题，优先级队列在这里并不适用~

所以，我们使用vector来保存顶点到顶点的最短路径值，使用直接映射的方式，使得我们在更细最短路径值时，也会变得十分简单~

🎨 更新出最短路径值就好了吗？我咋知道你更新的结果是否正确呢？换言之，我们需要去记录最短路径 —— 到底过了哪些顶点。

我们同样采用vector数组，顶点与下标直接映射的方式，每一个位置保存着前驱下标。所以，我们能看到最终更新出的结果，该路径数组是倒序的。

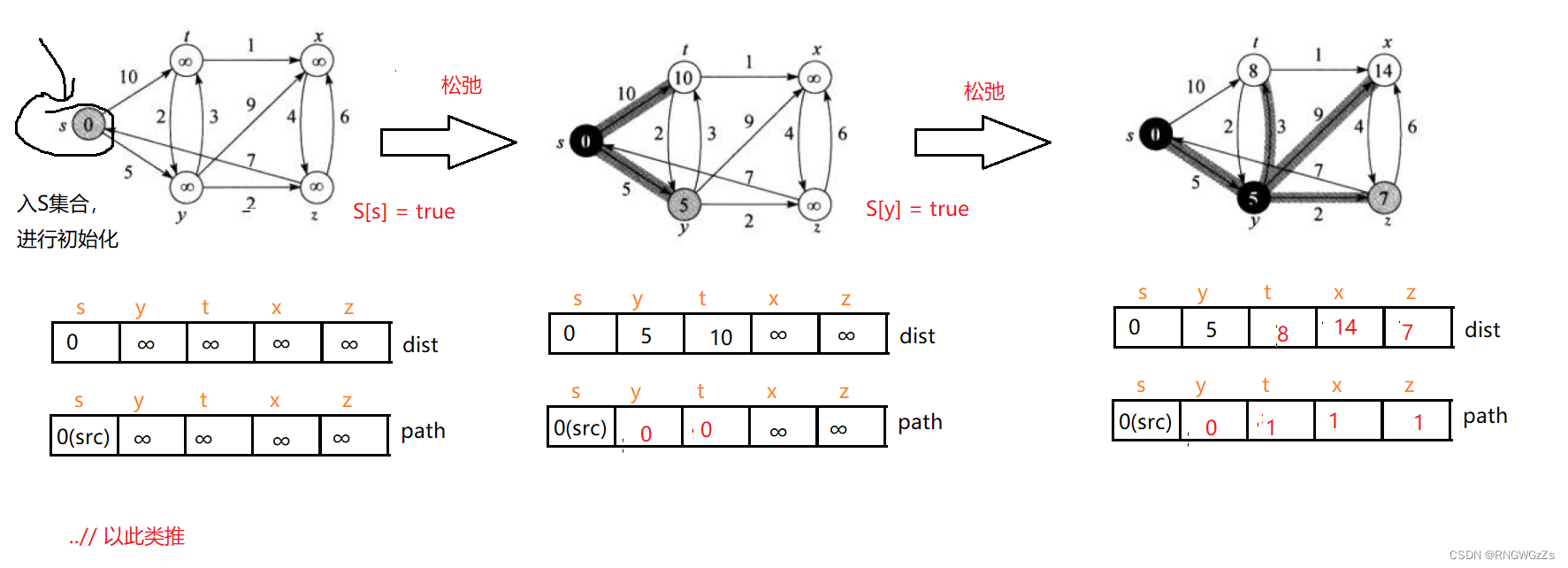
		void DijKstra(const V& vv, vector<W>& distance, vector<int>& path)
		{
			size_t n = _vertex.size();
			size_t srci = getVertexIndex(vv);
			distance.resize(n,MAX_W);	// 最短路径集
			path.resize(n, -1);		// 记录路径
			vector<bool> S(n, false); // 纳入集合中的点
		
			// 进行初始化
			distance[srci] = 0; // 以srci为起点
			path[srci] = srci;

			// 遍历j个顶点
			for (size_t j = 0;j < n;++j)
			{
				// 进行归纳
				int u = 0; // 要纳入的顶点
				W min = MAX_W; // 每次选取最小边
				for (size_t i = 0;i < n;++i)
				{
					// 首次进入 选取的u == srci
					if (S[i] == false && distance[i] < min)
					{
						u = i;
						min = distance[i];
					}
				}
				// 纳入集合S
				S[u] = true;

				// 松弛操作
				// 从u开始，朝其未被纳入S集合的 顶点更新最短距离
				for (size_t v = 0;v < n;++v)
				{
					// 该点是没被纳入集合S的  && 该顶点与u是有关联边的 && 它们的当前值一定是最小的
					if (S[v] == false && _edges[u][v] != MAX_W && _edges[u][v] + distance[u] < distance[v]) {
						distance[v] = _edges[u][v] + distance[u];
						// 记录路径
						path[v] = u;  // 从u->v
					}
				}
			}
		}

当Dijkstra遇到负权路径时，就可能发生失效~

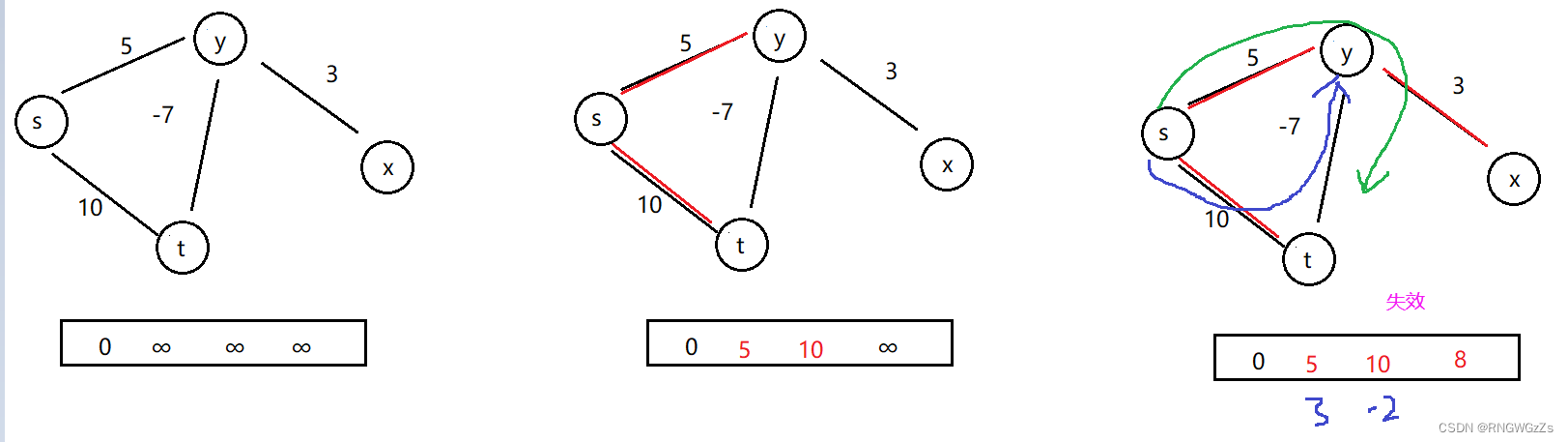
Bellman-ford算法:

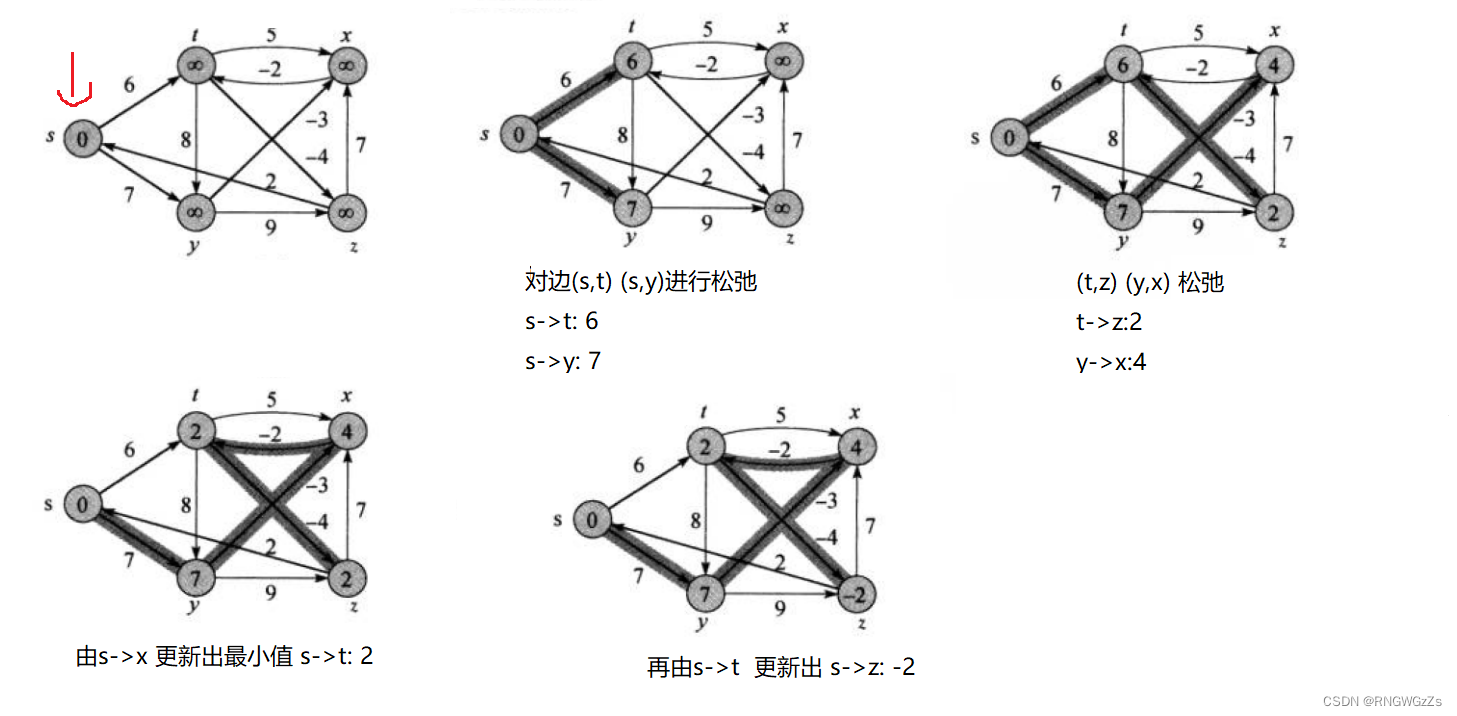
Bellman-ford每次循环都会对有向图G内的所有顶点进行权值更新。每次循环迭代都不一样，所以需要更新多次~

		bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
		{
			size_t n = _vertex.size();
			size_t srci = getVertexIndex(src);
			dist.resize(n, MAX_W);
			pPath.resize(n, -1);

			// 初始化
			dist[srci] = W(); // 给定一个初始值
			// 现在不用记录更新哪些顶点 因为每个顶点都得更新！
			for (int k = 0;k < n;++k)
			{
				// 性能优化 如果不发生更新 说明已经更新完成了 不必再循环了
				bool update = false;

				// 以每一个顶点作为 srci进行遍历
				// i --> j
				for (size_t i = 0; i < n; ++i)
				{
					for (size_t j = 0;j < n;++j)
					{
						if (_edges[i][j] != MAX_W && _edges[i][j] + dist[i] < dist[j]) {
							// 满足min 进行更新
							update = true;
							dist[j] = _edges[i][j] + dist[i];
							pPath[j] = i;
						}
					}
				}
				if (update == false) break;
			}
		
			// 判断负权回路
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
                    // 存在负权回路是没有最短路径的 其会一直更新~
					if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
					{
						return false;
					}
				}
			}
			return true;
		}

Floyd-warshall算法:

		void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
		{
			size_t n = _vertex.size();
			vvDist.resize(n);
			vvpPath.resize(n);

			// 初始化
			for (size_t i = 0; i < n; ++i)
			{
				vvDist[i].resize(n, MAX_W);
				vvpPath[i].resize(n, -1);
			}

			// 更新直接相连的边
			for (size_t i = 0;i < n;++i)
			{
				for (size_t j = 0;j < n;++j)
				{
					if (_edges[i][j] != MAX_W)
					{
						vvDist[i][j] = _edges[i][j];
						vvpPath[i][j] = i;
					}
				}
			}

			// 动态规划 假设k个转点
			for (size_t k = 0; k < n; ++k)
			{
				for (size_t i = 0; i < n; ++i)
				{
					for (size_t j = 0; j < n; ++j)
					{
						if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W &&
							vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
						{
							vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
							// (i,j) 作为子节点 由 [k][j] 进行遍历
							vvpPath[i][j] = vvpPath[k][j];
						}
					}
				}
			}
		}