2012年认证杯SPSSPRO杯数学建模

A题 蜘蛛网

原题再现：

  第二阶段问题
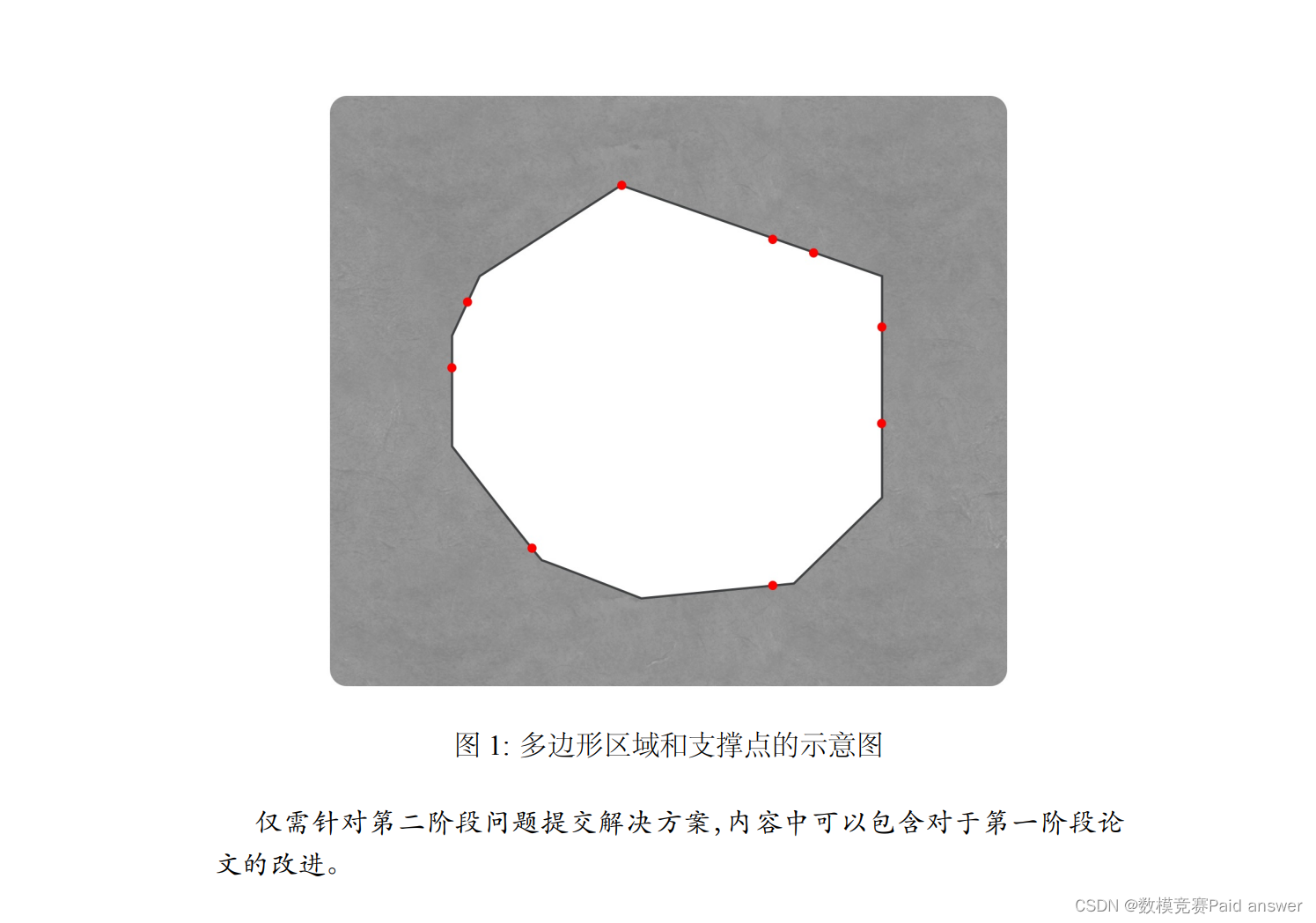
  现在我们假设一个具体的环境。假设有一个凸多边形的区域，蜘蛛准备在这个区域（或其一部分）上结一张网。
  问题一： 在区域的边界上安置有若干支撑点，蛛丝可以连结在支撑点上，不能连结到区域边界的其它点1。请建立合理的数学模型，对不同的情况都设计出合适的蛛网结构。
  问题二： 如果蛛丝可以连结在区域边界的任何点上，请建立合理的数学模型，设计出合适的蛛网结构。

整体求解过程概述(摘要)

  在第二阶段中，我们小组对第一阶段论文进行补充，通过蛛网对数螺旋线模型与圆的比较总结出蛛网的对数螺旋线模型更适合蛛网结构， 又圆与蛛网对数螺旋线模型相类似，所以在此基础上以圆网进行第二阶段问题的研究。通过分析可知：令支撑点在某一区域的边上（所有点不在同一边上） ，对已有区域进行切割或填补即可获得新区域，所以我们小组忽略区域的影响，着重研究支撑点对蛛网结构的影响。
  在平面直角坐标系中用产生随机数算法得到支撑点，将所得支撑点相连即得到一个凸多边形。对凸多边形稳定性进行分析，得出三角形结构最稳定，在研究三角形内置圆最大面积和内角关系并三角形架构上建造圆形蜘蛛网的基础上推导讨论出凸多边形内置圆最大面积和内角关系并在凸多边形架构上建造圆形蜘蛛网。基于以上结论对问题进行分析：
  问题一：用产生随机数算法得到支撑点设计蛛网模型，在平面直角坐标系中做出支撑点所围成的凸多边形内置圆，并在此基础上做出蛛网模型。通过对几组情况的结果的比较得出结论，得到合适的蛛网结构。
  问题二：通过对凸多边形稳定性和三角形内置圆情况的分析得：三角形结构最稳定并在三角形为正三角形的情况下三角形内置圆面积最大。因此，我们小组在区域中任意选取支撑点构成正三角形， 并在取得最大正三角形的情况下载三角形构架上建造蜘蛛网得到在给定区域内的最稳定且捕食面积最大的蛛网模型图。本模型在mathematica8.0.4环境下，对数据进行统一分析等处理，在visualstadio C++6.0编译环境下得到产生随机数算法（源代码见附录） ，从而得出在不同支撑点蜘蛛结出的蛛网的适合结构。

问题分析：

  选取n(n>=3)个支撑点，这n个支撑点在某一区域的边上（n个点不同在一条边上） ，对已知区域进行切割或填补（不把支撑点切割掉）即可获得新的凸多边形区域。所以可以通过讨论一个区域上的情况来代替其他区域的情况，而着重讨论支撑点的选取对蛛网结构的影响来找出合适的蛛网结构。将区域放置于平面直角坐标系中，用产生随机数的算法得出支撑点的坐标，将随机得到的支撑点连接起来即可得到一个凸多边形， 通过对凸多边形稳定性的讨论得出在某个具体区域上适合的蛛网结构。

模型假设

  1.一切统计数据，结构图都要排除极端因素（如自然灾害）的影响；
  2.不考虑药物，杀虫剂等人为因素的影响；
  3.模型中的统计数据及蛛网结构图暂不考虑时间影响；
  4.假设蜘蛛网上所有粘丝力学性质完全相同， 不会因为个别粘丝造成蜘蛛网的断裂；
  5.假设蛛网结构是对称的；

论文缩略图：

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

#include<math.h> 
#include <limits.h> 
#include <windows.h> 
using namespace std; 
class TRandom 
{  public:
TRandom (long seed=0) 
{mSeed=(seed?seed: GetTickCount()); } 
void Seed(long seed=0) 
{mSeed=(seed?seed: GetTickCount());} 
int  Integer() 
{return Next();} 
int  Integer(int min,int max) 
{return min+Next()%(max­min+1);} 
double Real() 
{return double(Next())/double(INT_MAX);} 
private: 
void Change() 
{mSeed=(314159265*mSeed+13579)%ULONG_MAX;} 
int  Next() 
{ int loops=mSeed%3; 
for (int i=0;i<=loops;i++) 
Change (); 
return int (mSeed/2); } 
unsigned long  mSeed; 
}; 
int main() 
{ 
TRandom rand; 
int i=rand.Integer(); 
int a[10],b[10],c[10]; 
int j=0; 
for(i%3;i>0;i­­) 
{ 
a[j]=rand.Integer(3,9); 
j++; 
} 
int i=rand.Integer(); 
int j=0; 
for(i%3;i>0;i­­) 
{ 
b[j]=rand.Integer(3,9); 
j++;

} 
int i=rand.Integer(); 
int j=0; 
for(i%3;i>0;i­­) 
{ 
c[j]=rand.Integer(3,9); 
j++; 
} 
char *pt[]={"A","B","C","D","E","F","G","H","G","I"}; 
cout<<"第一次随机产生的结果："<<endl; 
for(i=o;i<10;i++) 
cout<<pt[a[i]]<<" "; 
cout<<endl; 
cout<<"第二次随机产生的结果："<<endl; 
for(i=o;i<10;i++) 
cout<<pt[b[i]]<<" "; 
cout<<endl; 
cout<<"第三次随机产生的结果："<<endl; 
for(i=o;i<10;i++) 
cout<<pt[c[i]]<<" "; 
cout<<endl; 
return 0; 
}

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可