目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
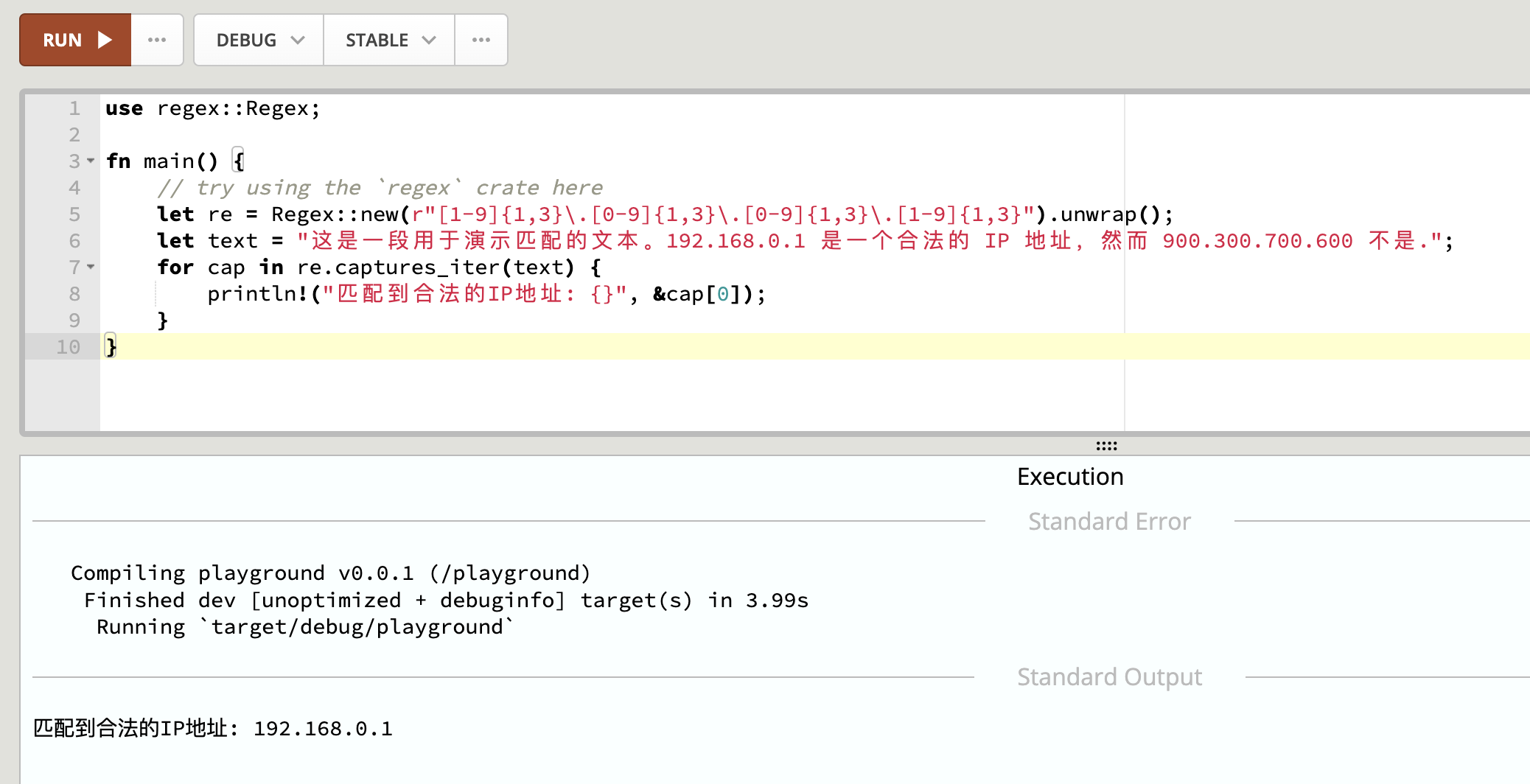
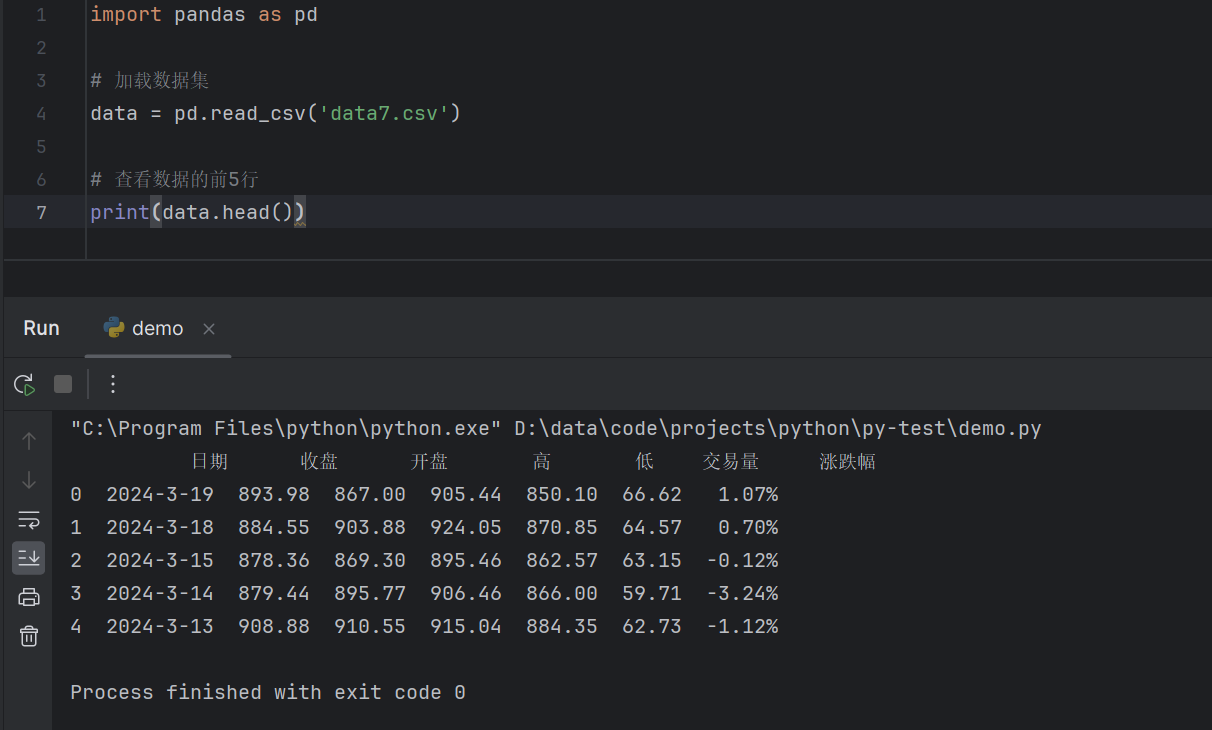
- 3.代码展示
- 4.参考文献
1.背景
2021年,Xie等人受到自然界中金枪鱼狩猎行为启发,提出了金枪鱼优化算法(Tuna swarm optimization,TSO)。
2.算法原理
2.1算法思想
TSO模拟了金枪鱼觅食行为,主要分为螺旋式觅食和抛物线觅食两种方式。
2.2算法过程
螺旋式觅食:
当目标难以锁定时,金枪鱼就会以密集的螺旋式阵型进行追捕。在追捕猎物的同时,金枪鱼群之间还会交换信息,实现相邻个体之间的信息共享。位置更新:
X
i
t
+
1
=
{
c
1
(
X
b
e
s
t
t
+
β
∣
X
b
e
s
t
t
−
X
i
t
∣
)
+
c
2
X
i
t
,
i
=
1
c
1
(
X
b
e
s
t
t
+
β
∣
X
b
e
s
t
t
−
X
i
t
∣
)
+
c
2
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
(1)
X_i^{t+1}=\begin{cases}\quad c_1\left(X_\mathrm{best}^t+\beta\left|X_\mathrm{best}^t-X_i^t\right|\right)+c_2X_i^t,\quad i=1\\c_1\left(X_\mathrm{best}^t+\beta\left|X_\mathrm{best}^t-X_i^t\right|\right)+c_2X_{i-1}^t,\quad i=2,3,\cdots,N\end{cases}\tag{1}
Xit+1={c1(Xbestt+β∣Xbestt−Xit∣)+c2Xit,i=1c1(Xbestt+β∣Xbestt−Xit∣)+c2Xi−1t,i=2,3,⋯,N(1)
c1,c2为权重系数,表述为:
c
1
=
a
+
(
1
−
a
)
t
t
m
a
x
c
2
=
(
1
−
a
)
−
(
1
−
a
)
t
t
m
a
x
β
=
e
b
l
cos
(
2
π
b
)
l
=
e
3
cos
(
(
(
t
max
+
1
/
t
)
−
1
)
π
)
(2)
c_{1}=a+(1-a)\frac{t}{t_{\mathrm{max}}}\\ c_{2}=(1-a)-(1-a)\frac{t}{t_{\mathrm{max}}}\\ \beta=\mathrm{e}^{bl}\cos(2\pi b)\\ l=\mathrm{e}^{3\cos(((t_{\max}+1/t)-1)\pi)}\tag{2}
c1=a+(1−a)tmaxtc2=(1−a)−(1−a)tmaxtβ=eblcos(2πb)l=e3cos(((tmax+1/t)−1)π)(2)
当最优个体无法找到食物时,在搜索空间中随机生成一个坐标:
X
i
t
+
1
=
{
c
1
(
X
r
a
n
d
t
+
β
∣
X
r
a
n
d
t
−
X
i
t
∣
)
+
c
2
X
i
t
,
i
=
1
c
1
(
X
r
a
n
d
t
+
β
∣
X
r
a
n
d
t
−
X
i
t
∣
)
+
c
2
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
(3)
X_i^{t+1}=\begin{cases}c_1\left(X_{\mathrm{rand}}^t+\beta\left|X_{\mathrm{rand}}^t-X_i^t\right|\right)+c_2X_i^t,i=1\\c_1\left(X_{\mathrm{rand}}^t+\beta\left|X_{\mathrm{rand}}^t-X_i^t\right|\right)+c_2X_{i-1}^t,i=2,3,\cdots,N\end{cases}\tag{3}
Xit+1={c1(Xrandt+β∣Xrandt−Xit∣)+c2Xit,i=1c1(Xrandt+β∣Xrandt−Xit∣)+c2Xi−1t,i=2,3,⋯,N(3)
抛物线型觅食:
金枪鱼两种觅食方法交替使用,以提高金枪鱼捕获食物的概率假,设这两种方法随机选择概率为50%:
X
i
t
+
1
=
{
X
b
e
s
t
t
+
r
a
n
d
(
X
b
e
s
t
t
−
X
i
t
)
+
T
F
⋅
p
2
(
X
b
e
s
t
t
−
X
i
t
)
,
i
f
r
a
n
d
<
0.5
T
F
⋅
p
2
X
i
t
,
i
f
r
a
n
d
⩾
0.5
,
(4)
X_i^{t+1}=\begin{cases}X_\mathrm{best}^t+rand\left(X_\mathrm{best}^t-X_i^t\right)+TF\cdot p^2\left(X_\mathrm{best}^t-X_i^t\right),\quad ifrand<0.5\\TF\cdot p^2X_i^t,\quad if rand\geqslant0.5\end{cases},\tag{4}
Xit+1={Xbestt+rand(Xbestt−Xit)+TF⋅p2(Xbestt−Xit),ifrand<0.5TF⋅p2Xit,ifrand⩾0.5,(4)
参数p表述为:
p
=
(
1
−
t
t
max
)
(
t
/
t
max
)
(5)
p=(1-\frac{t}{t_{\max}})^{(t/t_{\max})}\tag{5}
p=(1−tmaxt)(t/tmax)(5)
流程图
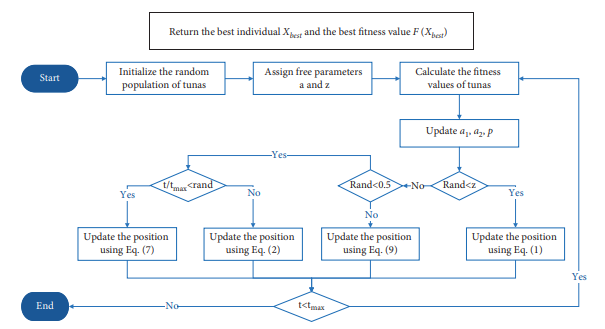
伪代码:

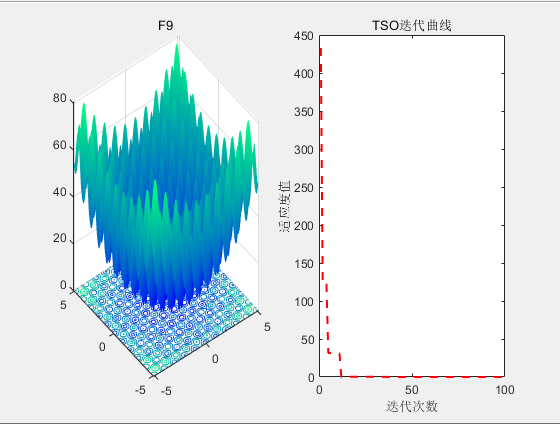
3.代码展示
4.参考文献
[1] Xie L, Han T, Zhou H, et al. Tuna swarm optimization: a novel swarm-based metaheuristic algorithm for global optimization[J]. Computational intelligence and Neuroscience, 2021, 2021: 1-22.