回溯算法 DFS

news2024/11/24 4:37:59

回溯算法和dfs的区别

回溯算法和dfs算法极为相似，本质上就是一种暴力穷举算法。
区别就是：回溯算法是在遍历【树枝】，dfs算法是在遍历【节点】

回溯算法

基本框架

result = []
def backtrack(路径，选择列表）:
	if 满足结束条件:
		result.add(路径)
		return

	for 选择 in 选择列表:
		做选择
		backtrack（路径，选择列表）
		撤销选择

例题：【1,2，3】的全排列

如图，1,2，3的全排列我们可以用一个树来表示（回溯算法是记录路径！！）

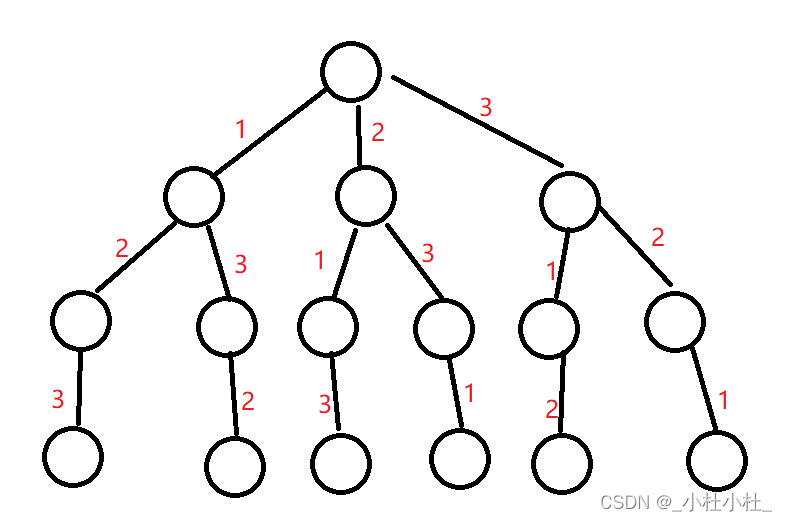
在这里插入图片描述

大致思想是这样的（先拿出来一支杈分析分析）

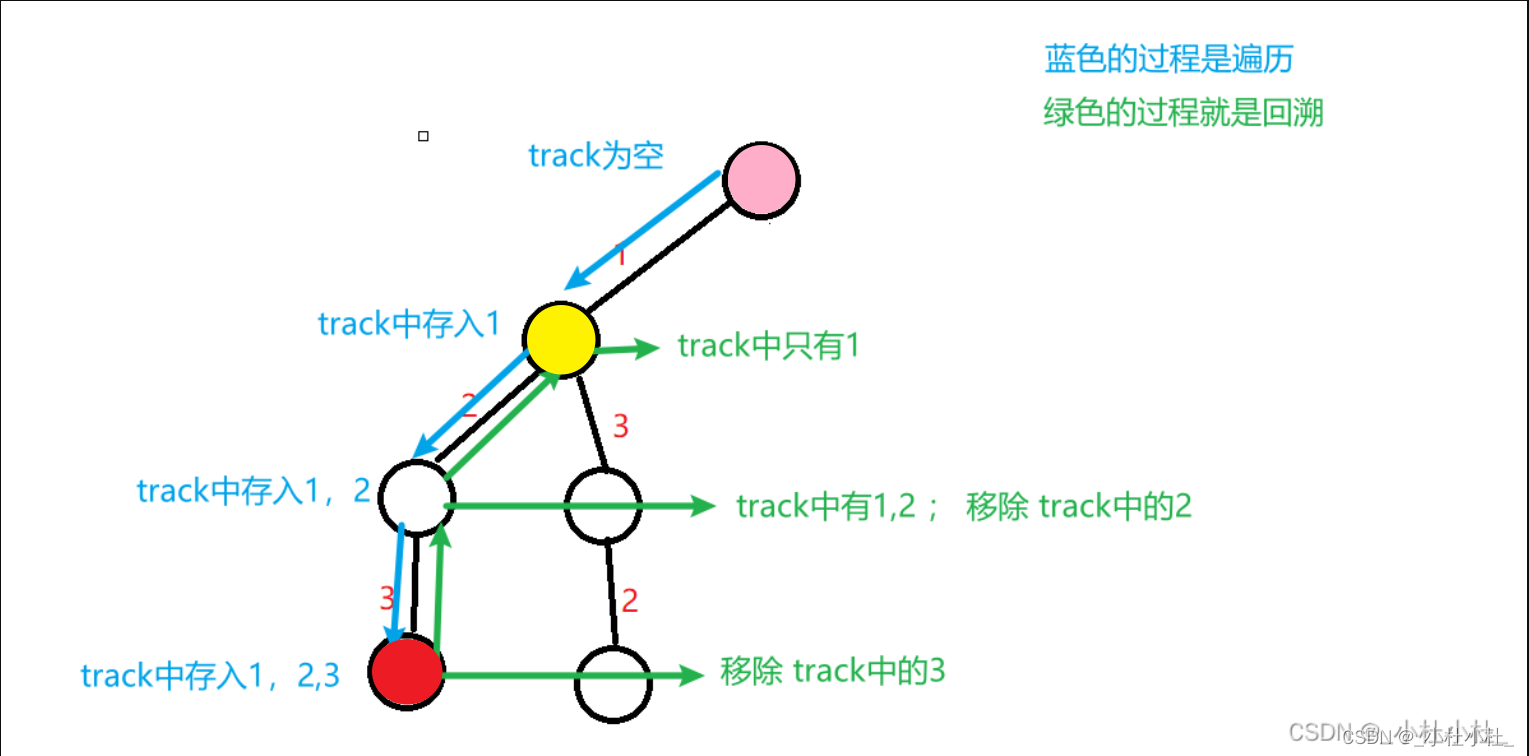
站在一个回溯树的节点上，只需要思考3个问题：
1.路径：也就是已经做出的选择
2.选择列表：也就是当前可以做的选择
3.结束条件：到达决策树底层，无法再做选择的条件

只针对上面有色儿的那一支杈

  - 对于上面的“粉色”节点：
  	路径：没有
  	选择列表：【1】
  	结束条件：遍历到叶子节点
  - 对于上面的“黄色”节点：
  	路径：【1】
  	选择列表：【2,3】
  	结束条件：遍历到叶子节点
  - “红色”：
  	路径：【1,2，3】
  	选择列表：没有
  	结束条件：到达结束条件

代码详解

基本思想完事了，我们来仔细分析下代码

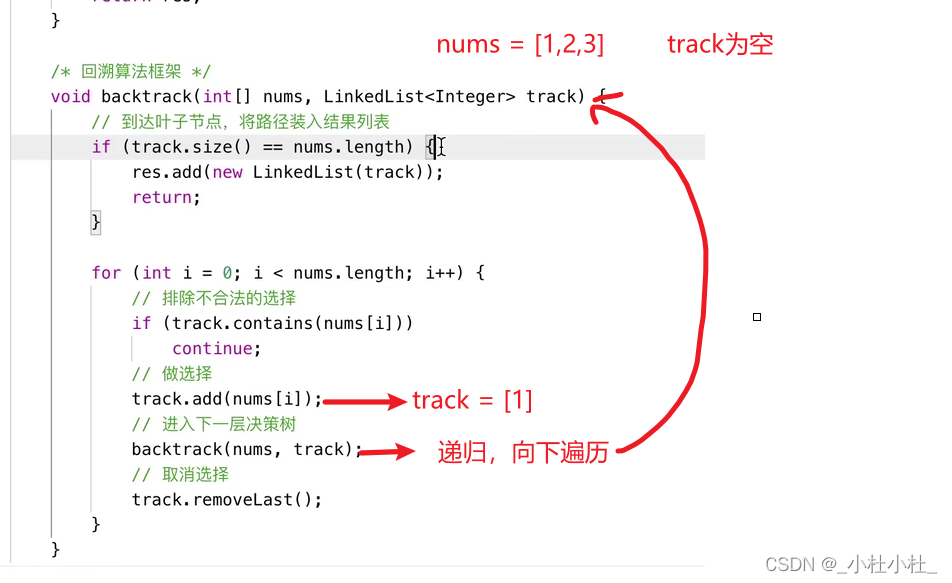
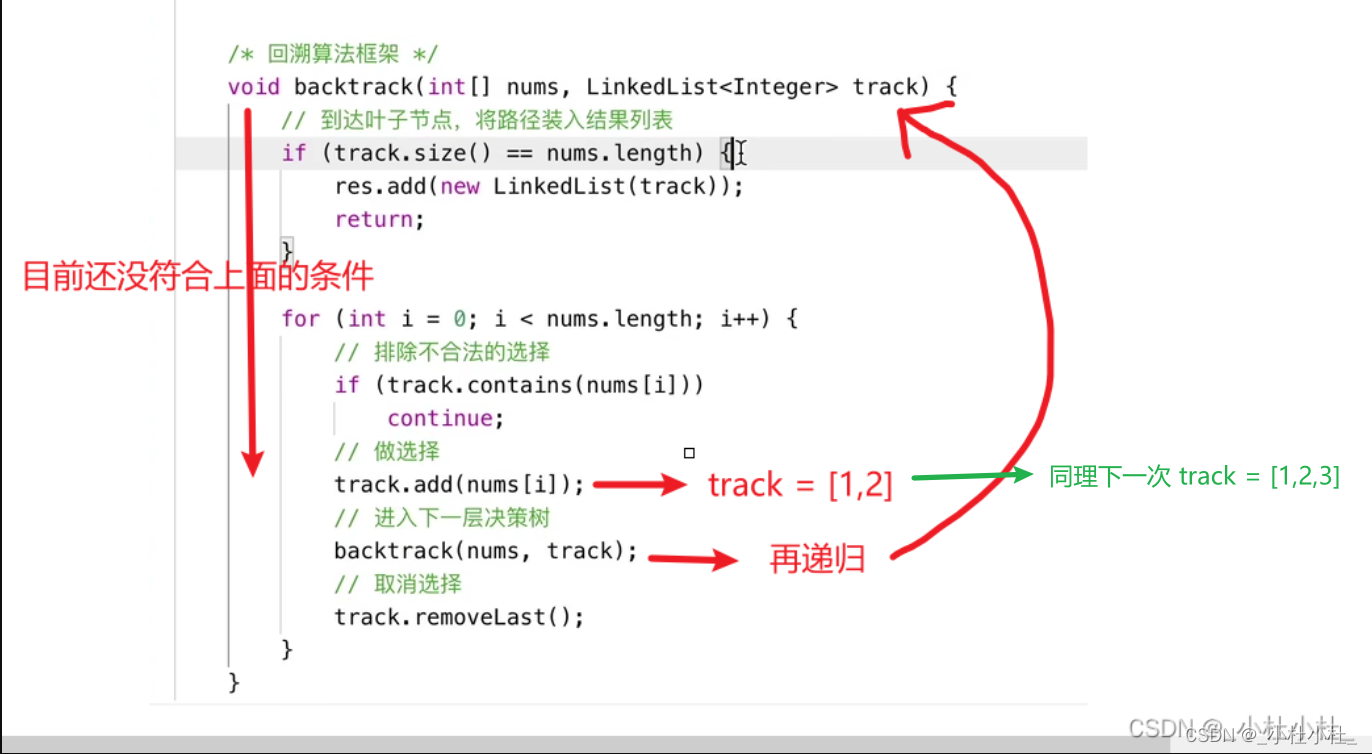
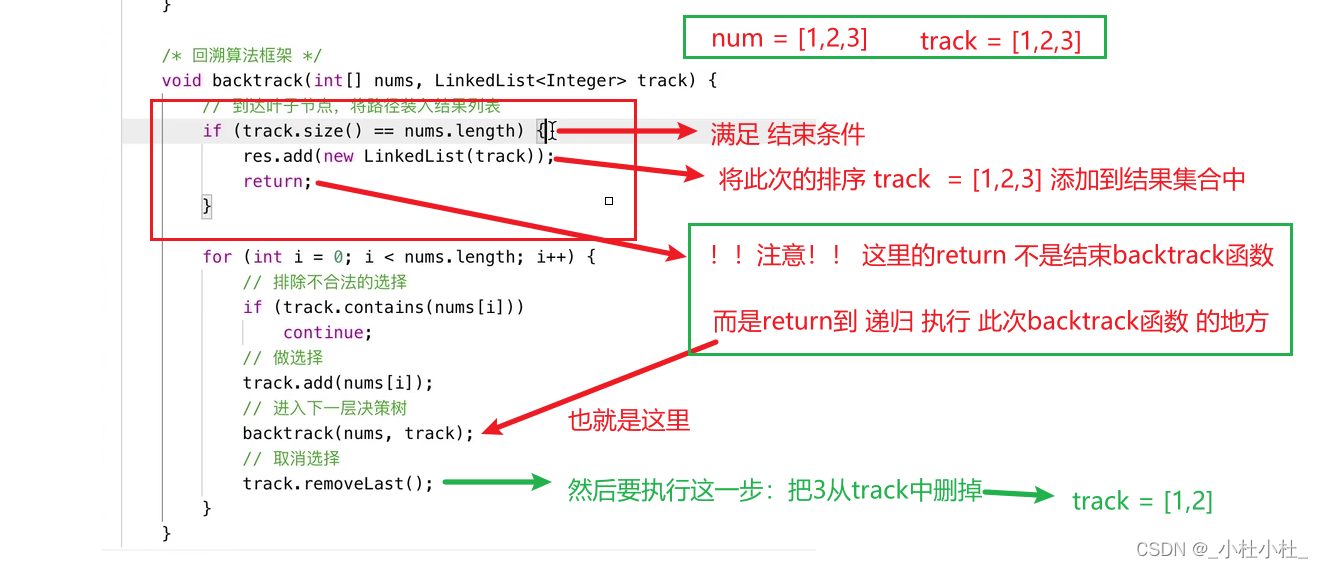
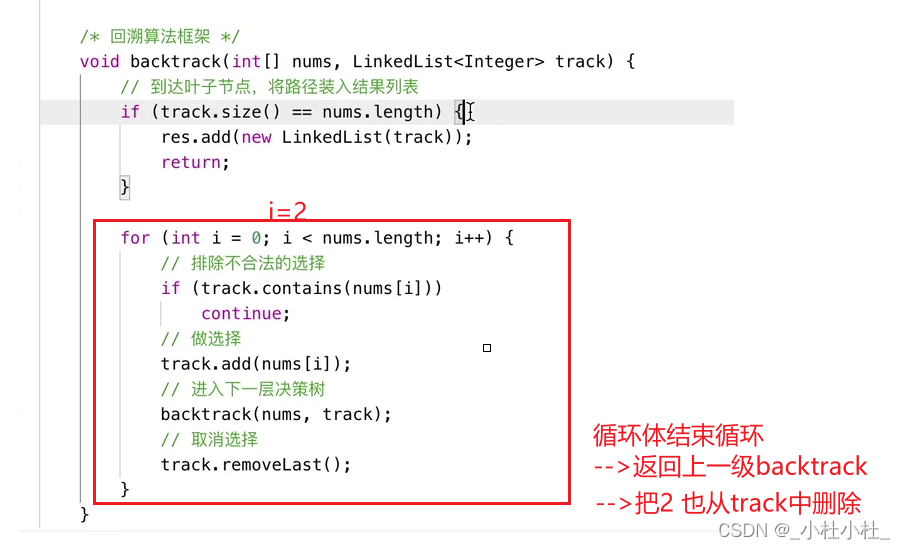
在这里插入图片描述

完整代码

import java.util.LinkedList;
import java.util.List;

//import com.sun.xml.internal.bind.v2.schemagen.xmlschema.List;

public class Main{
	static LinkedList<List<Integer>> list = new LinkedList<>();

	public static void main(String[] args) {
		int[] nums = {1,2,3};
		System.out.println(permute(nums));
	}
	
	//输入一组不重复的数字，返回他们的全排列
	static List<List<Integer>> permute(int[] nums){
		//记录[路径]
		LinkedList<Integer> track = new LinkedList<>();
		// [路径] 中的元素会被标记为true,避免重复使用
		boolean[] used = new boolean[nums.length];
		
		backtrack(nums,track,used);
		return list;
	}

	// 路径:记录在track中
	//选择列表:nums中不存在于track的那些元素(used[i] 为false)
	//结束条件:nums中的元素全都在track中出现
	static void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
		//结束条件
		if(track.size() == nums.length) {
			list.add(new LinkedList(track));
			return;	//返回上一级backtrack
		}
		
		for(int i=0;i<nums.length;i++) {
			//排除不合法的选择
			if(used[i]) {
				//nums[i]已经在track中,跳过
				continue;
			}
			
			//做选择
			track.add(nums[i]);
			used[i] = true;
			//进入下一层决策树
			backtrack(nums, track, used);
			//取消选择
			track.removeLast();
			used[i] = false;
		}
		
		//return;	//返回上一级的backtrack(不加也行,循环结束,自动返回上一级backtrack)
		
	}
}

DFS

我在读这篇<回溯算法>的文章时 , 本以为他会讲回溯算法和dfs的区别但是,文章后面说----其实回溯算法就是dfs…(无语啊啊啊啊)

总的来说,几乎没有区别
下面这个是我之前学过的一个dfs全排列的代码,一起来对比一下吧
详情看这篇文章,也算是看一看另一种理解方式吧
//也是[1,2,3]的全排列

import java.util.Scanner;

public class Main {

    static int n;
    static int[] a;
    static boolean book[];

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        a=new int[n+2];
        book=new boolean[n+2];
        dfs(1);
        scanner.close();
    }
    public static void dfs(int k) {
        // 回头条件
        if(k==n+1){ //说明n个盒子都已经放完了
            for(int i=1;i<=n;i++){
                System.out.print(a[i]+" ");
            }
            System.out.println();
            return; //这里的return是返回上一级dfs（可以理解为，方案一执行完了，还要进行方案二的排序）
        }

        // 放牌等操作
        for(int i=1;i<=n;i++){   //进行1～n号牌的排序
            if(book[i]==false){ //当这个盒子里没有牌时，可以进行以下操作
                a[k]=i;         //i号牌放入k号盒子中
                book[i]=true;   //标记盒子不为空
                dfs(k+1);       //带着手中的牌，走向下一个盒子
                book[i]=false;  //箱子置空。其实每次循环都执行到dfs（k++），只有当执行到没有路可走的时候，才会"回头"；也就相当于例子中的，要从3号箱开始往回一个个收牌了
            }
        }
        return;

    }
}