题目链接
NOIP2014提高组D1T2:联合权值
题目描述
无向连通图 G G G 有 n n n 个点, n − 1 n-1 n−1 条边。点从 1 1 1 到 n n n 依次编号,编号为 i i i 的点的权值为 W i W_i Wi,每条边的长度均为 1 1 1。图上两点 ( u , v ) (u, v) (u,v) 的距离定义为 u u u 点到 v v v 点的最短距离。对于图 G G G 上的点对 ( u , v ) (u, v) (u,v),若它们的距离为 2 2 2,则它们之间会产生 W v × W u W_v \times W_u Wv×Wu 的联合权值。
请问图 G G G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入格式
第一行包含 1 1 1 个整数 n n n。
接下来 n − 1 n-1 n−1 行,每行包含 2 2 2 个用空格隔开的正整数 u , v u,v u,v,表示编号为 u u u 和编号为 v v v 的点之间有边相连。
最后 1 1 1 行,包含 n n n 个正整数,每两个正整数之间用一个空格隔开,其中第 i i i 个整数表示图 G G G 上编号为 i i i 的点的权值为 W i W_i Wi。
输出格式
输出共 1 1 1 行,包含 2 2 2 个整数,之间用一个空格隔开,依次为图 G G G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对 10007 10007 10007 取余。
样例 #1
样例输入 #1
5
1 2
2 3
3 4
4 5
1 5 2 3 10
样例输出 #1
20 74
提示
样例解释
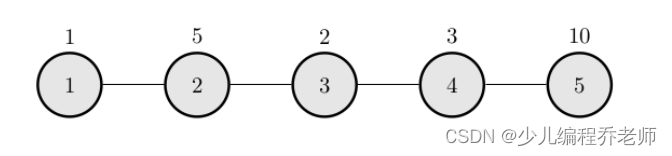
本例输入的图如上所示,距离为 2 2 2 的有序点对有 ( 1 , 3 ) (1,3) (1,3) 、 ( 2 , 4 ) (2,4) (2,4) 、 ( 3 , 1 ) (3,1) (3,1) 、$(3,5) 、 、 、(4,2)$ 、$(5,3) $。
其联合权值分别为 2 , 15 , 2 , 20 , 15 , 20 2,15,2,20,15,20 2,15,2,20,15,20。其中最大的是 20 20 20,总和为 74 74 74。
数据说明
- 对于 30 % 30\% 30% 的数据, 1 < n ≤ 100 1 < n \leq 100 1<n≤100;
- 对于 60 % 60\% 60% 的数据, 1 < n ≤ 2000 1 < n \leq 2000 1<n≤2000;
- 对于 100 % 100\% 100% 的数据, 1 < n ≤ 2 × 1 0 5 1 < n \leq 2\times 10^5 1<n≤2×105, 0 < W i ≤ 10000 0 < W_i \leq 10000 0<Wi≤10000。
保证一定存在可产生联合权值的有序点对。
算法思想
根据题目描述,无向连通图
G
G
G 有
n
n
n 个点,
n
−
1
n-1
n−1 条边,说明该图是一棵树。对于一棵树来说,距离为
2
2
2的点对有下面两种情况,姑且称为“一字形”和“八字形”:
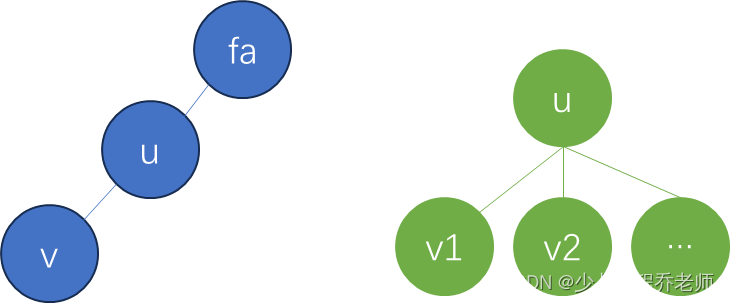
对于一字形来说,
f
a
fa
fa和
v
v
v之间的联合权值为
W
f
a
×
W
v
W_{fa} \times W_v
Wfa×Wv ,可以直接求其中的最大值和所有联合权值之和。
对于八字型来说,可以将当前节点
u
u
u的所有子节点
v
1
,
v
2
.
.
.
v_1,v_2...
v1,v2...两两配对,求其中的最大值和所有联合权值之和。由于每个点的权值
W
i
>
0
W_i>0
Wi>0,因此可以维护一个前缀最大值pre_max和前缀和pre_sum。这样每一点线性扫描一遍即可,不需要
O
(
n
2
)
O(n^2)
O(n2) 枚举。
值得注意的是 ( u , v ) (u, v) (u,v)和 ( v , u ) (v, u) (v,u)是两个不同的点对,因此在计算最终联合权值之和时要乘 2 2 2。
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 200005, mod = 10007;
int w[N], ans_max, ans_sum;
vector<int> g[N];
void dfs(int u, int fa)
{
int pre_max = 0, pre_sum = 0; //前缀最大值,前缀和
for(int v : g[u])
{
if(v == fa) continue;
if(fa != -1) //一字型
{
ans_max = max(ans_max, w[v] * w[fa]);
ans_sum = (ans_sum + w[v] * w[fa]) % mod;
}
//八字形
ans_max = max(ans_max, w[v] * pre_max);
ans_sum = (ans_sum + w[v] * pre_sum) % mod;
//更新前缀最大值和前缀和
pre_max = max(pre_max, w[v]);
pre_sum = (pre_sum + w[v]) % mod;
dfs(v, u);
}
}
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i < n; i ++) //n个点树有n-1条边
{
int u, v;
scanf("%d%d", &u, &v);
g[u].push_back(v), g[v].push_back(u); //无向图,双向建边
}
for(int i = 1; i <= n; i ++) scanf("%d", &w[i]);
dfs(1, -1);
printf("%d %d", ans_max, ans_sum * 2 % mod);
return 0;
}