C++算法——二分法查找

news2024/11/25 12:55:50

一、二分查找算法思想和模版

1.算法思想

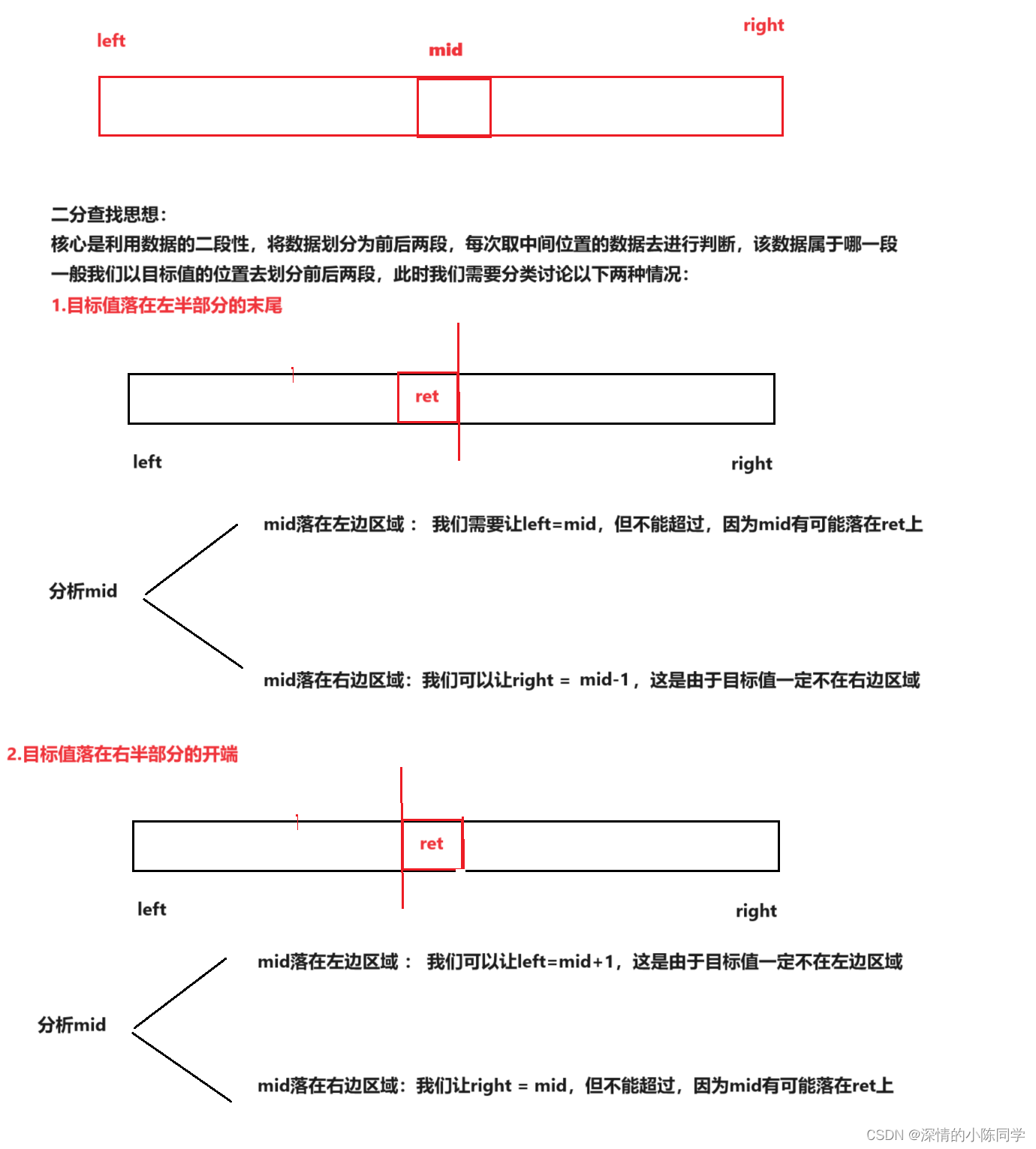
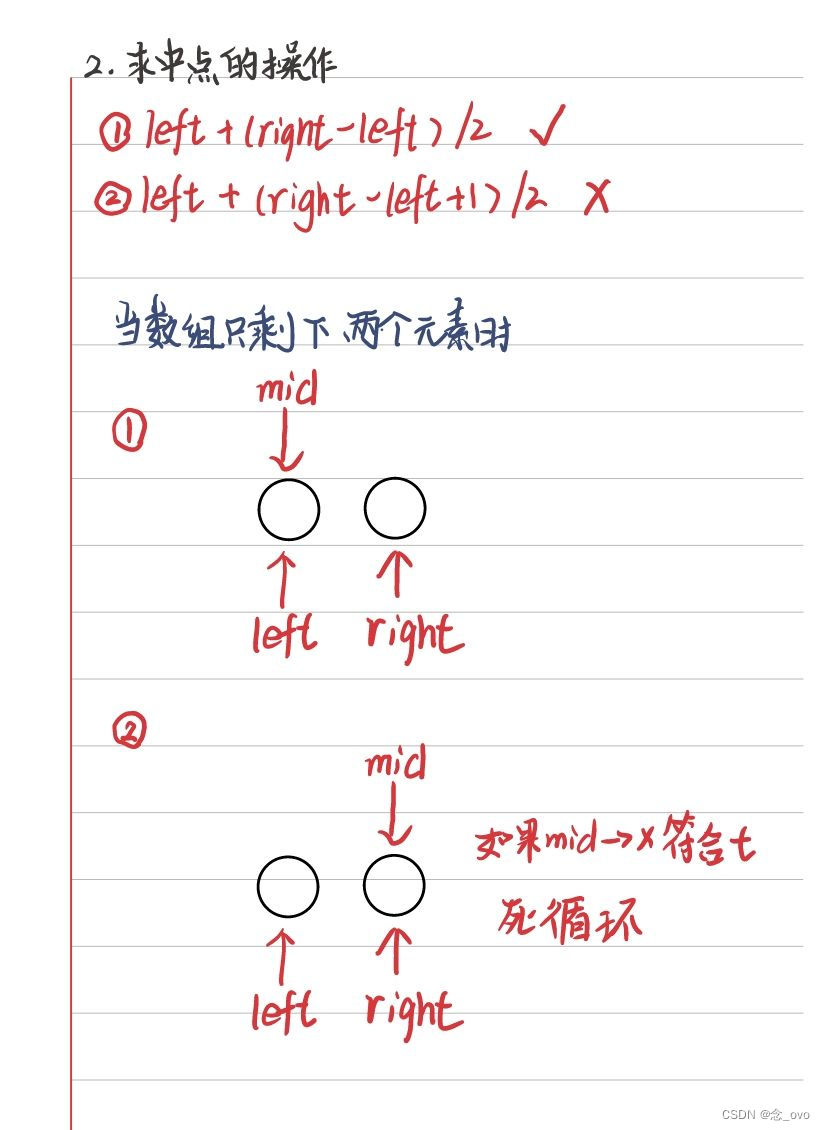
2.细节处理

3.模板

二、二分查找

1.链接

704. 二分查找 - 力扣（LeetCode）

2.描述

3.思路

先从最经典的题目去切入，思路就是二分查找，这里我们认为，目标值既可以看作为左部分的后端，也可以认为是右部分的前端，当然有更简单的写法，就是直接判断相等，但那个方式对二分查找这一类题目的普适性不高，作为练习，我们这里采用目标值落在左边末端的情况

4.参考代码

认为目标值在左边末端的情况

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left+ (right - left + 1)/2;
            if(nums[mid] <= target)
            {
                left = mid;
            }
            else
            {
                right = mid-1;
            }
        }
        if(nums[left] == target) return left;
        else return -1;
    }
};

三、在排序数组中查找元素的第⼀个和最后⼀个位置

1.链接

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

2.描述

3.思路

通过分析，这题我们需要找到target的开始和末尾，我们可以分别进行两次二分查找去分别找到开端和末尾，刚好对应着两种不同的策略和模版

target开端：我们将数据划分成【小于target的数】【target开端 和大于等于target的数】，此时目标数据在后半段的开端

target后端：数据划分成【小于等于target的数，target末尾】【大于target的数】，此时目标值在前半段的末端

当然也要考虑不存在target的情况，在第一次找开端时，若是没找到，则可以直接返回{-1，-1}

4.参考代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        //由于有空数组，做个特殊处理
        if(nums.size() == 0)
        {
            return {-1,-1};
        }

        //寻找target开端
        int begin,end;
        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        if(nums[left] == target) begin = left;
        else return {-1,-1};

        //寻找target末尾
        right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right - left + 1)/2;
            if(nums[mid] <= target) left = mid;
            else right = mid - 1;
        }
        //由于开端已经找到，则说明一定存在target，末端也一定存在
        end = left;
        return {begin,end};
    }
};

四、搜索插入位置

1.链接

35. 搜索插入位置 - 力扣（LeetCode）

2.描述

3.思路

根据题意，我们不能看出使用二分查找的方法，根据题目意思，有两种情况

一种是目标值存在，那么和最简单的二分查找找目标值那题是一样的，采用哪种策略划分都可以

另一种是不存在则返回插入位置的索引，这个插入位置的索引原先是比target较大一点的值

因此我们将区域划分为【小于target的值】【大于等于target的值】，此时我们要找到目标索引就是后半部分的开端

此外，还需要考虑边界情况：

1.数组内的数全都大于target

最终，right在不断调整下，会落在0上，是满足题意的

2.数组内的数全都小于target

最终，left会落在right（最后一个位置的索引），但实际要求插入的位置是right+1的地方

所以这里做一个判断，若是最终出来的值小于target，则返回right+1（left+1）

4.参考代码

class Solution 
{
public:
    int searchInsert(vector<int>& nums, int target) 
    {
        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(nums[mid] < target) left = mid + 1;
            else right = mid; 
        }
        if(nums[left] < target) left++;
        return left;
    }
};

五、x的平方根

1.链接

69. x 的平方根 - 力扣（LeetCode）

2.描述

3.思路

根据题意，我们可以认为，目标值的范围，一定会是在【1，x】区间，我们根据这个区间内每个数的平方去划分前后两个区间【平方小于等于x的数】【平方大于x的数】，我们要找的目标值落在前半部分区间的末端

考虑边界情况，目标值一定会存在，但是x从0开始，因此，我们需要对x=0时的情况做一个特殊处理

4.参考代码

class Solution {
public:
    int mySqrt(int x) 
    {
        if(x == 0) return 0;
        int left = 1;
        int right = x;
        while(left < right)
        {
            long long mid = left + (right - left + 1)/2;
            if(mid*mid <= x) left = mid;
            else right = mid - 1;
        }
        return left;
    }
};

六、山脉数组的峰值索引

1.链接

852. 山脉数组的峰顶索引 - 力扣（LeetCode）

2.描述

3.思路

通过题意，我们可以将数据划分为这两种情况【前半部分都是递增的数据】【后半部分全是递减的数据】，我们要找到目标值，可以认为是在前半部分的末端，也可以认为是后半部分的开端，任选一个即可

由于题目说一定是山峰数组且数组长度大于等于3，因此可以不考虑特殊情况

这题需要稍微分析的就是条件的判断：

若是认为目标值在前半段的末端，则在判断递增还是递减时，则需要前一个比较后一个

若是认为目标值在后半段开端，则判断递增还是递减时，需要后一个比较前一个

4.参考代码

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) 
    {
        int left = 0;
        int right = arr.size()-1;
        while(left<right)
        {
            int mid = left + (right - left + 1)/2;
            if(arr[mid] > arr[mid-1]) left = mid;
            else right = mid -1;
        }
        return left;
    }

七、寻找峰值

1.链接

162. 寻找峰值 - 力扣（LeetCode）

2.描述

3.思路

只需要找到数组中任意一个峰值即可，因此思路和上一题是一样的

4.参考代码

class Solution {
public:
    int findPeakElement(vector<int>& nums) 
    {

        int left = 0;
        int right = nums.size()-1;
        while(left < right)
        {
            int mid = left + (right - left + 1)/2;
            if(nums[mid] > nums[mid-1]) left = mid;
            else right = mid -1;
        }
        return left;
    }
};

八、搜索旋转排序数组中的最小值

1.链接

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

2.描述

3.思路

4.参考代码

class Solution {
public:
    int findMin(vector<int>& nums) 
    {
        int left = 0;
        int right = nums.size()-1;
        int x = nums[right];
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(nums[mid] > x) left = mid+1;
            else right = mid;
        }
        return nums[left];
    }
};

九、点名

1.链接

LCR 173. 点名 - 力扣（LeetCode）

2.描述

3.思路

根据题意，我们知道，若是没有人缺席，下标和数字应该会严格的一一对应的，我们可以将数据划分为前后两段【下标和元素严格对应】【下标和元素没有对应】，我们的目标值就落在后半段的开端

还需要考虑一下边界条件，若是恰好最后一位同学缺席，此时该算法会算到倒数第二位学号的同学，此时在返回时做一个判断即可

return left == records[left] ? left+1:left ;

4.参考代码

class Solution {
public:
    int takeAttendance(vector<int>& records) 
    {
        
        int left = 0;
        int right = records.size()-1;
        while(left < right)
        {
            int mid = left + (right - left)/2;
            if(records[mid] == mid) left = mid+1;
            else right = mid;
        }
        return left == records[left] ? left+1:left;
    }
};