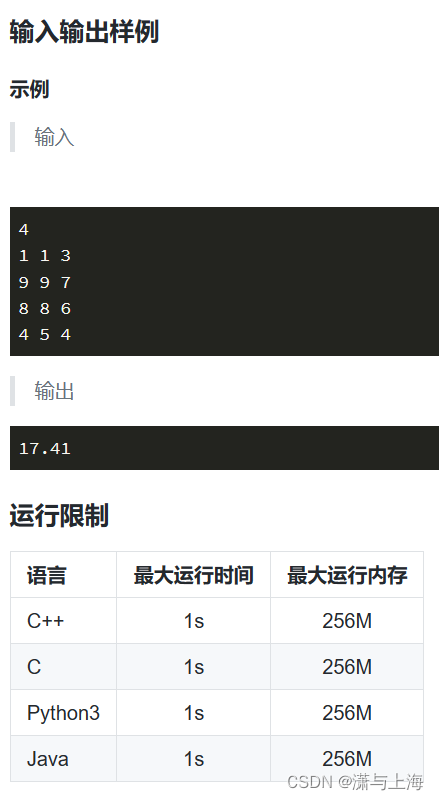
kruskal做法(加边)

#include <bits/stdc++.h>
using namespace std;
int x[10005],y[10005],z[10005];//存储i点的x与y坐标 
int bcj[10005];//并查集 
struct Edge{//边 
    int v1,v2; 
    double w;
}edge[2000005];
int cmp(Edge a, Edge b){return a.w < b.w;}
int find(int x){//并查集查找 
    if(bcj[x]!=x)bcj[x]=find(bcj[x]);//带路径压缩
    return bcj[x];
}
void merge(int v1,int v2){//并查集合并 
    v1=find(v1);v2=find(v2);
    bcj[v2]=v1;
}
int main(){
    //
    int n;cin>>n;
    for(int i=1;i<=n;++i)bcj[i]=i;//并查集初始化
    //
    for(int i=1;i<=n;i++)cin>>x[i]>>y[i]>>z[i];//读取结点x坐标y坐标 
    int cnt=0;
    for(int v1=1;v1<=n;++v1)for(int v2=v1+1;v2<=n;++v2){//求出任意两点的权重 
        double w=sqrt(pow((x[v1]-x[v2]),2)+pow((y[v1]-y[v2]),2))+pow((z[v1]-z[v2]),2);//v1的x坐标减去v2的x坐标... 
        edge[++cnt]={v1,v2,w};
    }
    sort(edge+1,edge+cnt+1,cmp);
    int MSTm = 0;
    double sumw = 0.0;
    //解决了任意孤立点(一个点就是一个集合),然后对每个点作n-1个点的相连边并排序,保证每次取得是最短的,并且使用并查集避免出现环路. 
    //取得边是离散的,总可以取完 
    for(int i=1;i<=cnt;++i){//依次取得边,其权重递增 
        if(find(edge[i].v1)!=find(edge[i].v2)){//若两边端点不属于同一个集合,则合并 
            merge(edge[i].v1,edge[i].v2);//每次取一条边并将其标记为一个集合,使其不出现环路 
            ++MSTm;
            sumprimzuofaw+=edge[i].w;//获取MST中最大的边 
        }
        if(MSTm==n-1)break;//n-1条边就可以构造MST 
    }
    cout<<fixed<<setprecision(2)<<sumw<<endl;
    return 0;
}

prim做法(加点)

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 1005;
vector<int> demo;
double closest[MAXN], lowcost[MAXN];
int m, n;             // m为节点的个数，n为边的数量
double G[MAXN][MAXN]; // 邻接矩阵
double prim()
{
    for (int i = 0; i < m; i++)
    {
        lowcost[i] = INF;
    }
    for (int i = 0; i < m; i++)
    {
        closest[i] = 0;
    }
    closest[0] = -1;             // 加入第一个点，-1表示该点在集合U中，否则在集合V中
    int num = 0,  e = 0; // e为最新加入集合的点
    double ans=0;
    while (num < m - 1)          // 加入m-1条边
    {
        int miedge = -1;
        double micost = INF;
        for (int i = 0; i < m; i++)
            if (closest[i] != -1)
            {
                double temp = G[e][i];
                if (temp < lowcost[i])
                {
                    lowcost[i] = temp;
                    closest[i] = e;
                }
                if (lowcost[i] < micost)
                    micost = lowcost[miedge = i];
            }
        ans += micost;
        demo.push_back(micost);
        closest[e = miedge] = -1;
        num++;
    }
    return ans;
}

struct node
{
    double x, y, h;
} dis[MAXN];

double getDistance(node a, node b)
{
    return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)) + pow(a.h - b.h, 2);
}

int main()
{

    scanf("%d", &m);

    for (int i = 0; i < m; i++)
        scanf("%lf%lf%lf", &dis[i].x, &dis[i].y, &dis[i].h);
    for (int i = 0; i < m - 1; i++)
        for (int j = i + 1; j < m; j++)
        {
            G[i][j] = getDistance(dis[i], dis[j]);
            G[j][i] = G[i][j];
        }

    printf("%.2lf", prim());
    // for (int i = 0; i < m - 1; i++)
    //     cout << demo[i] << " ";
    return 0;
}